Силы, действующие на поезд. Уравнение движения поезда. Режим тяги. Методы интегрирования уравнения движения поезда

1. силы, действующие на поезд.

Поезд представляет систему материальных тел, обладающих упругими и жесткими связями. Материальными телами являются вагоны и локомотивы, упругими связями — междувагонные сцепления, а жесткими — рельсы (без учета их упругости).

Все силы, действующие  на  материальную систему, делятся на внешние   и внутренние. Внешними   силами    называются такие действие которых исходит от тел, не входящих в рассматриваемую систему, а внутренними — силы, действующие на отдельные точки внутри данной материальной системы (или силы взаимодействия между отдельными элементами системы). В поезде внешними по отношению к нему силами будут притяжение земли (вес  езда), реакции, действующие  от рельсов,  и  воздействие среды,   ё, которой движется поезд, в данном случае воздуха,  внутренними же силами будут взаимодействия между отдельными вагонами.

Тогда все действующие на поезд внешние силы можно свести в три группы:

а)  силы, передающиеся от локомотива, т. е. сила тяги F;

б)  силы, оказывающие сопротивление движению подвижного состава (естественные) W;

в)  тормозные силы (искусственное сопротивление) В. Указанные силы действуют в поезде не одновременно, а в одной из следующих комбинаций: силы тяги и силы естественного сопротивления; только силы естественного сопротивления; тормозные силы и силы сопротивления. Равнодействующая одновременно действующих на поезд сил, взятая в направлении его движения, определяет характер и количественные факторы движения.

2. Уравнение движения поезда.

Движение поезда происходит по участку с разнообразным профилем пути, для построения диаграмм ускоряющих сил и анализа по ним характера движения поезда достаточно рассчитать действующие силы для случая движения поезда по прямому горизонтальному пути. Процесс движения поезда по участку характеризуется тремя режимами работы локомотива: тяга, выбег (холостой ход) и торможение

Режим тяги.Применительно к электровозу и тепловозу с электрической передачей режим тяги соответствует движению под током (у паровоза с открытым регулятором). В этом случае движение происходит с работающими тяговыми электродвигателями (паровой машиной) локомотива, и на поезд действуют сила тяги локомотива F_Kи сила основного сопротивления W₀. Равнодействующая этих сил Rопределяется величиной

Режим выбега — движение без тока (с закрытым регулятором). В этом случае движение происходит с выключенными тяговыми электродвигателями (паровой машиной) локомотива, и на поезд действует основное сопротивление W_ox. Равнодействующая сила Rопределяется величиной

Режим торможения. На поезд действуют сила основного сопротивления W_oxи тормозная сила В_т. Равнодействующая этих сил Rопределяется величиной

Характер движения поезда определяется величиной и направлением равнодействующей силы. Если равнодействующая сила R

равна нулю, to имеет место равномерное движение поезда (или стоянка), если больше нуля, — движение ускоренное, если меньше нуля, — движение замедленное.

3. Методы интегрирования уравнения движения

Поезда

Аналитическое интегрирование уравнения движения поезда. Интегрирование уравнения движения поезда позволяет найти зависимость между скоростью и, временем tи пройденным расстоянием s.

Разделив переменные в уравнении движения, получим

Интегрируя  обе  части  этого уравнения  в  пределах  изменения :корости от Vnдо v_n +., найдем время

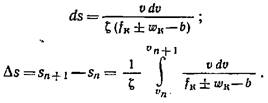
Для интегрирования уравнений (174) и (176) необходимо иметь характеристики удельных ускоряющих сил для режимов тяги, холостого хода и торможения с учетом профиля пути. Обычно зависимости силы тяги локомотива от скорости даны графически в виде кривых Fк ⁼ f(v), силы основного сопротивления движению подвижного состава W₀ — f₁(v), тормозные В_т = f₂(v) и др. рассчитываются в основном по эмпирическим формулам.

Графическое интегрирование уравнения движения поезда. Графические способы отличаются от аналитических тем, что значения скорости v, времени «дельта» t и пути «дельта» s не вычисляют, а определяют геометрическими построениями в виде отрезков в определенных масштабах. Все они основаны на приближенном интегрировании уравнения движения поезда.

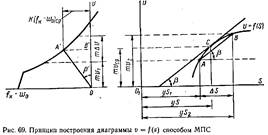
Графические способы широко применяются в практике тяговых расчетов «вручную», так как они обеспечивают наглядность и значительно ускоряют процесс решения тяговых задач, в особенности за счет применения специальных шаблонов.

4. Методика расчёта и построения диаграммы удельных сил, действующих на поезд. Анализ характера движения поезда.

Для большей наглядности и лучшего уяснения взаимосвязи равнодействующих сил и скорости движения удобно пользоваться диаграммой F_к— W₀ = f (v) или в виде удельных сил f_к — w₀ = «фи»(v), определяющей величину равнодействующей для любой скорости движения на прямом и горизонтальном пути. Так как сила сообщает поезду положительное или отрицательное

ускорение, то часто она называется ускоряющей силой, а диаграмма— диаграммой ускоряющих сил.

На рис показаны совмещенные диаграммы силы тяги F_Kи силы основного сопротивления W₀ в функции скорости v. Точка А пересечения линии силы тяги с линией силы основного сопротивления определяет скорость v_pравномерного движения данного поезда на прямом и горизонтальном пути

При скоростях, меньших~                                                                                    т. е. равнодействующая сила положительна, и поезд движется с ускорением, а при скоростях, большихт. е. равнодействующая сила отрицательна, и поезд движется с замедлением. Определив для разных скоростей величину F_K— W₀и разделив результат