

1Силы действующие на поезд
расчет можно вести в двух системах единиц кгс/кг=10Н/кг
![]() Н/кг
Н/кг
![]() кгс/кг
кгс/кг
![]() -
коэффициент учитывающий массу
-
коэффициент учитывающий массу
![]() =120
(км/ч2)/(кгс/т),
=120
(км/ч2)/(кгс/т),![]() =12(км/ч2)/(Н/т)
=12(км/ч2)/(Н/т)
режим тяги r = -fk-wk хол. ход r = -wk экстренное торможение r = -wk-bт
![]()
![]() уравнение
движения поезда
уравнение
движения поезда
3Методы интегрирования уравнения движ. поезда
Выделяют два способа аналитическое и графическое интегрирование. Аналитическое интегрирование уравнения движения поезда позволяет найти зависимость между скоростью v времени t и пройденного расстояния.
![]()
![]() проинтегрируем
проинтегрируем ![]()
![]() будем
рассматривать движение поезда в режиме тяги на прямом горизонтальном участке
пути. Что в приделах каждого интервала равнодействующая не меняется и остается
равной среднему значению на интервале.
будем
рассматривать движение поезда в режиме тяги на прямом горизонтальном участке
пути. Что в приделах каждого интервала равнодействующая не меняется и остается
равной среднему значению на интервале.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Графические способы решения уравнения движения поезда отличаются от аналитических тем, что значения скорости, времени и пути не вычисляют , а определяют геометрическим путем в виде отрезков в определенном масштабе , до начала применения вычислительной техники графический метод был основным.
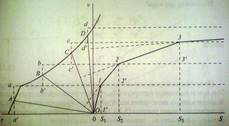
Большинство графических методов опираются на идею Дедуи, который предположил строить кривую скорости движения поезда пользуясь имеющейся зависимостью удельной равнодействующей сил от скорости движения. Идея Дедуи основана на том что тангенс углов образуемых касательной кривой V(t) с осью времени пропорц. ускоряющим усилиям.
Существует несколько способов интегрирования уравнения движения графическим способом. Одним из них является метод Липеца.
Численное интегрирование. Приемы нахождения приблизительного решения дифф. уравнения Крылов разделил на три группы 1) разложение общего интеграла в ряды 2)применения способа последовательного приближения 2) приближденное численное интегрирование.Достаточно найти частное решение удолитворяймое начальным условиям.
Метод Эйлера
![]()
4Тормозные задачи и методы их решения
По правилам для обеспечения безопасности движения поездов машинист должен иметь возможность при необходимости применив торможение скинуть скорость движения поезда вплоть до полной его остановки на определенном расстоянии, это расстояние называется тормозной путь Sт.
Длинной тормозного пути называется, расстояние проходимое поездом за время от момента поворота ручки крана машиниста до полной остановки.Sт=Sп+Sд От момента поворота крана машиниста в тормозное положение до момента прижатия тормозных колодок к колесом (дискам) проходит время называемое периодом подготовки тормозов tп в течении этого времени поезд проходит расстояние Sп, расстояние– путь подготовки тормозов с нажатыми колодками поезд проходит путь Sт называется действительным тормозной путь складывается из подготовки торм. к действию и действит. тормозному пути.
Решение тормозных задач сводиться к
нахождению одной из четырех величин по заданным трем Sт Vн Vк ![]()
Тормозные задачи делятся на 2 группы. К первой группе относятся задачи . которые в исходных данных содержат информацию о тормозных средствах поезда, ко второй группе относятся такие тормозные задачи для которых тормозной коэф. или силу необходимо определить.
Прмер пусть заданы Vн Vк ![]() ,
Sт–?
,
Sт–?
решение : Sт=Sп+Sд Sп =0,278 Vнtн Время подготовки торм. принимают приближенно в зависимости от длинны состава в осях до 200 осей 7 сек, от 200-300 10сек, а выше 300 12сек для грузовых. Выбираем нужное из трех
![]() до
200 осей
до
200 осей
![]() 200-300
200-300
![]() более
300
более
300
![]() –коэф.
трения
–коэф.
трения
Для графического решения задач в ТЛТ исполбзуют диаграмму удельных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.