Динамическое вписывание тепловоза. Радиус кривой для динамического вписывания. Наибольшая скорость движения локомотива в кривой

3. Динамическое вписывание тепловоза

Радиус кривой для динамического вписывания

Возвышение наружного рельса в кривой

Статическое давление колесной пары на рельсы

Определяем полюсное расстояние в положении наибольшего перекоса тележки

                                           (28)

где база тележки, ;

радиус кривой для динамического вписывания, ;

ширина колей зазора.

Наибольшая скорость движения локомотива в кривой определяем из условия комфортабельности по наибольшей величине непогашенного ускорения

                                       (29)

где непогашенное ускорение, .

Используя расчетную схему и вспомогательный график [1], определяем:

Составляем уравнения равновесия:

 

                                                       (30)

Определяем силы, входящие в уравнение равновесия:

Значение сил трения в опорных точках колес считаются равными для всех колесных пар тепловоза и они могут быть определены по формуле

                                                  (31)

где коэффициент трения между рельсами и бандажами, .

Определяем силу от возвышения наружного рельса по формуле

                                                 (32)

где часть веса тепловоза приходящееся на тележку, .

Определяем угол поворота тележки в положении ее наибольшего перекоса для передней тележки по формуле:

                                                 (33)

По графику [1] определяем суммарный момент .

Определяем суммарный момент. Задаваясь величиной отклонения кузова , определяем отклонения передних и задних опор передней тележки по формуле:

для передней опоры

                                               (34)

для задней опоры

                                               (35)

.

По графику [1] определяем возвращающие силы:

Находим возвращающий момент по формуле

                                             (36)

Значение , полученное из первого уравнения равновесия, подставляем во второе уравнение, после преобразований с учетом ранее найденных сил и моментов имеем систему уравнений

 

 

 

Приравнивая в уравнении  определим величину направляющего усилия и центробежную силу.

.

Определяем скорость при

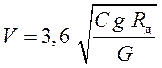                                                (37)

.

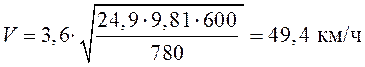Определяем центробежную силу приходящуюся на тележку по формуле

                                                (38)

Подставляя различные значения скорости решаем уравнения равновесия относительно  и , и полученные данные сводим в таблицу 5

Таблица 5

0	0,0	15,5	64,9	32,4	-0,1
5	0,3	15,3	65,0	32,5	0,0
15	2,3	14,1	65,8	33,3	0,8
20	4,1	13,0	66,4	33,9	1,4
30	9,2	9,8	68,4	35,9	3,4
40	16,4	5,3	71,1	38,6	6,1
50	25,6	-0,4	74,6	42,1	9,6
60	36,8	-7,4	78,9	46,4	13,9
70	50,1	-15,6	83,9	51,4	18,9
80	65,4	-25,1	89,7	57,2	24,7
90	82,8	-35,9	168,1	135,6	103,1
100	102,3	-48,0	96,3	63,8	31,3
110	123,7	-61,3	111,8	79,3	46,8
120	147,2	-75,9	120,7	88,2	55,7

Боковое давление колеса на рельс меньше направляющего усилия на величину силы трения в контакте колеса с внутренним рельсом т.е.

Рамное давление, т.е. усилие, передаваемое колесной парой на раму тележке, меньше направляющего усилия на величину сил трения обоих колес т.е.