






















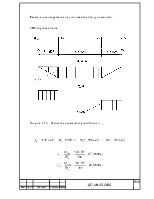






























Распределение вертикальной нагрузки между элементами верхней рамы
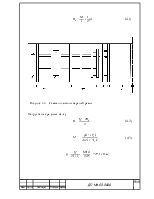
Для определения реакций в опорах используется уравнение 3-х моментов
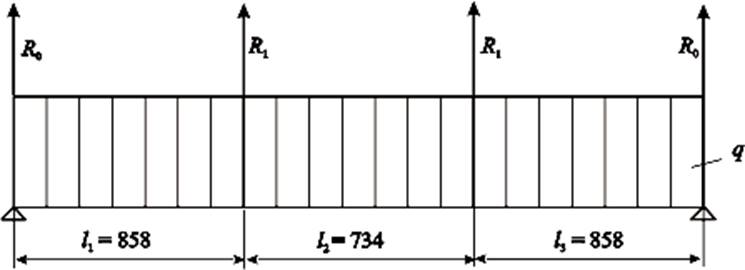
Рисунок 4.1 – Расчетная схема верхней рамы в поперечном сечении
Нагрузка на боковую балку
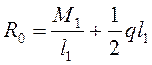 .
(4.1)
.
(4.1)
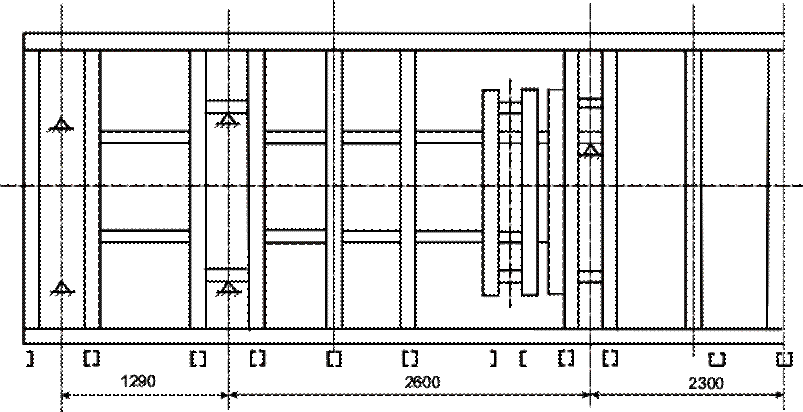
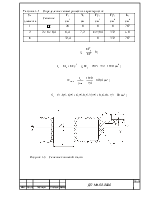
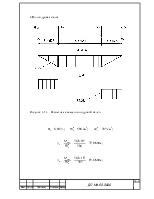
Рисунок 4.2 – Схема половины верхней рамы
Нагрузка на среднюю балку
![]() .
(4.2)
.
(4.2)
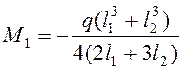 ;
(4.3)
;
(4.3)
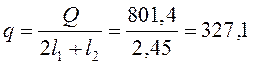 кН/м;
кН/м;
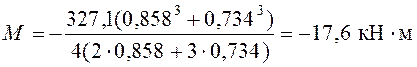 ;
;
Тогда по формулам (4.1-4.2) найдем нагрузку на боковую и среднюю балки
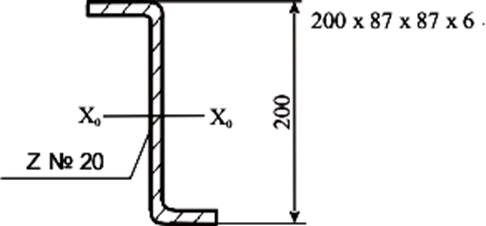
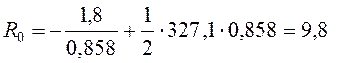 кН;
кН;
![]() .
.
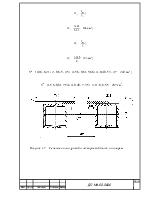
F = 21,11 см2; Iхо = 1259 см4
Рисунок 4.3 – Сечение боковой продольной балки
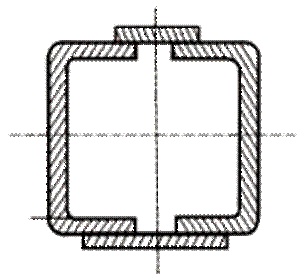
Рисунок 4.4 – Сечение центральной продольной балки
Таблица 4.1 – Определение геометрических характеристик
|
№ элемента |
Сечение |
F, см2 |
Y, см |
Fy, см3 |
Fy2, см4 |
I0, см4 |
|
1 |
|
26 |
0 |
0 |
0 |
707 |
|
2 |
2 ´ 8 ´ 0,4 |
6,4 |
7,2 |
|
332 |
» 0 |
|
Σ |
32,4 |
0 |
332 |
707 |
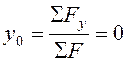 ;
;
![]() ;
;
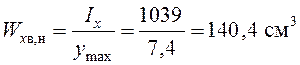 ;
;
![]() ;
;
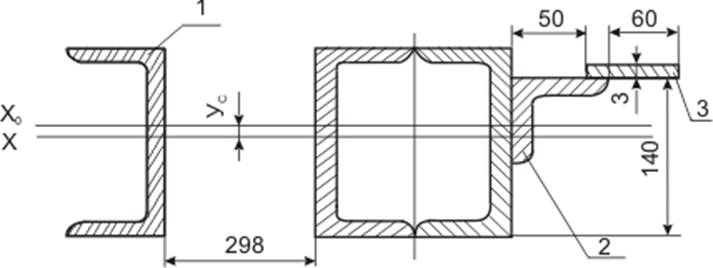
Рисунок 4.5 – Сечение концевой балки
Таблица 4.2 – Определение геометрических характеристик
|
№ п/п |
Сечение |
Кол. |
F, см2 |
Y, см |
Fy, см3 |
Fy2, см4 |
I0, см4 |
|
1 |
Швеллер № 18 |
3 |
62,1 |
0 |
0 |
0 |
3270 |
|
2 |
ë 75 ´ 75 ´ 6 |
1 |
8,78 |
2,94 |
25,81 |
75,88 |
46,6 |
|
3 |
0,3 ´ 8,5 |
1 |
2,55 |
5,15 |
13,13 |
67,61 |
» 0 |
|
å |
73,4 |
» 40 |
143,5 |
3317 |
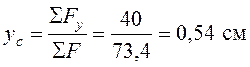 ;
;
![]() ;
;
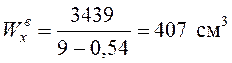 ;
;
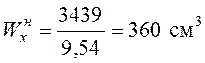 ;
;
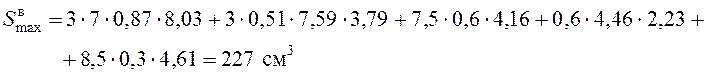 ;
;
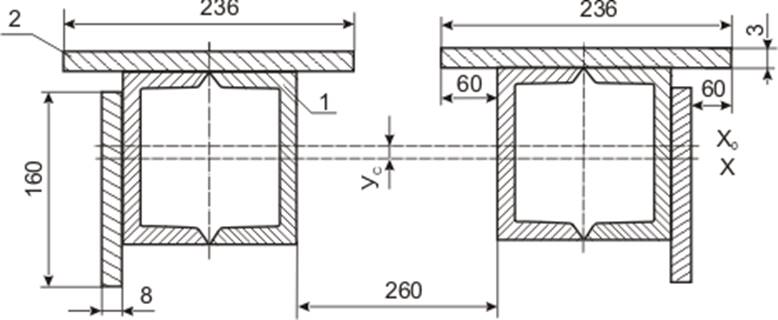
Рисунок 4.6 – Сечение шкворневой балки посередине и цилиндровой балки
|
№ п/п |
Сечение |
Кол. |
F, см2 |
Y, см |
Fy, см3 |
Fy2, см4 |
I0, см4 |
|
1 |
Швеллер № 14 |
4 |
62,4 |
0 |
0 |
0 |
1964 |
|
2 |
23,6 ´ 0,3 |
2 |
14,16 |
7,15 |
101,2 |
723,6 |
»0 |
|
3 |
0,8 ´ 16 |
2 |
25,6 |
-0,2 |
-5 |
1 |
546 |
|
å |
»102 |
»96 |
»725 |
2510 |
Таблица 4.3 – Определение геометрических характеристик
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
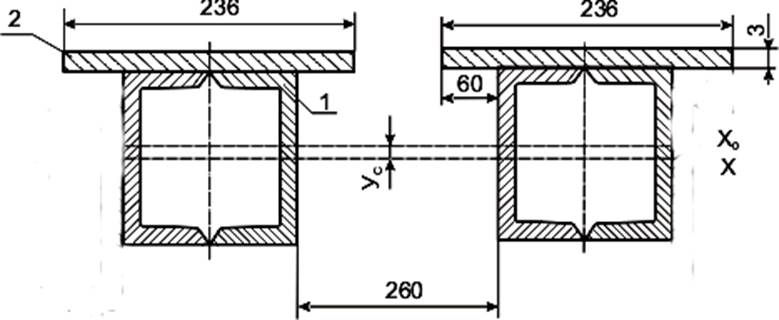
Рисунок 4.7 – Сечение цилиндровой и шкворневой балок по опорам
Таблица 4.4 – Определение геометрических характеристик
|
№ п/п |
Сечение |
Кол. |
F, см2 |
Y, см |
Fy, см3 |
Fy2, см4 |
I0, см4 |
|
1 |
Швеллер№14 |
4 |
62,4 |
0 |
0 |
0 |
1964 |
|
2 |
23,6 ´0,3 |
2 |
14,16 |
7,15 |
101,2 |
723,6 |
0 |
|
å |
76,6 |
»101 |
»724 |
1964 |
![]() ;
;
![]() ;
;
![]() ;
;
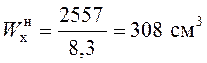 ;
;
![]() ;
;
![]() .
.
4.2 Расчёт центральной продольной балки
Центральная балка считается неразрезной, лежащей на 6-ти жестких опорах.
Равномерно распределенная по длине балки нагрузка равна
![]() ,
(4.4)
,
(4.4)
где R1 – нагрузка на среднюю продольную балку, кН;
l– длина балки, м.
![]()
Для расчета используется уравнение 3-х моментов.
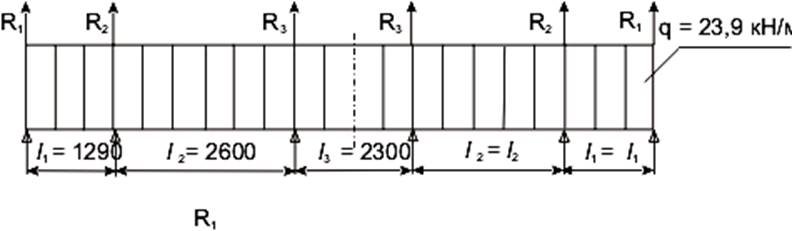
Рисунок 4.8 – Расчетная схема продольной центральной балки
Ввиду симметрии балки
![]()
![]()
![]()
![]() .
.
Пролеты 1 и 2
![]() ;
;
![]() ;
;
![]() .
(4.5)
.
(4.5)
Пролеты 2 и 3
![]() ;
;
![]() ;
;
![]() .
(4.6)
.
(4.6)
Решаем систему уравнений (4.5) и (4.6)
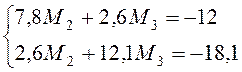 ;
;
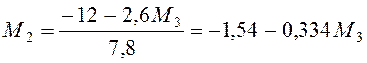 ;
;
2,6(-1,54 -0,334М3) + 12,1М3 = -18,1;
11,23М3 = -14,1;
М3 = -12,3 кН·м;
М2 = -1,54 -0,334(-1,25)=-11,0 кН·м;
М2 = -11,0 кН·м;
Определение опорных реакций
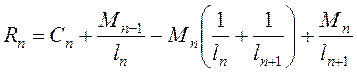 ;
;
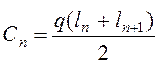 ;
;
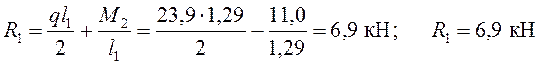 ;
;
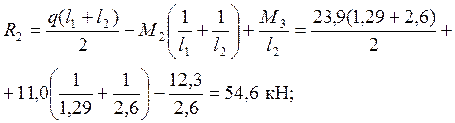
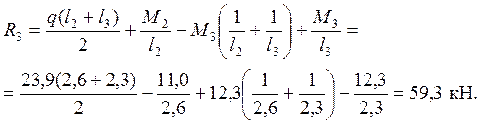
Проверка:
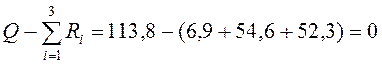 .
.
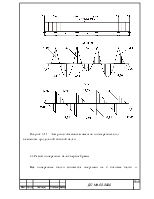
Построение эпюр изгибающих моментов и поперечных сил для продольной центральной балки
Пролет 1
Момент в пролете определяется по формуле
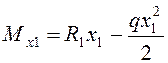 .
(4.7)
.
(4.7)
Максимальное значение момента будет в
точке, для которой ![]()
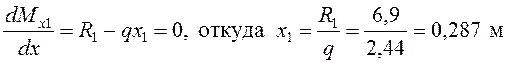 ;
;
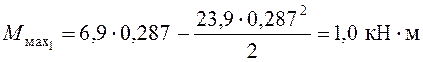 .
.
Момент над опорой 2
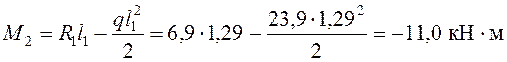 .
.
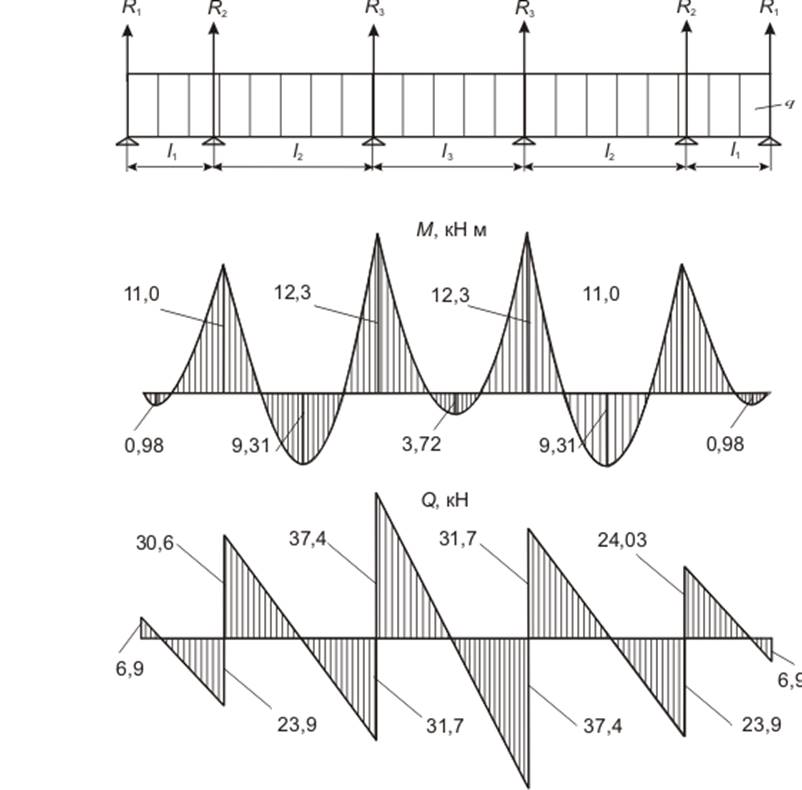
Рисунок 4.9 – Эпюры изгибающих моментов и поперечных сил в сечениях продольной центральной балки
Пролет 2
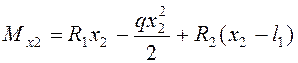 ;
;
![]() откуда
откуда
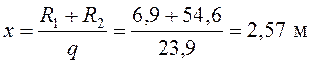 ;
;
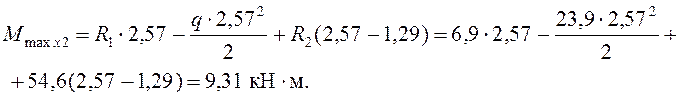
Момент над опорой 3
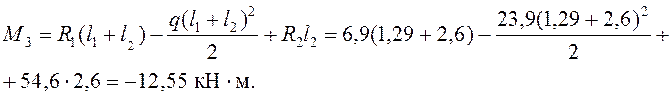
Пролет 3
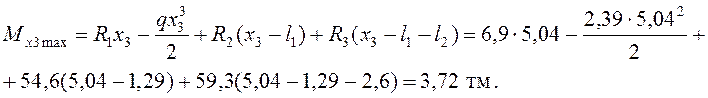
Определение напряжений в центральной продольной балке
Над опорой 2:
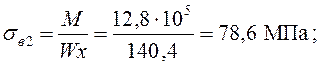
![]()
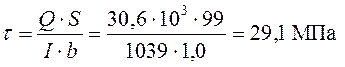 .
.
По энергетической теории прочности
![]() ;
;
Над опорой 3:
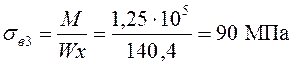 .
.
4.3 Расчёт боковой продольной балки
Расчётная схема боковой продольной балки аналогична расчётной схеме центральной продольной балки.
Нагрузка на боковую балку
R0 = 98 кН. Равномерно распределенная по длине балки
нагрузка 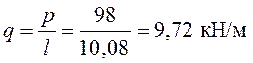 .
.
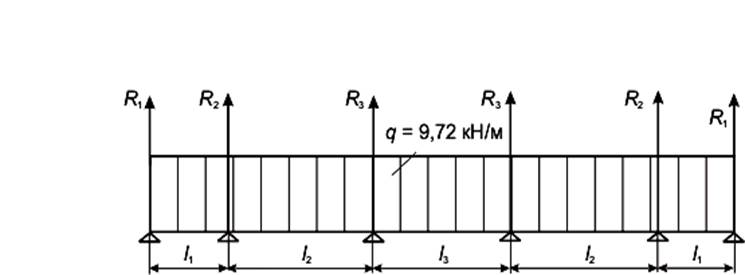
Рисунок 4.10 – Расчетная схема боковой продольной балки
Ввиду симметрии балки
![]()
![]()
![]() .
.
Расчёт балки производится при помощи теоремы 3-х моментов
![]() .
.
Пролёты 1 и 2
![]() ;
;
![]() ;
;
![]() . (4.8)
. (4.8)
Пролёты 2 и 3
![]() ;
;
![]() ;
;
![]() .
(4.9)
.
(4.9)
Решим систему уравнений (4.8) и (4.9)
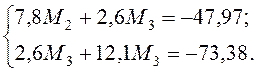
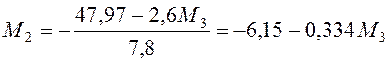 ;
;
![]() ;
;
11,23М3 = –57,9; М3 = –5,1 кН·м.
![]() кН·м;
кН·м;
М2 = –4,56 кН·м.
Определение опорных реакций
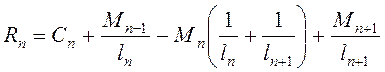 ;
;
![]() ;
;
![]()
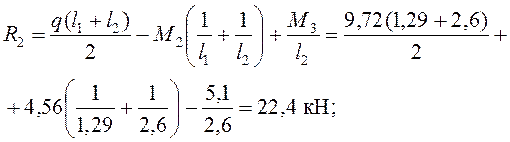
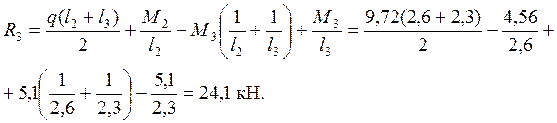
Проверка:
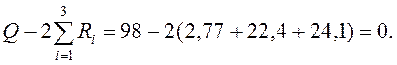
Построение эпюр изгибающих моментов и перерезывающих сил для боковой продольной балки
Экстремальные значения моментов в пролетах будут в тех же точках, что и на центральной балке.
Пролет 1
![]() ;
;
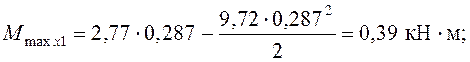
Момент над опорой 2
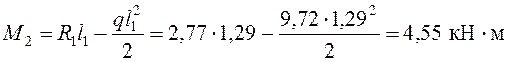 .
.
Пролет 2
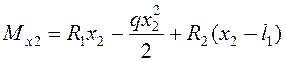 ;
;
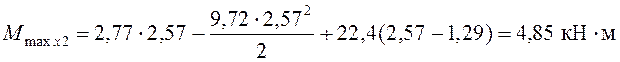 .
.
Момент над опорой 3
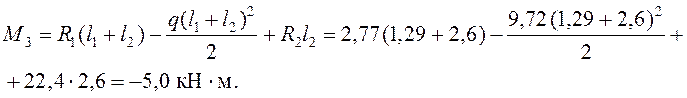
Пролет 3
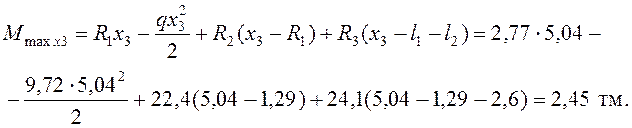
Определение напряжений в боковой продольной балке
Над опорой 2
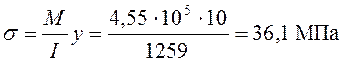 .
.
Посередине пролета 2
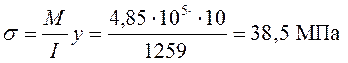 .
.
Над опорой 3
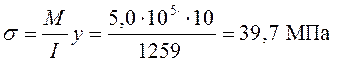 .
.
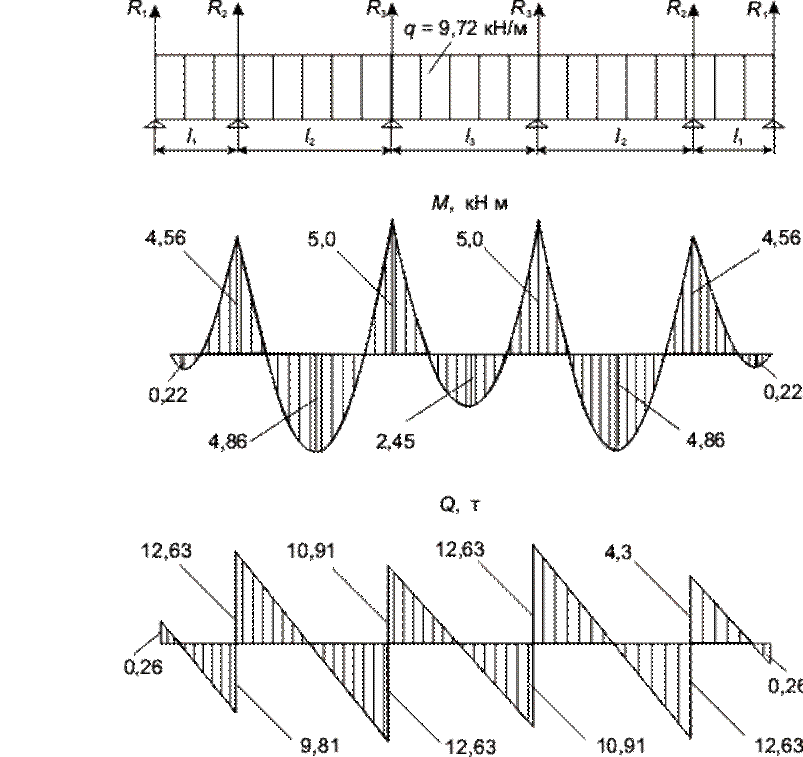
Рисунок 4.11 – Эпюры изгибающих моментов и поперечных сил в сечениях продольной боковой балки
4.4 Расчёт поперечных балок верхней рамы
Все поперечные балки считаются опертыми на 2 боковые балки и нагруженными от реакции 2-х средних продольных балок.
1 Концевая балка
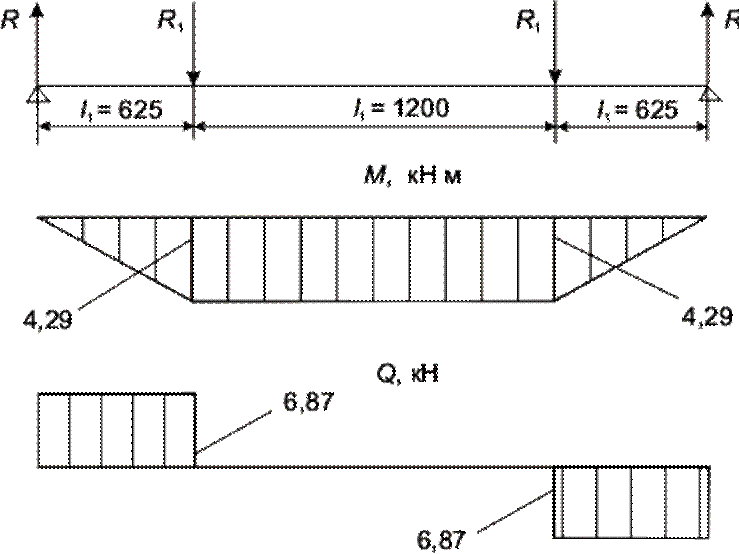
Рисунок 4.12 – Эпюры изгибающих моментов и поперечных сил для концевой балки
![]() ;
;
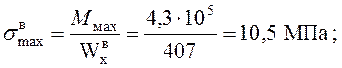
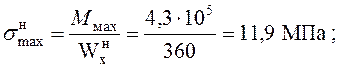
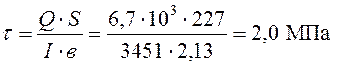 .
.
Касательные напряжения не учитываются ввиду их малости.
2 Шкворневая балка
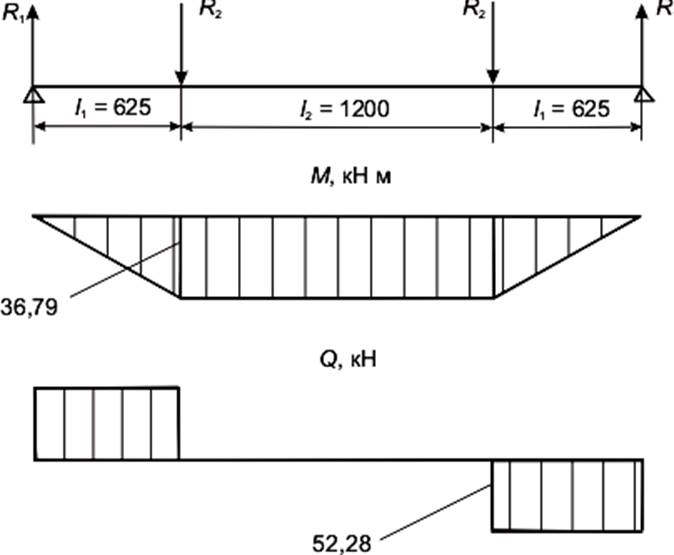
Рисунок 4.13 – Расчетная схема шкворневой балки
![]() ;
;
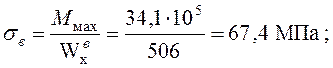
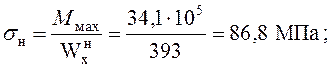
3 Цилиндровая балка
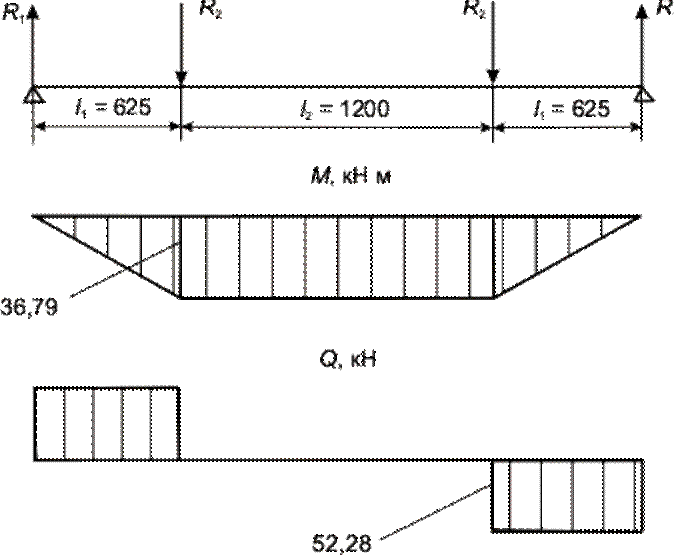
Рисунок 4.14 – Расчетная схема цилиндровой балки
![]() ;
;
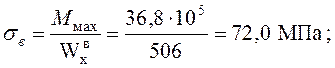
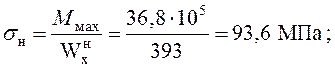
Вывод: Расчётные напряжения в элементах конструкции верхней рамы при статической нагрузке не превышают допускаемых
![]() .
.
4.5 Расчет лобовой стенки
Силы распора от насыпных грузов определяются в общем случае по формулам и схемам теорий статики и динамики сыпучих тел.
При расчете торцевых стенок по I режиму расчетное давление на единицу поверхности определяется по формуле
![]() ,
(4.10)
,
(4.10)
где 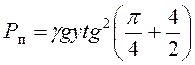 ;
;
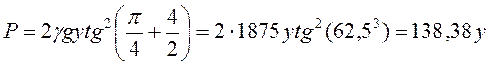 ; (4.11)
; (4.11)
теоретическая плотность перевозимого груза
![]()
φо – угол естественного откоса груза, φ = 35
у – расстояние от поверхности насыпного груза до точки, в которой определяется давление.
Для расчета воспользуемся схемой распределения нагрузки от распора между элементами лобовой стенки.
Для расчета стоек необходимо определить величину и характер изменения приходящихся на них распорной нагрузки, т. е. интенсивность
![]() .
.
Размеры лобовой стенки взяты по параметрам кузова внутри.
Для средней стойки интенсивность распорной нагрузки
![]() .
.
Изгибающий момент для стойки
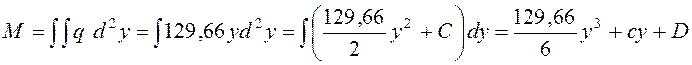 .
.
При у = 0 Q = 0.
![]() .
.
При у = 0 М = 0
![]() .
.
Следовательно
![]() .
.
Максимальный
изгибающий момент в заделке при ![]() м
равен
м
равен
![]() .
.
Для центральной стойки
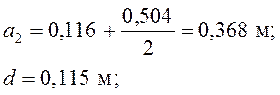
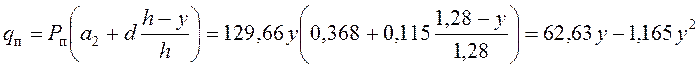 .
.
Изгибающий момент для стойки
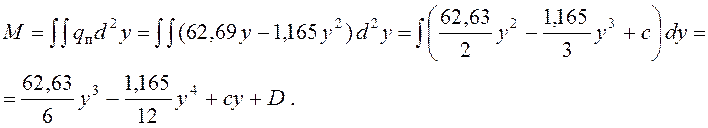
При у = 0 Q = 0
![]() .
.
При у = 0 М = 0
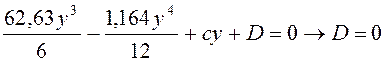 .
.
Следовательно
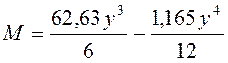 .
.
Максимальный момент в заделке при у = h = 1,28 м равен
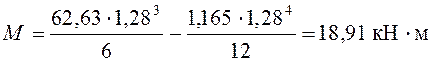 .
.
Таблица 4.5 – Геометрические характеристики сечения
|
№ п/п |
Сечение |
F, см2 |
Y, см |
Fy, см3 |
Fy2, см4 |
I0, см4 |
|
1 |
24,7 ´ 0,7 |
17,29 |
40,35 |
698 |
28150 |
1 |
|
2 |
40 ´ 0,8 |
32 |
20 |
640 |
12800 |
4267 |
|
3 |
5,3 ´ 0,8 |
4,24 |
0,4 |
1,7 |
0,7 |
– |
|
å |
53,53 |
1340 |
40951 |
4268 |
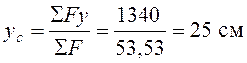 ;
;
![]() ;
;
![]() ;
;
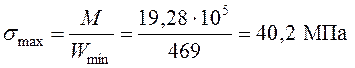 ;
;
![]() ;
;
![]() .
.
Сечение средней правой стойки в месте крепления к верхней раме
Таблица 4.6 – Геометрические характеристики сечения
|
№ п/п |
Сечение |
F, см2 |
Y, см |
Fy, см3 |
Fy2, см4 |
I0, см4 |
|
1 |
32 ´ 0,7 |
22,4 |
40,35 |
904 |
36470 |
1 |
|
2 |
11 ´ 0,8 |
8,8 |
34,5 |
304 |
10474 |
89 |
|
3 |
13 ´ 0,8 |
10,4 |
6,5 |
67,6 |
439 |
146 |
|
4 |
5,3 ´ 0,8 |
4,24 |
0,4 |
1,7 |
0,7 |
– |
|
å |
45,84 |
1277 |
47384 |
236 |
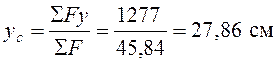 ;
;
![]() ;
;
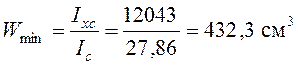 ;
;
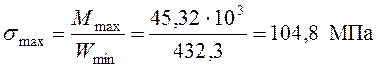 ;
;
[s] = 260 МПа;
smax < [s].
4.6 Расчет бopтa продольного. Разгрузка.
Продольный борт состоит из продольных и поперечных элементов, перекрытых листом. Решение такой системы представляет собой трудную задачу, поскольку она много раз статически неопределима. В целях упрощения считается, что такой борт работает как пластина. Расчетная схема представлена на рисунке 4.15.
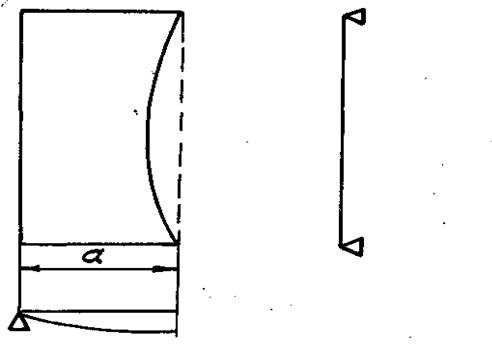
а=1260мм; в=10330мм; ![]()
Рисунок 4.15- Расчетная схема борта продольного
Для решения такой пластины воспользуемся следующими формулами:
![]()
![]() (4.12)
(4.12)
![]() (4.13)
(4.13)
![]()
![]() (4.14)
(4.14)
![]() (4.15)
(4.15)
![]()
![]()
![]() (4.16)
(4.16)
где b – длина свободной стороны пластины;
![]() W1 – стрела
прогиба в центре пластины;
W1 – стрела
прогиба в центре пластины;
![]() – стрела прогиба
посередине свободной кромки;
– стрела прогиба
посередине свободной кромки;
М1,М2 – изгибающие моменты в центре пластины;
![]() – изгибающий момент
посередине свободной кромки;
– изгибающий момент
посередине свободной кромки;
t – толщина пластины;
Р – интенсивность распределительной нагрузки.
Определяем интенсивность распределительной нагрузки:
![]() (4.17)
(4.17)
где Q- груз лежащий на борту;
![]() - вес борта,
- вес борта, ![]() =1,489т.
=1,489т.
![]() (4.18)
(4.18)
![]() т.
т.
Тогда
![]()
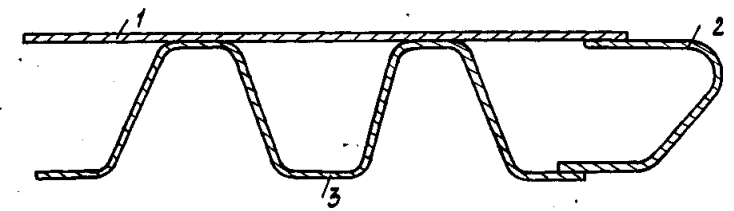
Определение приведенной толщины пластины:
![]() (4.19)
(4.19)
где Д- цилиндрическая жесткость пластины;
Ji- погонный момент инерции борта;
J- момент инерции борта;
![]() (4.20)
(4.20)
![]()
![]() - коэффициент Пуассона.
- коэффициент Пуассона.
![]() (4.21)
(4.21)
![]()
|
№ |
Сечение |
F |
Y |
Fy |
|
Jox |
|
1 |
0,7х110 |
77 |
0,35 |
26,95 |
9,43 |
3 |
|
2 |
24,06 |
8,62 |
207 |
1788 |
951 |
|
|
3 |
49 |
9,1 |
446 |
4058 |
1867 |
|
|
Σ |
150,06 |
680 |
5855 |
2821 |
![]()
![]()
Определение напряжений:
![]()
![]()
![]()
![]() (4.22)
(4.22)
По формуле 4.22
![]()
![]() (4.23)
(4.23)
Тогда
![]()
![]() (4.24)
(4.24)
![]()
Допускаемые напряжения для стали 09Г2
при разгрузке равны ![]()
![]()
Напряжение в расчетных сечениях меньше допускаемых, т.е. требуемая прочность обеспечена.
При оценке устойчивости вагона – самосвала при разгрузке принимаются следующие допущения:
– ось опрокидывания вагона находится в плоскости головок рельсов на расстоянии от оси пути, равном половине ширины колеи, т. е. 0,76 м (с внутренней стороны головки рельса). Плоскость головок рельсов принимается горизонтальной;
– кузов вагона находится в своем конечном положении под максимальным углом наклона a к нижней раме – 45о. Открытый продольный борт имеет перелом по отношению к плоскости пола кузова на конструктивный угол b = 9о;
– деформация пути и прогибы пружин рессорного подвешивания не учитываются;
– расчетная насыпная плотность груза определяется по техническому
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.