21) Пусть А1 и А2, В1 и В2, С1 и С2 – такие точки сторон ВС, СА, АВ треугольника АВС, что отрезки В1А2 и АВ, А1С2 и АС, С1В2 и СВ соответственно параллельны. Доказать, что треугольники А1В1С1 и А2В2С2 имеют равные площади.
22) Через вершину С меньшего основания ВС трапеции АВСD проведена прямая, параллельная стороне АВ и пересекающая диагональ ВD в точке Р. Доказать, что если DР=ВО (где О – точка пересечения диагоналей), то прямая, параллельная СD и проходящая через вершину В отсекает на второй диагонали отрезок АМ, равный ОС.
23) Точки А1, А2, А3 ,…, А12 расположены последовательно на линии параллелограмма А1А4А7А10 так, что его стороны разделены ими каждая на три равные части, а прямые А2А6 и А8А12, А3А11 и А5А9 отсекают внутри новый параллелограмм. Доказать, что его площадь составляет две девятых от площади исходного параллелограмма.
24) Площадь параллелограмма равна S. Прямые, проведенные через вершину и середины несмежных с ней сторон , отсекают от параллелограмма треугольник. Найти площадь оставшейся части параллелограмма.
25) Точки А1, А2, А3 ,…, А8 расположены последовательно на линии параллелограмма А1А3А5А7 так, что его стороны разделены ими каждая на две равные части, а прямые А2А5 и А6А1, А3А8 и А4А7 отсекают внутри новый параллелограмм. Доказать, что его площадь составляет одну пятую от площади исходного параллелограмма.
1) Чем отличается родство от параллельного проектирования?
2) Всегда ли найдется родство, отображающее заданный треугольник в равносторонний?
3) Является ли осевая симметрия родством?
4) Всякое ли аффинное преобразование плоскости является родством?
5) Что такое главные оси родства?
6) Может ли аффинное преобразование плоскости быть задано парой конгруэнтных треугольников?
7) Для любого ли аффинного преобразования существует обратное?
Будет ли оно тоже аффинным?
8) Может ли аффинное преобразование плоскости иметь аналитическое представление в виде системы:
а)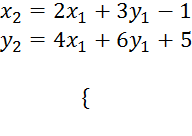 
? б) ?
9) Какие задачи в планиметрии называют «аффинными» ?
Как в их решении применяются аффинные преобразования ?
Мы рассматривали преобразования плоскости в порядке возрастания общности свойств: движение – это частный случай подобия, которое, в свою очередь, является разновидностью аффинного преобразования.
Изложение проводилось по сходной логической схеме, которая проявляется даже в следовании названий параграфов: после определений приводятся частные виды преобразований (употребляемые затем в разложениях общего вида), затем перечисляются наиболее существенные свойства и выводятся формулы аналитического представления преобразований. Это можно отобразить в таблице вопросов и ответов:
|
Вопросы |
Движения ( D ) |
Подобия ( Р ) |
Аффинные Преобразо-вания ( А ) |
|
1) Сохраняют ли - расстояния - углы - коллинеарность трех точек - простое отношение трех точек |
Да Да Да Да |
Нет Да Да Да |
Нет Нет Да Да |
|
2) Какой композицией всегда могут быть представлены ? |
либо |
||
|
3) Чем однозначно определяются ? |
Парой кон- груэнтных треуголь- ников |
Парой подобных треуголь- ников |
Парой произ вольных треуголь- ников |
|
4) Как задаются в декартовой системе координат ? |
Системой (6) стр.15 |
Системой (11) стр.41 |
Системой (19-20) стр.64 |
1. Аргунов Б.И. Преобразования плоскости. М.: Просвещение, 1976.
2. Атанасян Л.С., Базылев В.Т. Геометрия. Ч.1., гл.5. М.: Просвещение, 1986.
3. Ильина Н.И. Геометрические построения на плоскости: Учебно-методическое пособие.-Омск: Изд-во ОмГПУ, 1997.
4. Понарин Я.П., Скопец З.А. Перемещения и подобия плоскости: Пособие самообразования учителей.- К.: Радянська школа, 1981.
5. Четверухин Н.Ф. Проективная геометрия. М.: Просвещение, 1969.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.