

Методические указания по выполнению расчетно-графической работы
«РАСЧЕТ РАЗБИВОЧНЫХ ЭЛЕМЕНТОВ ДЛЯ ВЫНЕСЕНИЯ ПРОЕКТА В НАТУРУ»
на персональном компьютере
Требуется рассчитать разбивочные элементы для разбивки центров двух опор строящегося моста. Центр одной опоры должен быть вынесен методом прямой угловой засечки, центр другой опоры – методом полярной засечки. Для контроля последующих разбивочных работ предусмотреть избыточные измерения – прямую засечку с трех пунктов, полярную – с двух.
Для получения задания на работу запустите файл “dTask.mcd”. Откроется окно системы «Mathcad», содержащее заголовок, схему разбивочной сети, задание, список исходных данных и план текста отчета.
Впишите в заголовок ваши фамилию, номер группы и указанный преподавателем индивидуальный номер варианта, присвоив его значение переменной “var”. При этом произойдет автоматическая настройка задания на ваш вариант.
На схеме сети показано расположение геодезических пунктов, начала и конца мостового перехода, опор моста. Пронумерованы все разбивочные углы - относящиеся и не относящиеся к Вашему заданию.
В задании определено, для каких разбивочных работ надо выполнить расчеты.
В пункте 1 задания указаны:
- номер опоры, центр которой должен быть вынесен методом прямой угловой засечки;
- имена трех пунктов, с которых должны быть выполнены засечки;
- номера разбивочных углов, которые надо вычислить.
В пункте 2 задания указаны:
- номер опоры, центр которой должен быть вынесен методом полярной засечки;
- имена двух пунктов, с которых будут выполняться полярные засечки;
- номера разбивочных углов для полярных засечек.
Список исходных данных включает координаты х, у геодезических пунктов A, B, C, D и точки Н - начала мостового перехода (хН=1000 м, уН=1000 м), а также расстояния d между точками на оси моста.
Координатные оси направлены: ось х – из точки Н по оси мостового перехода, ось у – перпендикулярно вправо. Поэтому ординаты у центров всех опор равны уН. Абсциссы х центров опор следует вычислить, используя заданные расстояния d между точками по оси перехода. Например, x2=xН+d1+d2.
Для выполнения задания необходимо провести следующую работу.
1. Вычислите разбивочные углы b для выноса центра опоры методом прямой угловой засечки. Номер опоры и имена трех пунктов, с которых должна быть выполнена засечка, а также номера разбивочных углов, которые надо вычислить, указаны в пункте 1 задания.
Каждый разбивочный угол b вычисляется как разность двух дирекционных углов. Например, угол для засечки опоры 2 с пункта D (см. схему) определится по формуле b15=aDC-aD2.
Дирекционные углы линий, образующих угол b, вычисляют по координатам концов линий. Например,
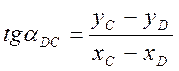 .
.
При этом надо верно сообразить четверть дирекционного угла.
Вместо вычислений по последней формуле можно использовать встроенную функцию angle системы «Mathcad», применяемую в следующем формате
aDC := angle(xC - xD, yC - yD).
Возвращаемый функцией угол выражен в радианах. Для перехода от радианов к градусам, минутам и секундам воспользуйтесь встроенной в задание функцией rgms в следующем формате rgms(aDC) =.
Выполните контрольные вычисления.
Используя два вычисленных разбивочных угла и дирекционные углы линий АВ или CD , вновь определите дирекционные углы линий засечки. Например,
aD2 = aDС - b15 и aC2 = aСD - b10.
Затем вычислите координаты центра опоры по формулам
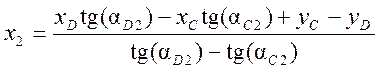 ,
,
![]() или
или ![]() .
.
Полученные координаты центра опоры (в данном случае х2, у2) должны совпадать с вычисленными ранее.
Для проверки правильности третьего разбивочного угла повторите контрольные вычисления для другой комбинации разбивочных углов.
2. Вычислите разбивочные углы b и расстояния в d для выноса второго центра опоры методом полярной засечки от двух пунктов. Номер опоры и имена обоих пунктов, опираясь на которые должны быть выполнены засечки, а также номера соответствующих разбивочных углов указаны в пункте 1 задания.
Разбивочные углы b вычисляется так же, как в пункте 1.
Расстояние от пункта геодезической сети (например, D) до центра опоры (например, 2) вычисляется по формуле
![]() .
.
Выполните контрольные вычисления. Так же, как в пункте 1 вычислите дирекционный угол для линии засечки (в нашем примере - aD2) и воспользуйтесь формулами прямой геодезической задачи
x2 = xD + dD2 cos aD2,
y2 = yD + dD2 sin aD2.
Такие же вычисления выполните и для полярной засечки со второго указанного в задании пункта.
3. Составьте список вычисленных разбивочных элементов и вычертите разбивочный чертеж в избранном вами масштабе. На разбивочном чертеже должны быть показаны те пункты и вычисленные элементы, которые использованы в выполнении вашего задания.
Разбивочный чертеж может быть исполнен средствами известного вам графического редактора или вручную.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.