Расчет переходных процессов в линейных электрических цепях. Определение принужденных составляющих

Балтийский   Государственный  Технический  Университет

им. Д.Ф.Устинова «Военмех»

Кафедра  электротехники

Курсовой  проект  по электротехнике

Тема  проекта: «Расчет  переходных  процессов  в  линейных  электрических   цепях»

Студент:      

Группа: Н-522

Преподаватель:

Оценка:

Подпись:

Санкт-Петербург

2004 г.

Оглавление

1.Составление характеристического уравнения путем  использования выражения для входного сопротивления цепи на переменном токе …………………………………1

2.Определение принужденных составляющих….……….2

3.Определение начальных условий……………….……....3

4.Составление дифференциальных уравнений по законам Кирхгофа……………………………………………………4

5.Составление дифференциальных уравнений методом

D-алгебраизации…………………………………………...5

6.Анализ полученных дифференциальных уравнений….7

7.Решение дифференциальных уравнений классическим методом……………………………………………………..8                                                                   

8.Определение остальных токов и напряжений………...10

9.Операторный метод расчета переходного процесса….12

10.Расчет токов i₁,i₂,i₃ методом узловых потенциалов…14

11.Расчет токов i₁,i₂,i₃ методом эквивалентного генератора…………………………………………………16

12. Расчет токов i₁,i₂,i₃ методом контурных токов……...18

13.Расчет переходного процесса методом пространства состояний………………………………………………….20

14.Решение системы дифференциальных уравнений, составленной в форме Коши…………….……………….22

15.Сводная таблица проверок……………………………25

16.Графики токов и напряжений, рассчитанных классическим методом…………………………………...27

Входные данные к курсовому проекту

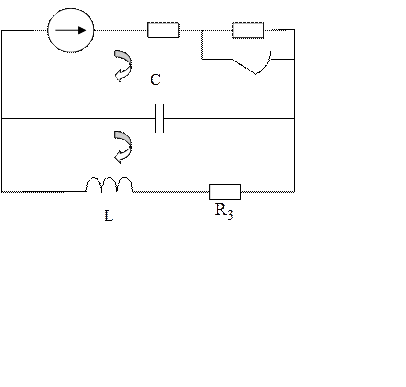
1.Схема цепи:

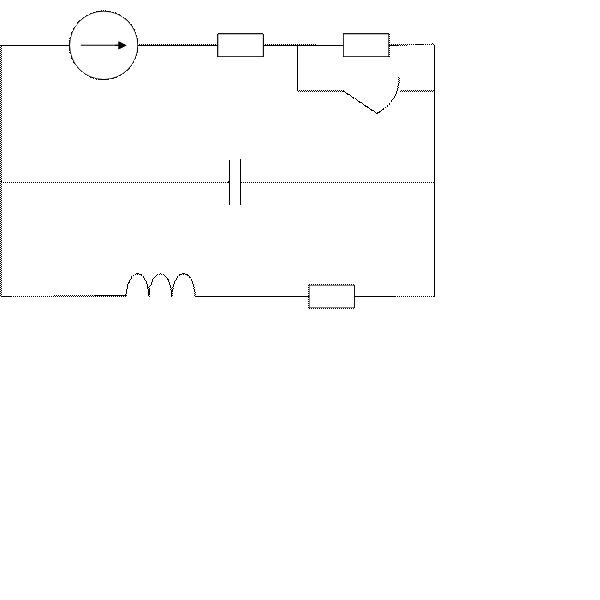
2.Номиналы элементов цепи:

E=250B;

C=0.6*10^-6Ф;

L=0.01Гн;

R₁=600 Ом;

R₂=300 Ом;

R₃=300 Ом;

3.Коммутация: замыкание ключа.

1.Составление характеристического уравнения путем  использования выражения для входного сопротивления цепи на переменном токе

Так как исходная цепь не содержит магнитосвязанных ветвей, то для составления характеристического уравнения цепи достаточно найти выражение входного сопротивления двухполюсника на переменном токе, заменить в полученном выражении jw на b и приравнять полученное выражение нулю. Уравнение Z_вх(jw) = 0 совпадает с характеристическим.

Пусть  Z₁=R₁,

Z₂=R₂,

      

Z₃=            ,                       

Z₄=R₃,   

Z₅= jwL;

Тогда

 

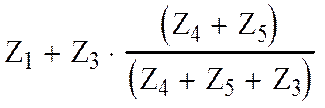Z_вх(jw) =                                          =

 

=

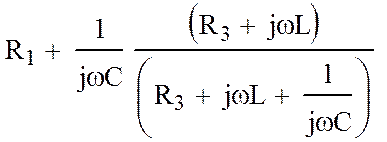(1).     

Заменим в выражении (1) jw на b:

 

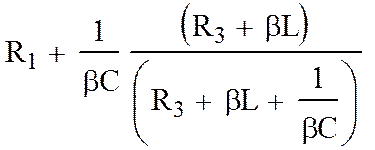Z_вх(b) =                                                =

 

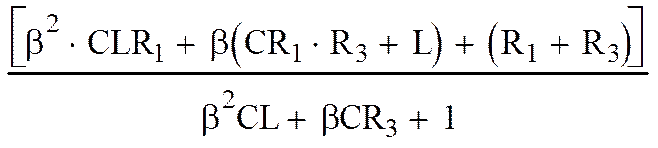=                                                                                   (2).

Характеристическим уравнением исходной цепи является числитель выражения (2).

Найдем корни характеристического уравнения:

 

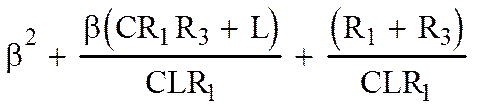= 0 (3).

 

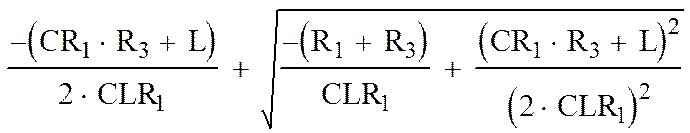b₁=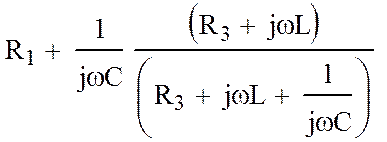                                                                                  

,

 

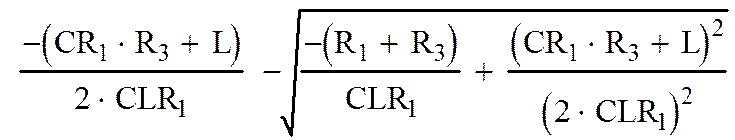b₂=                                                                                  ,

(4),(5).                                                                                

Подставляя в выражения (4) и (5) численные значения номиналов элементов, получим корни характеристического полинома:

b₁= -12076,6 с^-1;

b₂= -20701,2 с^-1;

 

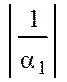t₁=        =8,28*10^-5 c;

t_п.п.= 3t₁= 2,48*10^-4 c;  (6).

Определим принужденные составляющие.

Рассмотрим цепь через очень большой промежуток времени после коммутации и найдем токи в ветвях цепи, а также значения падений напряжения на отдельных элементах:

 

 

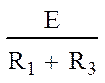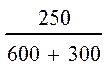=                 =                 = 0,278 A;   (7)     

 

= 0 A; (8)                             

 

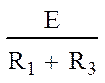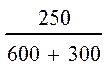=     =              =                =0,278 A; (9)

 

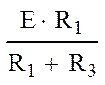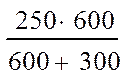=                =                   = 166,8 В;  (10)

                                                     

= 0 В; (11)

 

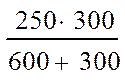=                   = 83.40 В;  (12) 

                                                

= 0 В;  (13)             =      =83,40 В.  (14)         

Определение начальных условий

Для определения начальных условий воспользуемся законами коммутации:

U_c(0_-)= U_c(0), I_l(0_-)= I_l(0) 

 

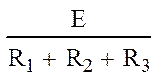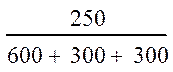(0)=    (0)=                      =                        = 0,208 A;             (15)

 

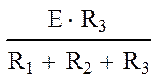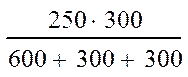(0) =      (0)*R₃=                    =                          = 62,50 B;

(16)

Составление дифференциальных уравнений относительно                                             

и       с помощью законов Кирхгофа

Для исходной цепи второго  порядка, содержащей два узла и три ветви, необходимо составить три уравнения, записанных по законам Кирхгофа, и одно уравнение связи вида I_c= C