Начертить график зависимости напряжённости от расстояния до центра шара
Поле равномерно заряженного шара.
Пусть заряд q равномерно распределен по шару радиусом а. Поле такой системы, очевидно, также центрально-симметричное, поэтому и здесь для нахождения поля следует в качестве замкнутой поверхности взять концентрическую сферу. Сфера радиусом
r < а охватывает заряд 
ибо
в нашем случае заряды относятся как объемы, а последние как кубы радиусов.
Поэтому согласно теореме Гаусса
Откуда
;
0<r<=R
Ф=E 4 π r^2=(1/ЭПСИЛОН0) ρ 4/3 π (R^3); E=ρ*r/3 ЭПСИЛОН0
т. е. внутри равномерно заряженного шара напряженность растет линейно с расстоянием r от его центра.
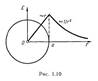
За пределами 
q=ρ 4/3
π R^3
7. Применение теоремы Гаусса для вычисления напряженности поля равномерно заряженной нити. Начертить силовые линии равномерно заряженной нити.
Силовые линии радиальные в плоскости, перпендекул. нити.
Поток ч/з замкнутую пов-ть S будет определяться только боковой поверхностью цилиндра
Ф=Е*2*pi*r*h=(1/ξ0)*λ*h
λ –линейная плотность заряда
8. Электрический диполь:дать определение Эл.диполяи дипольного момента.Получить выражения для потенциала и напряженности поля диполя. Начертить силовые линии поля диполя.
Электрический диполь — это система из двух одинаковых по модулю разноименных точечных зарядов + q и — q. находящихся на некотором расстоянии l друг от друга. Если расстояние между зарядами оч.мало, то диполь называется элементарным.
- дипольный
момент
Выберем произвольную точку в пр-ве, расстояние между диполями и точкой=r
распределение во всем пространстве
- потенциал диполя
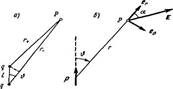
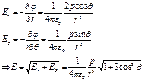
- распределение напряженности поля диполя
9. Электрический диполь:дать определение Эл.диполяи дипольного момента.
Поведение во внешнем электрическом поле:момент сил, действующих на диполь во внешнем поле, потенциальная энергия диполя во внешенем поле, сила, действующая на диполь во внешнем поле.
Электрический диполь — это система из двух одинаковых по модулю
разноименных точечных зарядов + q и — q. находящихся на некотором
расстоянии l друг от друга. Если расстояние между зарядами оч.мало, то диполь
называется элементарным.
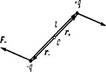- момент сил действующих на диполь.
М=qElsinα=PEsinα
, М=0 при
α =0 или α=π
Потенциальная энергия
диполя во внешнем поле
W=-Elcosα=-[p,E]
Сила, действующая на диполь в неоднородном поле
F=-gradW Пусть поле неоднородно в направлении х, тогда Fx=p(dE/dx)cosα cosα-очень мал,Сила действует в направлении более сильного поля.
10.Свойства электростатического поля в проводниках. Получить значения напряж.электростат.поля у пов-ти заряж.проводника.Проводники во внешнем электростатич.поле.
1) напряж.поля внутри проводника=0
2)напрях.поля вблизи прводн.направл.перпендекул.пов-ти
3)весь проводник явл-ся эквипотенциальным объемом
4)Если проводнику сообщ.заряд, то он распред-ся по пов-ти проводника
5)Поведение полых и сплошных проводников одинаково при сообщ.ему Эл.заряда
6)У поверхности проводника:Ф=ЕdS=
;
Напряженность поля вблизи пов-ти создано всеми зарядами в пров-ке.
Проводники во внешнем электростатич.поле.
На проводн. Во внешн.электростатич.поле возник.индуцирован.заряды. Двиг-ся электроны против линий поля, проводники разрывают силов.линии. вычислить индуц.заряд на пров-ке сложно.
Метод зеркальных отражений-принимается к вычислению инд.заряда на б\к большой заземленной проводящей плос-ти. Потенциал пл-ти обрашается в 0.
2заряда + и - .если над плос-тью есть точечный з-д q, и поле, ькоторое созд-ся элем-ным зарядом, и отрицат.заряды индуцированы, то это подобно системе 2х точечных зарядов.
11.электроемкость проводников. Электроемкость уединенной сферы.
Понятие электроемкость: чем больше заряд, чем болешей потенциал он будет приобретать
[Ф]- Электроемкость
проводника-это св-во проводника, определяется размерами, формами и
свойствами окруж.среды.
Электроемкость уединенной сферы
Дан заряд q, радиус сферы R, надо вычислить
-электроемкость уединенной сферы определяется только
радиусом.
12.Конденсаторы, электроемкость конденсаторов. Соединения конденсаторов. Вычисление электроемкости плоского конденсатора.
Конденсаторы-устройства, позволяющие накапливать заряд. Конд.вып-ся в виде 2 проводников располож.близко друг к другу-обкладки. Конденсаторы бывают плоские, сферические и цилиндрические.
Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга.
- электроемкость
конденсатора.
Электроемкость опр-ся формой контура, размерами и средой, не зависит от заряда.
Для плоского конденсатора
Заряды на внутр.обкладке б\к большие, d очень мало по сравнен.с обкладками.напряж.внутри конденсат-принцип суперпозиции, вне конденсатора поле отсутствует.Внутри
- вывод электроемкости плоского конденсатора, не
зависит от заряда
13.Конденсаторы.Электроемкость конденсаторов. Вычисление электроемкости сферического конденсатора.
Конденсаторы-устройства, позволяющие накапливать заряд. Конд.вып-ся в виде 2 проводников располож.близко друг к другу-обкладки. Конденсаторы бывают плоские, сферические и цилиндрические.
Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга.
- электроемкость
конденсатора.
Электроемкость опр-ся формой контура, размерами и средой, не зависит от заряда.
Электроемкость сферического конденсатора, обкладки-2 концентрические сферы, внутри поле электростатическое, снаружи нет
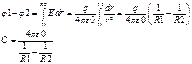- вывод электроемкости
сферического конденсатора, где R1 и R2– радиусы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.