Аппроксимация функции по методу наименьших квадратов. Коэффициенты системы нормальных уравнений линейной модели

Лабораторная работа № 4

Аппроксимация функции по методу наименьших квадратов.

Очень часто при анализе эмпирических данных необходимо найти явную функциональную зависимость между двумя величинами  и , полученными в результате измерений. Поскольку опытные данные всегда содержат ошибки, то строить интерполяционный многочлен  не оптимально, так как при интерполяции ошибки повторяются. Желательно по возможности сгладить и минимизировать ошибки наблюдений. Этот результат достигается построением многочлена наилучшего  среднеквадратического приближения по методу наименьших квадратов.

Итак, если  аппроксимируется многочленом вида , то есть система базисных функций имеет вид , то неизвестные коэффициенты многочлена  по методу наименьших квадратов определяются из решения системы (4.1.7).

В § 4.1 курса лекций описан пример «ручного» вычисления коэффициентов линейной и квадратичной модели по методу наименьших квадратов. Решим аналогичную задачу средствами Mathcad различными способами. Сформируем вначале векторы исходных данных

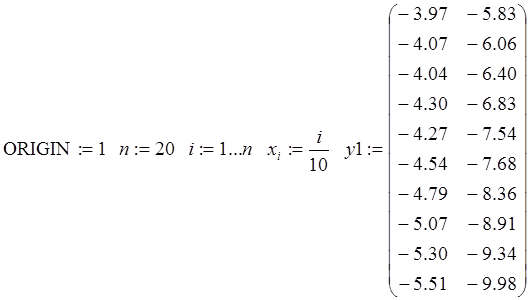
В алгебре матриц в среде Mathcad доступны несколько очень удобных встроенных функций. Например,

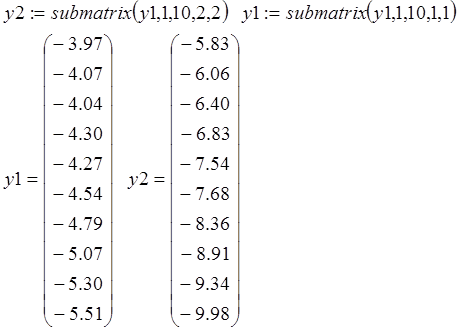
Функция  извлекает из матрицы  подматрицу, содержащуюся в  со строки  по строку  и со столбца с номером  по номер .

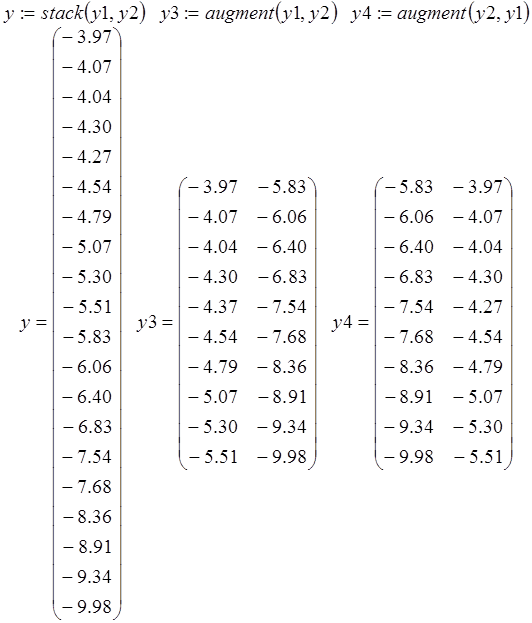
Функции  наоборот формируют одну матрицу из двух. После работы  получается массив, сформированный расположением  над , при этом матрицы  и  должны иметь одинаковое число столбцов. Функция  располагает матрицы  и  рядом,  справа от ; эти матрицы должны иметь одинаковое число строк.

Функции  возвращают число столбцов и строк матрицы ,  соответственно наименьшее и наибольшее значение элементов в ,  - число элементов в векторе ,  - индекс последнего элемента в векторе  с учетом значения переменной .

Построим линейную и квадратичную модель по формулам (4.1.8) и (4.1.9). Для этого вычислим следующие величины. Перед их вычислением введем еще одну предопределенную переменную пакета Mathcad . Эта величина определяет допустимую погрешность для различных