








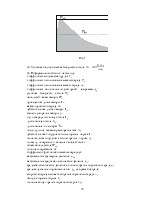

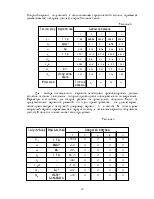



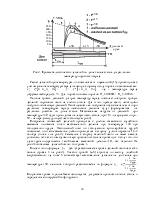
Решения обратной и прямой задач внутренней баллистики
1. Обратная задача внутренней баллистики
Решение ОЗВБ ставит своей целью поиск
оптимального сочетания конструктивных размеров канала ствола (свободного
начального объема ![]() , приведенной
, приведенной ![]() и фактической длины каморы
и фактической длины каморы ![]() , степени уширения каморы
, степени уширения каморы ![]() , длины пути снаряда по каналу
ствола
, длины пути снаряда по каналу
ствола ![]() , длины канала ствола в
калибрах
, длины канала ствола в
калибрах ![]() ) и условий заряжания
(плотности заряжания
) и условий заряжания
(плотности заряжания ![]() , относительной массы
снаряда
, относительной массы
снаряда ![]() , относительного импульса
давления газов
, относительного импульса
давления газов ![]() ).
).
Формулировка ОЗВБ, данная выше, является обобщенной и ей отвечает бесчисленное множество решений. Задача проектировщика - быстро найти среди этого множества решений оптимальное. Для поиска оптимального решения требуется проведение большого количества расчетов в итерационном цикле. Задача решается по периодам явления выстрела на основе аналитического метода профессора Н.Ф. Дроздова.
Предварительный (пиростатический) период.
Этот период начинается с момента воспламенения
заряда и заканчивается в момент достижения давления в канале ствола, равного
давлению форсирования ![]() . Давление
воспламенителя равно .
. Давление
воспламенителя равно . 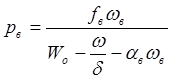 (1)
(1)
Если давление воспламенителя задано, то из (1) легко найти массу воспламенителя:
. 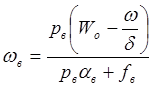 (2)
(2)
Основное уравнение пиростатики с учетом давления воспламенителя имеет вид
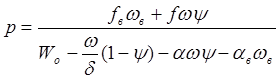 (3)
(3)
или
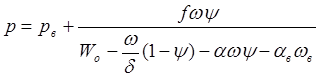 (4)
(4)
Уравнение (4) позволяет найти долю заряда, сгоревшего в
предварительном периоде ![]() , если
положить p=
, если
положить p=![]() :
:
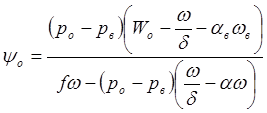 (5)
(5)
Вводя плотность заряжания ![]() и
вынося в знаменателе за скобки
и
вынося в знаменателе за скобки ![]() , после
несложных алгебраических преобразований получаем
, после
несложных алгебраических преобразований получаем
. 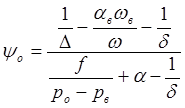 (6)
(6)
Если пренебречь влиянием массы воспламенителя по сравнению с массой заряда, то уравнение (6) можно записать как
. 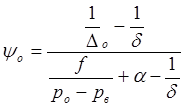 (7)
(7)
Теперь, зная ![]() с помощью
уравнения
с помощью
уравнения
![]() (8)
(8)
найти относительную толщину пороха, сгоревшую к началу движения снаряда. Уравнение (8) может быть решено численно, либо методом Кордана, а в случае двухчленного представления
![]() (9)
(9)
аналитически:
. 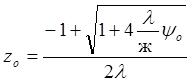 (10)
(10)
Подкоренное выражение в (10) можно преобразовать, если воспользоваться уравнением поверхности горения порохового зерна, которое в случае двучленного представления имеет вид
. ![]() (11)
(11)
Сравнивая (10) и (11), находим
. ![]() (12)
(12)
Зная параметры ![]() ,
, ![]() и
и ![]() можно
записать
можно
записать
![]()
Тогда приведенная длина свободного объема каморы в момент начала движения снаряда
. ![]() (13)
(13)
Время предварительного периода может быть рассчитано из основного уравнения пиростатики в дифференциальной форме:
. ![]() (14)
(14)
Правая часть (14) из-за сложного
характера изменения параметров ![]() и
и ![]() в аналитическом виде не может
быть найдена. Для аналитического решения необходимо ввести некоторые допущения.
Положим, что
в аналитическом виде не может
быть найдена. Для аналитического решения необходимо ввести некоторые допущения.
Положим, что ![]() , где
, где ![]() объем при
объем при ![]() будет равен (влиянием объема
газов воспламенителя пренебрегается):
будет равен (влиянием объема
газов воспламенителя пренебрегается):
. ![]() (15)
(15)
Тогда уравнение (14) запишется 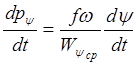 .
(16)
.
(16)
Для расчета скорости газообразования ![]() можно воспользоваться уравнением
можно воспользоваться уравнением
![]() . Учитывая, что
. Учитывая, что ![]() , найдем
, найдем
![]() (17)
(17)
Для трубчатого или ленточного пороха поверхность при
горении изменяется мало, поэтому в (17) можно положить ![]() , тогда
, тогда
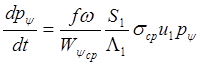 (18)
(18)
Обозначив
, 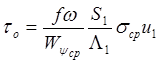 (19)
(19)
находим
. ![]() (20)
(20)
Интегрирование (20) дает 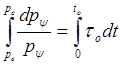 .
Отсюда находим
.
Отсюда находим
![]() (21)
(21)
Поскольку и известные величины, то из (21) находим время предварительного периода
. ![]() (22)
(22)
Пиродинамический период.
Пиродинамический
период - это период, когда относительная степень ![]() газификации
изменяется от
газификации
изменяется от ![]() до 1.
до 1.
Для расчета пиродинамического периода воспользуемся упрощенной системой дифференциальных уравнений внутренней баллистики:
1. Закон скорости горения
. ![]() (23)
(23)
2. Уравнение движения снаряда
. ![]() (24)
(24)
3. Закон газообразования
. ![]() (25)
(25)
4. Основное уравнение пиродинамики:
. ![]() (26)
(26)
Задача заключается в нахождении зависимостей,
связывающих четыре переменные величины: ![]() ,
v,и p.
,
v,и p.
Найдем скорость снаряда v. Для этого преобразуем уравнение движения снаряда
(24) следующим образом ![]() . Откуда
. Откуда
. 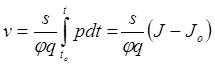 (27)
(27)
Умножим и разделим правую часть (27) на импульс горения
пороха ![]() :
:
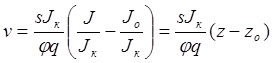 .
.
Обозначив ![]() будем иметь
уравнение
будем иметь
уравнение ![]() . (28)
. (28)
Для конца горения пороха (28) принимает вид
![]() (29)
(29)
Найдем путь снаряда ![]() .
Для этого воспользуемся уравнением (26), записав его следующим образом,
учитывая, что
.
Для этого воспользуемся уравнением (26), записав его следующим образом,
учитывая, что
![]() (30)
(30)
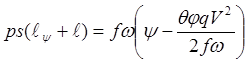
Обозначив предельную скорость снаряда при заданных условиях заряжания как
![]() , (31)
, (31)
находим 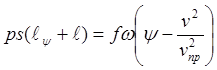 . (32)
. (32)
С другой стороны, уравнение движения снаряда (24) может быть представлено в виде
![]() , или
, или ![]() .
(33)
.
(33)
Решаем (32) и (33) совместно: 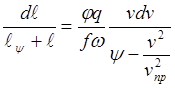 . (34)
. (34)
Решение уравнения (34) в 1903 г. дал профессор
Н.Ф.Дроздов. В качестве независимой переменной он принял величину ![]() . Тогда
. Тогда
. ![]() (35)
(35)
Для дальнейших преобразований воспользуемся уравнением (25),
подставив в него (35), тогда ![]() (36)
(36)
где ![]() (37)
(37)
Подставляя в (34) уравнения (28) и (36), после алгебраических преобразований находим
.
Обозначая ![]() (38)
(38)
и ![]() , (39)
, (39)
и подставляя 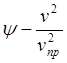 в (34),
получим
в (34),
получим ![]() (40)
(40)
Величина B называется параметром условий заряжания профессора Дроздова
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.