Уравнения состояния газа. Идеальный газ, реальный газ. Уравнение Нобля-Абеля (Дюпре), как следствие уравнения Ван-дер-Ваальса

Уравнения состояния газа. Идеальный газ, реальный газ. Формы (виды) уравнений состояния для газов. Уравнение Нобля-Абеля (Дюпре), как следствие уравнения Ван-дер-Ваальса.

Конкретная запись зависит от модели представления газа

·  Идеальный газ

·  Реальный газ

Идеальный – пренебрегаем объемом, занимаемым молекулами. Силами взаимодействия между молекулами тоже пренебрегаем.

Связь между давлением, плотностью и температурой описывается уравнением Клапейрона-Менделеева:     pW=wRT      или       p= rRT                                      (1)

где p – давление; W – объем; R=nr; n =1000/M - число молей газа в 1 кг пороха; М=23-25 г/моль; r=8,3143 КДж/(кг^.град) – универсальная газовая постоянная; Т – температура газа.

Формула (1) применяется для давлений до 50 МПа.

Реальный газ - Объем, занимаемый молекулами, учитывается, как и силы взаимодействия между молекулами

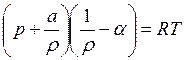Связь между давлением, плотностью и температурой описывается уравнениями Ван-дер-Ваальса, Нобля-Абеля (Дюпре) и вириальным.

Уравнение Ван-дер-Ваальса

(2)

где a – коэффициент, учитывающий сцепление между молекулами; a – коволюм газов (дм³/кг), параметр, равный учетверенному собственному объему молекул.

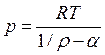Формула (2) применяется при давлениях в десятки тысяч МПа.

Уравнение Нобля-Абеля (Дюпре)                                                                                              (3)

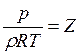Это частный случай уравнения Ван-дер-Ваальса, в котором параметром и пренебрегается. Формула (3) применяется при давлениях от 50 до 2000 МПа.

       Вириальное уравнение состояния                     ,   (4)

где                                                                                                (5)

Z – сжимаемость газа,  B, C, D и Е – вириальные коэффициенты, зависящие от температуры газа.

Физический смысл газовой постоянной

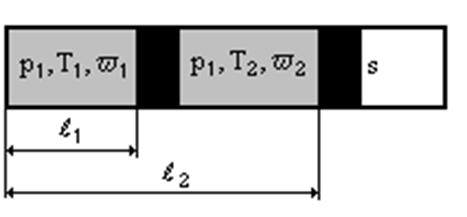
Идеальный поршень (поршень, при перемещении которого  не учитываются масса и сила  трения) при изменении параметров состояния  имеет  возможность  свободно перемещаться.  Для изменения начальных параметров состояния  нагреем  газ в  цилиндре при p₁=const на 1К. В результате поршень переместится из положения  I  в положение II. При перемещении  поршня будет совершена  работа A=p₁s(l₂-l₁). Так как sl₁=W₁, а sl₂=W₂ ,то  A=p₁(W₂-W₁) , и тогда A=R(T1+1) ,  т.е. R=A .

Таким образом, газовая постоянная R по физическому смыслу представляет собой механическую работу, совершаемую  единицей  массы  газа при его нагреве на 1К  и  расширении при p= const.   ИМЕННО НА 1 К!!

            Для использования уравнений состояния газов  необходимо знать в каждый  момент времени  массу образовавшегося газа        . Ее  количество  зависит от скорости газообразования при горении пороха.

Физическая картина горения пороха. Зоны горения.

Порох – это многкомпонентная  твердая система, способная гореть без доступа кислорода извне. Дымные пороха на открытом воздухе воспламеняются при температуре = 270-320 С, бездымные - при температуре около 200 C. Скорость воспламенения для дымных порохов составляет 1-3 м/с, для бездымных Порохов - 0,001-0,004 м/с.

Скорость горения дымных порохов  при нормальном давлении  составляет 1 мм/с,  пироксилиновых - 0,07 мм/с, нитроглицериновых-0,06-0,15 мм/c. Механизм горения порохового зерна может быть описан на микро-или макро уровнях. По сложившимся представлениям горение порохов может быть описано в виде  трех  основных  стадий:

1)  физических и химических структурно-фазовых превращений вещества, происходящих в тонком  поверхностном слое зерна;

2)  процессов превращения вещества в области, граничащей с поверхностным слоем;

3)  процессов  превращения промежуточных продуктов реакции в конечные продукты в гомогенной  газовой области, называемой зоной пламени.

Эти стадии в совокупности образуют пять характерных зон (рис.3): прогрева, физико-химических превращений - зону пиролиза, паро-газо-дымную, окислительно-восстановительных процессов ("темную" зону) и пламени.  (см.далее)

Фазы процесса горения пороха. Процесс образования окончательного состава газов.

Эти стадии в совокупности образуют пять характерных зон (рис.3): прогрева, физико-химических превращений - зону пиролиза, паро-газо-дымную, окислительно-восстановительных процессов ("темную" зону) и пламени.

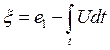
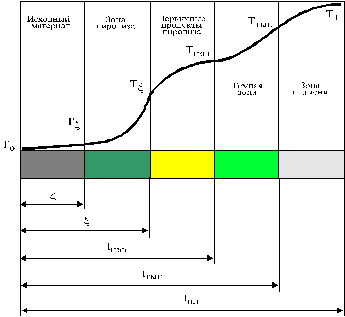 - подвижная координата, связанная с изотермой температуры начала разложения пороха (до  достижения условия            она равна половине толщины свода горения порохового зерна e₁ ;  - подвижная координата, зависящая от скорости  горения  и определяемая по уравнению