Решение системы уравнений методом Гаусса. Метод простых итераций. Процесс итераций для нахождения корней СЛАУ

СОДЕРЖАНИЕ

Задание 1                                                                                                               3

Задание 2                                                                                                               7

Задание 3                                                                                                             10

Задание 4                                                                                                             15

Список использованной литературы                                                                17

1.  Решить систему уравнений методом Гаусса

Исходные данные:

A=         =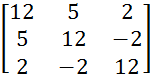

Перепишем систему уравнений в матричном виде и решим его методом Гаусса

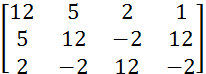
Получили единицу в 1-ом столбце, разделив 1-ую строку на 12

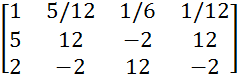
Для обнуления 1 элемента во 2-ой строке, от 2 строки отнимаем 1 строку, умноженную соответственно на 5.

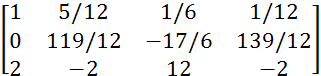
Для обнуления 1 элемента в 3-ей строке, от 3 строки отнимаем 1 строку, умноженную соответственно на 2.

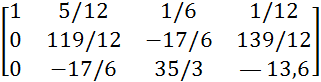
Для получения 1 на главной диагонали во 2-ой строке, разделим ее на 119/12.

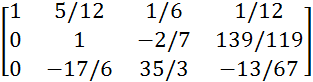
Для обнуления 2 элемента 3 строки, умножим ее на -17/6 и вычтем ее из 3.

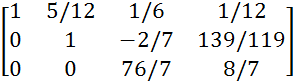
Для получения 1 на главной диагонали, разделим 3 строку на 76/7

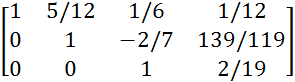
Закончился прямой ход метода Гаусса. Эта матрица соответствует системе:

 

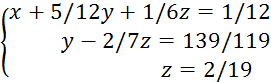
Последнее уравнение сразу даёт z =2/19.Подставляем найденное  z во второе уравнение и находим y, соответственно также находим и x.

Окончательно СЛАУ можно записать:

 

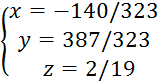
Определитель системы равен произведению тех элементов главной  диагонали, на которые мы делили строки:

=12*119/12*76/7=1292

Нахождение обратной матрицы методом Жордано-Гаусса относится к точным (прямым) методам.

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана.

После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A-1.

Запишем систему в виде:

A/E=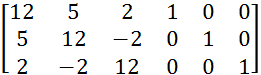

Последовательно будем выбирать разрешающий элемент, который лежит на главной диагонали матрицы. Разрешающий элемент равен 12.

На месте разрешающего элемента получаем 1, а в самом столбце  записываем нули.

Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент .

Получим 1, разделив 1 строку на 12.

A/E=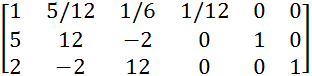

Помножим 1 строку на 5 и вычтем ее из 2 строки.

A/E=

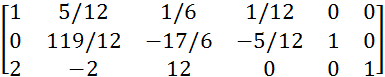
Умножим 1 строку на 2 и вычтем ее из 3-й строки.

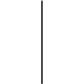A/E=

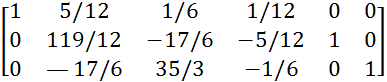
Разделим 2 строку на 119/12, для получения 1 во 2 столбце.

A/E=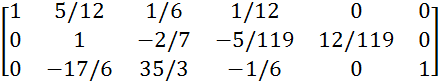

Получим 0 в 3 строке, умножив 2 строку на -17/6  и вычтем её из 3 строки.

A/E=

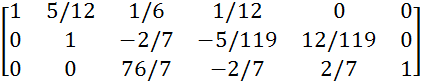
Разделим 3 строку на 76/7 и получим 1 на главной диагонали.

A/E=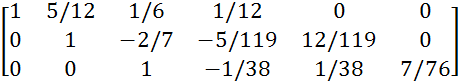

Закончился прямой ход метода Гаусса.  Начинаем обратный ход, в котором обнулим все элементы, лежащие  выше главной диагонали в левой подматрице.

Умножим 3 строку на -2/7, вычтем  её из 2 строки и получим:

A/E=

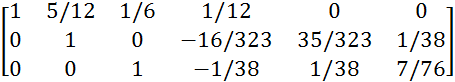
Умножим 2 строку на 5/12 и вычтем ее из 1 строки:

A/E=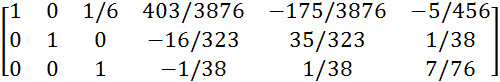

Умножим 3 строку на 1/6 и вычтем ее из 1 строки:

A/E=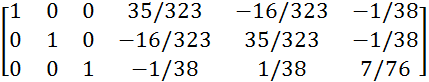

Процесс преобразования  (и обратный ход метода Гаусса тоже)  закончен. Та матрица, которая стоит в правой части расширенной матрицы  и есть искомая обратная матрица:

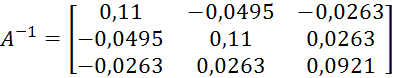
2.Решить систему линейных алгебраических уравнений методом простых итераций.

В= 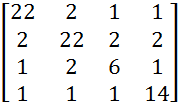      с = С заданной точностью   ε=10^-3 

Составим систему линейных уравнений

 

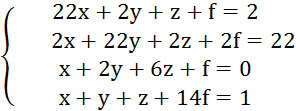
В данной системе уравнений, диагональные элементы оставим слева от знака равно, а все остальные перенесем вправо.

 

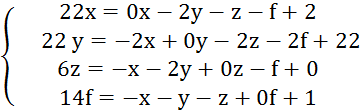
Разделим первую и вторую  строку на «22»,  третью на «6», четвертую на «14».

В= 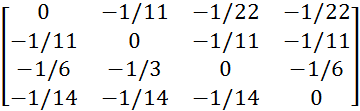      с =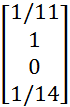

Вычислим норму матрицы В и вектора ß.

 

 

Так как норма матрицы В меньше 1, запишем итерационный процесс.

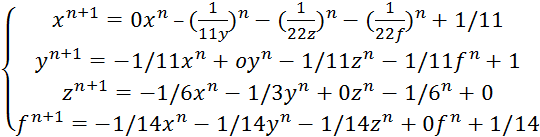                  (2.1)

Итерационный процесс будет сходиться к точному решению искомой системы. За начальный вектор возьмем x₁= ß,  получим:

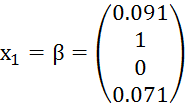                                                                                (2.2)

X₂  получается путем подстановки численного вектора  (1) во (2) систему линейных алгебраических уравнений.

 

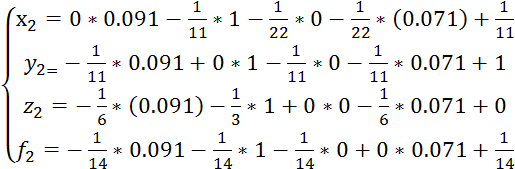
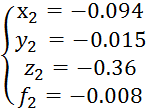
Оценим погрешность найденных значений вектора  х₂

                                                                                              (2.3)

= =0.496/(1-0.496 =0.983

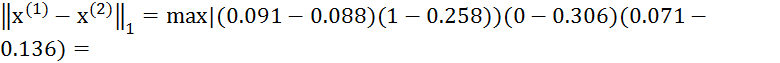=0.742

Проведем еще несколько итераций, процесс продолжается пока вычисляемая погрешность  не будет равна . Сведем данные в таблицу.

Таблица 2.1 - Процесс итераций для нахождения корней СЛАУ

	1	2	3	4	5	6	7
x	0,091	0,088	0,138	0,129	0,133	0,132	0,132
y	1,000	0,258	0,225	0,196	0,198	0,196	0,197
z	0,000	0,306	0,543	0,541	0,555	0,553	0,554
f	0,071	0,136	0,168	0,150	0,152	0,151	0,151
ε		0,9828326	0,487162	0,241472	0,119691	0,059327	0,029407
δ		0,742	0,033	0,029	0,003	0,002	0,0003

Процесс сходиться на 7 шаге, если подставить значения в компонент