Обратная задача теории упругости, страница 2

На задаваемые функции накладываются следующие ограничения:

1)  относительные деформации должны удовлетворять условиям сплошности (уравнениям Сен-Венана);

2)  перемещения должны быть непрерывными однозначными функциями во всех точках тела.

Рассмотрим три варианта задаваемых функций.

1)  Заданы упругие перемещения u, v, w. В этом случае простым дифференцированием из уравнений Коши (5) определяются деформации, а затем при помощи обобщенного закона Гука в форме (8) - напряжения. Уравнения совместности деформаций здесь всегда выполняются. Поверхностные силы можно найти из уравнений (3^*), а объемные – из дифференциальных уравнений равновесия Навье.

2)  Заданы относительные деформации. Они должны удовлетворять уравнениям Сен-Венана. По уравнениям обобщенного закона Гука (8) определяют напряжения, а перемещения находят интегрированием уравнений Коши (5). Поверхностные и объемные силы получают так же, как и в первом случае.

3)  Заданы напряжения. Деформации определяются при помощи (7). Далее все как во втором варианте.

При решении некоторых конкретных задач теории упругости иногда применяют полуобратный метод Сен-Венана. Суть его состоит в следующем. На основе существующих результатов решения близких или элементарных задач, на основе экспериментальных исследований – задают (предугадывают) часть искомых функций, совместных с полной системой уравнений теории упругости и рассматриваемой задачей. Если эту часть функций подставить в разрешающую систему уравнений, то задача существенно упростится за счет уменьшения числа искомых неизвестных. Решая такую упрощенную задачу, доопределяют неизвестную часть решения.

2.  Задание на выполнение расчетно-проектировочной работы.

Для стержня, рассматриваемого как трехмерное тело, заданы компоненты перемещения u,v и w в виде функций координат x,y,z (см. таблицу).

Требуется определить:

1)  соответствующие этим перемещениям деформации и напряжения;

2)  объемные силы;

3)  поверхностные силы по всем граням тела  (построить эпюру поверхностных сил по линии АВ;

4)  усилия в поперечном сечении стержня (построить эпюры усилий).

3.  Примеры

Ниже приведены примеры использования соотношений и формул теории упругости в последовательности, соответствующей ходу решения обратной задачи теории упругости.

3.1. Определение деформаций, соответствующих заданным перемещениям.

Пусть известные  функции перемещений имеют вид

;

.

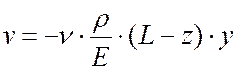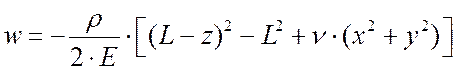Воспользуемся дифференциальными зависимостями Коши (5), для чего потребуется вычислить  частные производные от перемещений по координатам. Как известно, частная производная находится по правилам дифференцирования функции одной переменной, причем все остальные переменные рассматриваются при этом как постоянные.

Заданным перемещениям соответствуют следующие компоненты тензора деформаций:

;

;

.

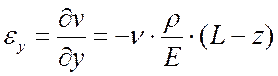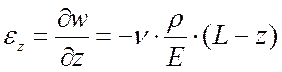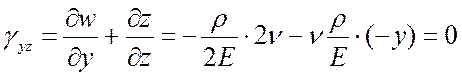3.2. Определение напряжений, соответствующих полученным выражениям для деформаций.

Пусть деформации рассматриваемого тела описываются функциями:

;           

;            ;

 ;                   .

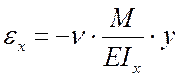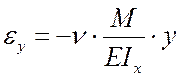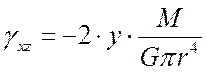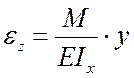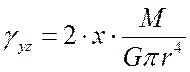Считаем материал линейно упругим и используем закон Гука в обратной форме (8). Предварительно вычислим объемную деформацию .

.

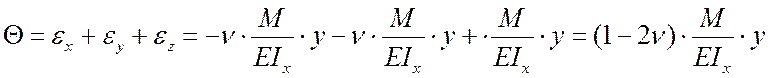Тогда компоненты тензора напряжений имеют вид:

;

;

;

;

.

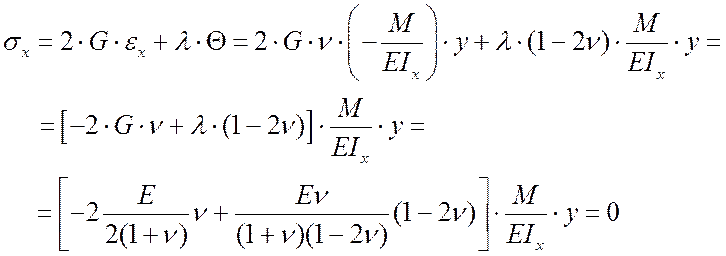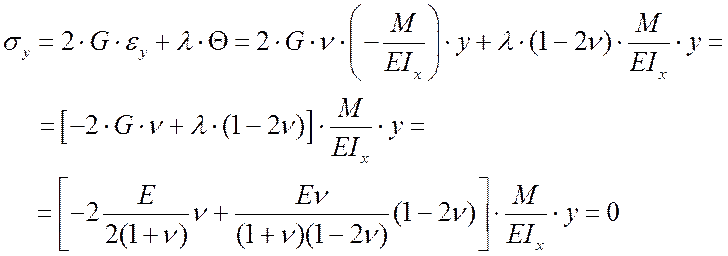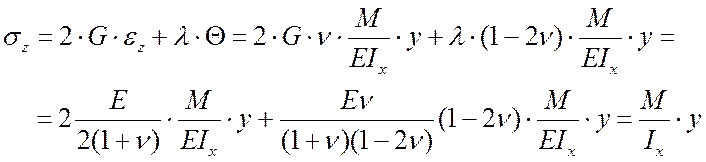
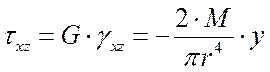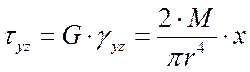3.3. Определение объемных сил.

Интенсивность объемных сил входит в дифференциальные уравнения равновесия Навье и, в частном случае, может быть равна нулю.

Пусть для напряжений, входящих во второе из уравнений (1), получены выражения

;      ;        .

Тогда

.

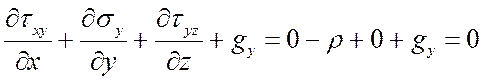
3.4. Определение поверхностных сил.

Интенсивность поверхностной нагрузки в проекциях на оси координат определяется с помощью уравнений равновесия элементарного тетраэдра (3^*). Эти вычисления должны быть произведены для каждого из элементов поверхности, для чего необходимо определить положение в пространстве граней рассматриваемого объекта. Ниже эта процедура показана на двух примерах.

Пример 1. Определим положение элементов поверхности трехгранной призмы (рис.2, a  ) и нагрузку на верхнем торце.

Рис. 2

Верхний и нижний торцы перпендикулярны оси Oy.

Для верхнего торца y = 0; направляющие косинусы нормали : , , .

Для нижнего торца y = L; направляющие косинусы нормали : , , .

Боковая грань с нормалью  (рис. 2,б) перпендикулярна оси Oz. Для нее z = a; направляющие косинусы нормали : , , .

Боковые грани с нормалями  и  (рис. 2,б) наклонны к осям Ox и Oz, координаты x и z точек этих граней определяют угол наклона α.

Для грани с нормалью  , направляющие косинусы нормали : , , .

Для грани с нормалью  , направляющие косинусы нормали : , , .

Вычисление поверхностной нагрузки покажем на примере верхнего торца для случая, когда тензор напряжений имеет вид

 .

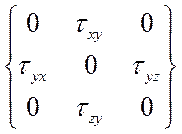Тогда: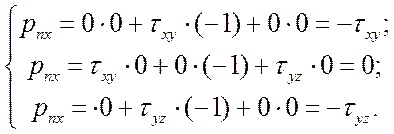                    

Вывод: верхний торец загружен поверхностными нагрузками, лежащими в плоскости торца.

Пример 2.  Определим положение в пространстве и нагрузку боковой поверхности цилиндра (рис.3) .

Рис.3

Координаты точек боковой поверхности цилиндра связаны соотношением . Направляющие косинусы нормали : , , .

Пусть напряженное состояние тела описывается тензором

.

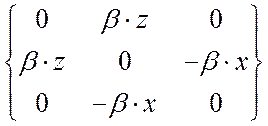Тогда

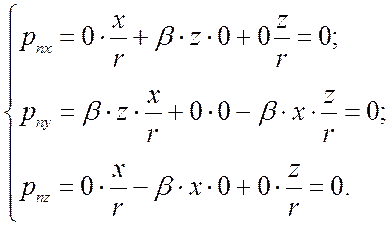
Вывод: боковая поверхность свободна от нагрузки.

3.5. Определение усилий в поперечных сечениях

Усилия в поперечных сечениях представляют собой, как известно, составляющие главного вектора и главного момента внутренних сил. Усилия связаны с напряжениями (т.е. с интенсивностью внутренних сил) условиями статической эквивалентности (4).

Таким образом, определение усилий связано с вычислением двойного интеграла по площади поперечного сечения от функции двух переменных, которое сводится к последовательному вычислению двух простых интегралов.

Покажем выполнение этих действий на двух примерах.

Пример 1.  Пусть касательные напряжения в сечении стержня с осью Oy равны

Вычислим крутящий момент , интегрируя по треугольному сечению (рис.4):

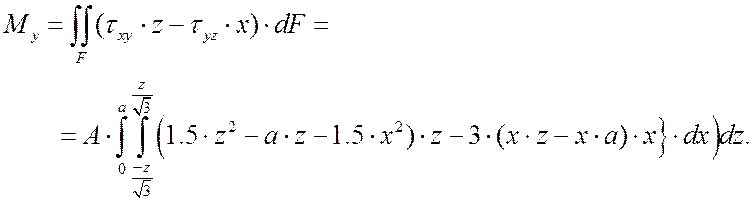
Внутренний интеграл:

.

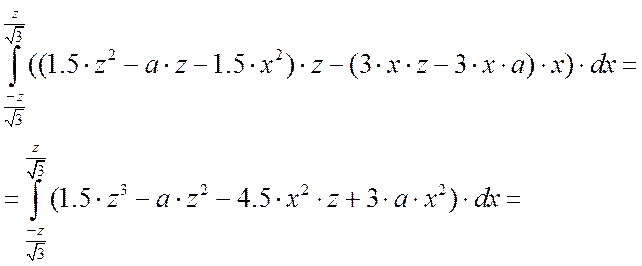
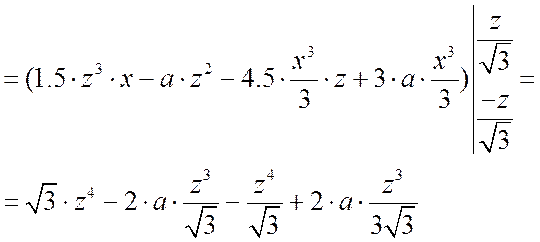Рис.4

Тогда

.

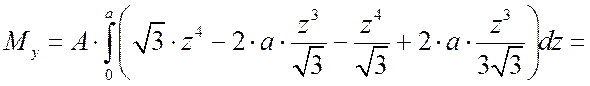
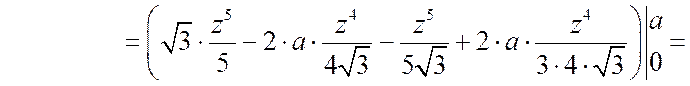
Пример 2. Пусть касательные напряжения в сечении стержня с осью Oz равны

.

Вычислим крутящий момент , интегрируя по сечению произвольной формы:

.

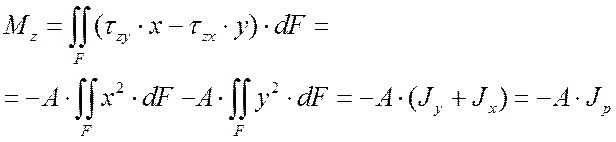Здесь использовались формулы, определяющие понятия осевой ( и ) и полярный () моменты инерции.

Для конкретного вида поперечного сечения следует провести дальнейшие вычисления, выразив соответствующие геометрические характеристики поперечных сечении через заданные размеры.

В других случаях при интегрировании  окончательные формулы могут содержать выражения, определяющие понятия статического момента, центробежного момента, площади. Полезно вспомнить, что статический момент относительно оси, проходящей через центр тяжести, равен нулю. Центробежный момент инерции относительно главных осей также равен нулю.

Таблица

1
2
3
4

5
6
7
8

9
10
11
12

13
14
15
16

17
18
19
20

21		; ; , где
22		; ; , где
23		; ; , где
24