Исследование динамических характеристик магнитных материалов. Семейство петель гистерезиса при изменении Hm, страница 5

S - площадь поперечного сечения магнитопровода, (S=2,4·10^-4   м² ).

Знак минус в выражении опущен, т.к. в рассматриваемом случае это не имеет значения.

Из приведённого соотношения (4) видно: для того, чтобы напряжение, приложенное к вертикально отклоняющим пластинам одного из двух каналов осциллографа С1-83, было пропорционально индукции в магнитопроводе, необходимо проинтегрировать ЭДС е₂ во времени.

В качестве простейшей итерирующей цепочки обычно применяют R-Cцепочку (рис.3).

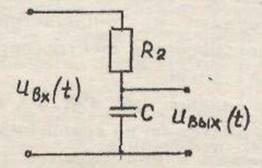
Рис. 3.   Схема простейшей интегрирующей цепочки

Для получения необходимой точности интегрирования нужно, чтобы активное сопротивление схемы было больше реактивного .

Тогда ток в контуре можно считать активным. Учитывая, что входное напряжение интегратора равно

                     (5)

то выходное напряжение интегратора будет равно

                 (6)

то есть к вертикально отклоняющим пластинам одного из каналов осциллографа подводится напряжение, пропорциональное магнитной индукции В.

При одновременном приложении напряжения U_вых и U₁к соответствующим клеммам осциллографа, на его экране возникает кривая, характеризующая зависимость магнитной индукции В от напряженности магнитного ноля H, то есть будет наблюдаться динамическая петля гистерезиса.

Преимущество метода состоит в том, что он даёт возможность не только изучить динамические характеристики магнитомягких материалов, но также визуально наблюдать и исследовать влияние на эти характеристики различных факторов (деформации, температуры, подмагничивания и т.д.). Метод отличается также малой трудоемкостью и быстротой измерения.

Определение масштаба по вертикальной оси

Действующее значение ЭДС Е₂, индуктируемой на зажимах измерительной обмотки при синусоидальной кривой B=f(t), связано с магнитной индукцией в мягнитопроводе следующим соотношением

E₂=4,44W₂fSB_m                      (7)

где W₂- число витков измерительной обмотки;

f - частота переменного тока, (f=50 Гц);

B_m - заданное значение амплитудного значения индукции в магнитопроводе, (B_m=0,6 Тл);

Задавшись удобным значением магнитной индукции в магнитопроводе, например 0,6 Тл, вычисляем по формуле (7) действующее значение ЭДС Е₂, и собрав схему (рис.2), расчетное значение ЭДС Е₂ подают на вход интегратора. Значение ЭДС Е₂устанавливают с помощью ЛАТРа по вольтметру Vи в этом случае индукция в магнитопроводе B_m  будет равна заданной.

Вертикальная координата вершины петли гистерезиса У в делениях шкалы осциллографа будет соответствовать заданной магнитной индукции B_m. Отсюда масштаб по вертикальной оси можно определить по формуле

                 (8)

где т_В -масштаб по магнитной индукции (Тл/дел.);

В_т - заданное значение магнитной индукции (Тл);

У - вертикальная координата вершины петли гистерезиса при расчетном значении Е₂ (дел.).

Определение масштаба по горизонтальной оси

Для определения масштаба но горизонтальной оси можно воспользоваться соотношением для действующего значения тока в первичной обмотке I₁и уравнением (2)

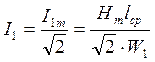                          (9)

где H_m -  амплитудное значение напряженности магнитного поля в магнитопроводе (А/м), задается величиной, удобной для расчета.

Задавшись удобным значением напряженности магнитного поля в магнитопроводе (например 1000А/м), вычисляют по формуле (9) действующее значение тока намагничивания I₁ и, собрав схему (рис.2), устанавливают расчетное значение тока I₁ с помощью ЛАТРа по миллиамперметру mА. В этом случае напряженность магнитного поля в магнитопроводе H_m будет равна заданной. Горизонтальная координата вершины петли гистерезиса X в делениях шкалы осциллографа будет соответствовать заданному значению Н_т. Отсюда масштаб по горизонтальной оси можно определить по формуле

                           (10)