Схема автоматизации производства сухого хлористого водорода. Классификация потенциометрических преобразователей

погрешность почти не зависит от нагрузки при малых значениях входного сигнала х (рис. 2.9, а, г);

погрешность всех датчиков возрастает при уменьшении сопротивления нагрузки, или снижении коэффициента нагрузки  (рис. 2.9);

у датчиков, собранных по схемам рис. 2.4, в, г, при крайних положениях токосъемников погрешность отсутствует (рис. 2.9, в, г). Датчики же, имеющие один токосъемник (см. рис. 2.4, а, б), при крайнем его положении дают определенную погрешность (рис. 2.9, а, б);

с возрастанием величины относительной ошибки  коэффициент преобразования датчика снижается. Это следует из соотношения (2.1), поскольку значение выходного напряжения U_выхуменьшается на величину абсолютной ошибки .

Первая особенность обусловлена тем, что из-за наличия средней точки в схемах рис. 2.4, а, г сопротивление потенциометра со стороны выхода обращается в малую величину, близкую к нулю, если токосъемники находятся в окрестности средней точки. В связи с этим при любом значении R_н относительная ошибка будет стремиться к нулю (2.6), поскольку сопротивление потенциометра со стороны выхода .

Отсутствие погрешности в схемах рис. 2.4, в, г при крайнем положении токосъемников объясняется тем, что в этом положении сопротивление нагрузки R_Hподключается непосредственно к источнику питания, имеющему малое сопротивление. Таким образом, сопротивление потенциометра со стороны выхода становится равным сопротивлению источника питания и, следовательно, коэффициент нагрузки  становится очень большим, а ошибка  - близкой к нулю. Для схем рис. 2.4, а, б с одним токосъемником значение сопротивления потенциометра со стороны выхода не может стать меньше 0,5R, поэтому ошибка  имеет некоторое конечное значение при крайнем положении токосъемника.

ДИНАМИЧЕСКИЕ СВОЙСТВА ЛИНЕЙНЫХ ПОТЕНЦИОМЕТРИЧЕСКИХ ДАТЧИКОВ.

Для характеристики динамических свойств потенциометрических датчиков определим их передаточную функцию. Входной величиной датчика является перемещение x. За выходную величину можно принять напряжение на нагрузке или ток через нее. Обычно удобнее в качестве выходной величины рассматривать ток в нагрузке, который определяется на основании теоремы об эквивалентном генераторе (рис. 2.10) [45]:

, где   Z_H -  комплексное   сопротивление   нагрузки; R_вн  - внутреннее сопротивление эквивалентного генератора.

Рассмотрим два случая.

Чисто активная нагрузка, т.е. Z_H = R_H, тогда

, так как G_вых0= к₁х.

Применяя преобразование Лапласа, получим

.

Таким образом, потенциометрическийизмерительный преобразователь при чисто активной нагрузке является безинерционным усилительным звеном (1.52). Следовательно, все частотные и временные динамические характеристики усилительного звена (табл. 1) полностью описывают динамические свойства потенциометрических датчиков с активной нагрузкой.

Индуктивная нагрузка с наличием активной составляющей.Для эквивалентной цепи (рис. 2.10) можно записать

,

Применяя преобразование Лапласа, получим

.

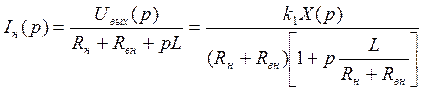Обозначим , а , тогда

.

Следовательно, при индуктивном характере нагрузки нагруженный потенциометр следует рассматривать как инерционное звено (1.54) и распространять на него все динамические свойства этого звена (1.56) — (1.60) (см. табл. 2).

Часто инерционность датчика, создаваемую нагрузкой, относят не к самому датчику, а к входной цепи элемента, подключенного на выход этого датчика. При этом подходе потенциометрический датчик всегда рассматривается как безинерционное звено (см. табл. 1).

В случае, когда статическая характеристика потенциометрического измерительного   преобразователя  обладает одним из отмеченных типов существенных нелинейностей (см. табл. 9, п. 1, п. 6, п. 9), динамические свойства этого элемента будут изменяться, вследствие чего появляются нелинейные искажения выходного сигнала, которые не учитываются линейным представлением (2.2) потенциометрического измерительного преобразователя. Учесть это явление можно, воспользовавшись математическим аппаратом для описания нелинейных элементов, предложенным в п. 1.3, принимая во внимание, что рассматриваемый элемент всегда сочленяется с другими элементами, математические модели которых представляют собой инерционные звенья, обладающие свойствами фильтра низких частот. Следовательно, справедливо предположение, положенное в основу метода