


















1. ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ И
КИНЕМАТИЧЕСКИХ ПАРАМЕТРОВ ПРИВОДА
Требуемая мощность электродвигателя [1, с. 23]
Ртр = F · V / hо
где V, м · с-1 ; F, кН; Ртр, кВт; hо - КПД привода
hо = hк · hц · hп4
hк = 0,96 – КПД конической зубчатой передачи;
hц = 0,97 – КПД цилиндрической зубчатой передачи;
hп = 0,99 – КПД одной пары подшипников качения;
![]() hо = 0,96 · 0,97 · 0,99 4 = 0,8945
hо = 0,96 · 0,97 · 0,99 4 = 0,8945
![]() Ртр= 10*1/0,8945 = 11 кВт
Ртр= 10*1/0,8945 = 11 кВт
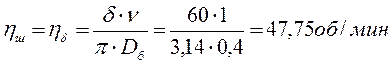 Частота вращения тихоходного вала
редуктора равна частоте вращения вала барабана:
Частота вращения тихоходного вала
редуктора равна частоте вращения вала барабана:
Выбираем асинхронный электродвигатель серии 160S6 N=11 кВт с nс=1000 об/мин, скольжением S = 2,7 %. Частота вращения вала электродвигателя:
nдв = nб * uпр.max =954 об/мин
Требуемое передаточное отношение редуктора:
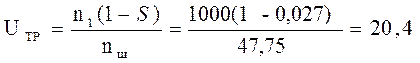
Uр = 20 ; Uб = U1 = 4; Uт = U2 = 5
n1= 973 об/мин
n2= n1 / U1 = 973/4 = 243,2 об/мин
n3 = n2 / U2 = 243,2/5 = 48,7 об/мин
Мощности и крутящие моменты, передаваемые валами:
Р1 = Ртр = 11 кВт
Р2 = Р1 · hк · hп = 11 · 0,96 · 0,99 = 10,67 кВт
Р3 = Р2 · hк · hп = 10,67 · 0,96 · 0,99 = 10,35 кВт
Т1 = 9550 · Р1 / n1 = 9550 · 11/973 = 108 Н·м
Т2 = 9550 · Р2 / n2 = 9550 · 10,67/243,2 = 419 Н·м
Т3 = 9550 · Р3 / n3 = 9550 · 10,35/48,7 = 2029,6 Н·м
2. РАСЧЕТ КОНИЧЕСКОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ
БЫСТРОХОДНОЙ СТУПЕНИ
2.1. Выбор материалов и допускаемые напряжения.
Выбираем для шестерни сталь 40Х с термообработкой улучшение, а для колеса - сталь 45. Их механические характеристики определяем по табл.1[3]. Для шестерни твердость поверхности зуба НВ1 - 269 … 302 ,δ=780, Nho = 23.5; для колеса принимаем вид термообработки – улучшение, тогда НВ2 - 235… 262 δ=700, Nho = 16.8.
Допускаемые контактные напряжения
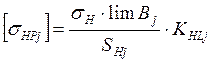 (1)
(1)
где j = 1 для шестерни и j = 2 для колеса, ![]() - предел контактной выносливости поверхности зубьев,
соответствующий базовому числу циклов перемен напряжений, определяется в
зависимости от марки стали и ее химико-термической обработки по табл. 2; KHLj – коэффициент долговечности; SH = 1,1 для колес с однородной
структурой материала, SH=1,2 - при поверхностном упрочнении зубьев.
- предел контактной выносливости поверхности зубьев,
соответствующий базовому числу циклов перемен напряжений, определяется в
зависимости от марки стали и ее химико-термической обработки по табл. 2; KHLj – коэффициент долговечности; SH = 1,1 для колес с однородной
структурой материала, SH=1,2 - при поверхностном упрочнении зубьев.
Для шестерни SH1 = 1,2; для колеса SH1 = 1,1. Предел контактной выносливости для шестерни:
sH Lim b1 =(2*HB1ср + 70)= 2*285.5+70=641 МПа для колеса:
sH Lim b2 = (2*HВ2ср + 70) = 2 · 248.5 + 70 =567 МПа
Коэффициент долговечности равен
![]()
где NHE j – эквивалентное число циклов напряжений;
NHO j – базовое число циклов, определяемое в зависимости от твердости по Бринелю или Роквеллу,
![]()
![]()
![]() - коэффициент режима
работы,
- коэффициент режима
работы, ![]()
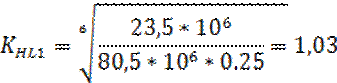
![]()
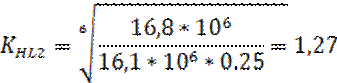
![]()
![]()
![]()
Принимаю
для зубчатой передачи допускаемое напряжение ![]() Мпа
Мпа
Допускаемые напряжения изгиба
![]()
Пределы изгибной выносливости зубьев:
![]()
![]()
Коэффициенты
безопасности при изгибе : ![]()
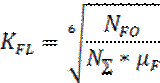
![]() - коэффициент
эквивалентности,
- коэффициент
эквивалентности,
![]() - базовое число циклов при
изгибе,
- базовое число циклов при
изгибе,
![]()
Принимаю
![]()
![]()
Коэффициенты,
учитывающие влияние двухстороннего приложения нагрузки, для нереверсивного
привода ![]()
![]()
![]()
2.2 ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ ПЕРЕДАЧ
При проектном расчете конической зубчатой передачи в качестве ее основного геометрического параметра определяют ориентировочно внешний делительный диаметр колеса из условия обеспечения контактной выносливости рабочего профиля зуба колеса по формуле:
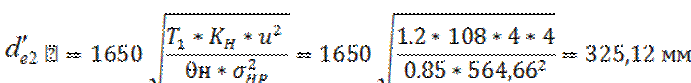
![]() =1,2 –
ориентировочное значение коэффициента нагрузки;
=1,2 –
ориентировочное значение коэффициента нагрузки;
qн - коэффициент, учитывающий вид конической передачи.
Величину qн для конических колес с прямыми зубьями принимают равной qн = 0,85;
Ориентировочно определяем число зубьев колеса [5, с.4]
me=1,36*105*108*4/3552*309,53*0,85=1,77 мм
Принимаем модуль me=2мм
Z2=de2/me=355/2=177,5
Z1=Z2/u=44,25
Округляем Z1=44 и Z2 = 177.
Вычисляем с точностью до четвертого знака после запятой фактическое значение передаточного числа
Uф1=Z2/Z1=4,022
его отличие от номинального передаточного числа равно:
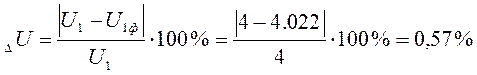
de2= Z2*me=177*2=354мм
de1= Z1*me=44*2=88мм
Определяем углы делительных конусов с точностью не ниже 1² [5,с.5].
![]()
![]()
Для выравнивания удельных скольжений в зацеплении шестерню рекомендуется выполнять с положительным радиальным смещением, а колесо с равным ему по абсолютной величине отрицательным смещением
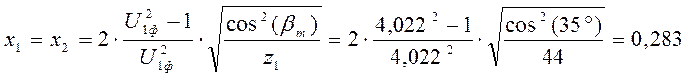
Здесь bm - угол наклона зуба. обычно угол bm выбирают кратным 5°.
Определяем внешнее конусное расстояние [5, с.5]
Re=de1/2sinδ1=182,57 мм
Ширина шестерни и колеса
b1’ = b2’ = y’br · R’e = 0,285 · 182,6 = 52,033 мм
Округляем b’1 и b’2’ до ближайшего значения из ряда Rа 40 [1, c. 127] по табл. 9;
b1 = b2 = 53 мм
Уточняем значение коэффициента ширины зубчатого венца:
y br’ = b2 / Re = 53 / 182,57 = 0,29
Определяем средний диаметр шестерни:
![]() 354 · (1-0,5 · 0,285) / 4,022= 75,227
мм
354 · (1-0,5 · 0,285) / 4,022= 75,227
мм
Вычисляем окружную скорость на среднем диаметре:
V = p · dm1 · n1 / (6 ·104 ) = 3,14 · 75,227 · 973 / (6 · 104) = 3,831 м/с
Степень точности конических передач: nст = 7
2.3. Проверочный расчет передачи.
Определяем контактные напряжения [5, с.6]
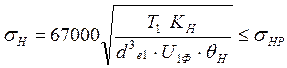 (4)
(4)
где KH = KHb · KHn
KHn - определяем по табл. 15,1; KHn = 1,187
KHb = 1+0,09*yt*Cп*u3![]() =1,074
=1,074
При yt=1 (HB≤350)
KH = 1,187*1,074=1,275
Вычисляем sн по формуле (4)
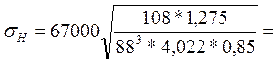 515,095 МПа < 660 МПа
515,095 МПа < 660 МПа
Определяем:
![]() = 8,77 %
= 8,77 %
Допускаются превышения напряжений sн над sнр не более чем на 15%.
Проверяют зубья шестерни и колеса на выносливость по напряжениям изгиба, использую формулы [5, с.7]
 (5)
(5)
q F = 0,85
Коэффициент нагрузки определяется по формуле: [5, с. 7]
KF = KFb · KFn = 1,359
где ea - коэффициент перекрытия для передач с круговыми зубьями ea = 1,3;
KFb = 0,18 + 0,82 *KНb = 1,061
KFn находим по выражению:
KFn = 1 + 1,5· (KHn - 1) = 1,281
Коэффициент формы зуба
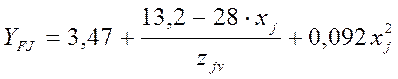
где Zjv - эквивалентное число зубьев, определяется по формуле
Zjv = Zj / (cos dj )
Z1v = Z1 / (cos d1 ) = 45,36
Z2v = Z2 / (cos d2) = 734,44
![]()
![]()
Определяем sF1 по формуле (5)
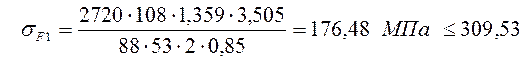
sF2 = 176,48 · 3,593 / 3,505 = 180,91 < 323,8 МПа
2.4 Определение сил в конической зубчатой передаче
Fа1 = Ft1 · tgα*sinδ = 252,12 Н
Радиальная сила на шестерне для первого случая:
Fr1 = Ft1 · tgα*cosδ =1014,2 Н
Осевая и радиальная силы на колесе соответственно равны:
Fа2 = Fr1 = 1014,2 Н Fr2 = Fа1 = 252,12 Н
3. РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ ТИХОХОДНОЙ СТУПЕНИ
Выбираем для шестерни сталь 45 с термообработкой улучшение, а для колеса - сталь 40. Их механические характеристики определяем по табл.1[3]. Для шестерни твердость поверхности зуба НВ1 - 235 … 262 ,δ=780, Nho = 16,8; для колеса принимаем вид термообработки – улучшение, тогда НВ2 - 192… 228 δ=700, Nho = 11,2.
В этом случае при расчете допускаемых контактных напряжений по формуле (1):
![]()
![]()
![]() - коэффициент режима
работы,
- коэффициент режима
работы, ![]()
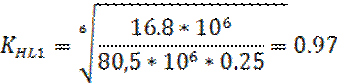
Принимаю
![]() =1,0
=1,0
![]()
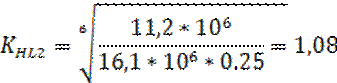
![]()
![]()
![]()
Принимаю
для зубчатой передачи допускаемое напряжение ![]() Мпа
Мпа
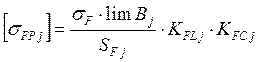 Допускаемые напряжения изгиба:
Допускаемые напряжения изгиба:
Пределы изгибной выносливости зубьев:
![]()
![]()
Коэффициенты
безопасности при изгибе : ![]()
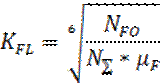
![]() - коэффициент
эквивалентности,
- коэффициент
эквивалентности,
![]() - базовое число циклов при
изгибе,
- базовое число циклов при
изгибе,
![]()
Принимаю
![]()
![]()
Коэффициенты,
учитывающие влияние двухстороннего приложения нагрузки, для нереверсивного
привода ![]()
![]()
![]()
3.2. Определение геометрических размеров передачи
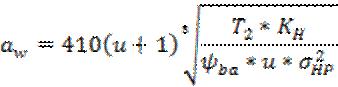
yBA – коэффициент ширины венца по межосевому расстоянию, который выбирают из единого ряда, рекомендованного ГОСТ 2185-66 [7табл. 12] с учетом расположения опор относительно зубчатого венца;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.