СОДЕРЖАНИЕ
РЕФЕРАТ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1. Уравнение Бернулли . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2. Центробежные Насосы. . . . .. . . . . . . . . . . . . . . . . . . . 5
2.1. Исходные Данные . . . . . .. . . . . . . . . . . . . . . . . . . . . 12
2.2. Гидравлический Расчет. . . . .. . . . . . . . . . . . . . . . . . . . . 12
ЗАКЛЮЧЕНИЕ . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . 14
БИБЛИОГРАФИЧЕСКИЙ СПИСОК . . . . . . . . . . . . . . . . . . . . . 15
РЕФЕРАТ
В данной курсовой работе будет произведен гидравлический расчет насоса по заданным параметрам с учетом концентраций и вязкостью транспортируемой среды, а также температуры. После расчета с учетом всех условий и параметров будет выбран насос.
Необходимо, чтобы выбранный насос обеспечивал систему необходимым расходом и напором, большим, чем требуемый. Это позволит в случае необходимости расположить приемные емкости несколько выше указанного уровня.
Кроме того, в теоретической части лабораторной работы, будет произведено ознакомление с физическим смыслом уравнения Бернулли.
Также в данной курсовой работе представлены различные центробежные насосы и рассмотрен принцип их действия и их характеристики.
ВВЕДЕНИЕ
Цель работы – разработка трубопроводной системы для подачи 60% раствора серной кислоты (30 м3/час) в аппарат, расположенный на высоте 12 м. Количество поворотов трубопровода на 90° – 6 штук. Длина нагнетательный линии-70 м. Длина всасывающей линии – 2 м. Высота всаса – 0,5 м.
Необходимо подобрать материал и размер трубы, разработать пневмогидравлическую схему в узлах транспортировки кислоты и выбрать нужный насос.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1. Уравнение Бернулли.
Движение жидкости, как и движение любых других физических тел, подчиняется фундаментальным законам механики, в частности, закону сохранения энергии. В силу особых свойств жидкости – её текучести – законы, описывающие её поведение, отличаются от законов для тел фиксированной формы.
Уравнение Бернулли для струйки идеальной жидкости [1]
Для идеальной жидкости закон сохранения энергии определяется уравнением Бернулли, в соответствии с которым при стационарном безвихревом движении несжимаемой жидкости гидравлическая высота, равная сумме геометрической, пьезометрической и скоростной высот, сохраняет постоянное значение во всей области течения.
В струйке идеальной жидкости трение и скорость потока по сечению постоянна, т.е. V=Vср.
Примем следующие допущения:
1) жидкость идеальная (невязкая, несжимаемая);
2) поток установившийся.
На основании закона сохранения энергии можно записать, что изменение кинетической энергии элементарного объема жидкости при его движении равно изменению потенциальной энергии, обеспечиваемой нивелирной высотой z и давлением р.
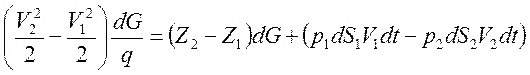
Разделив обе части этого уравнения на dG получим
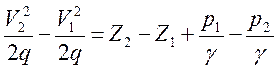 , или
, или
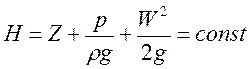 , где Н – гидравлическая
высота(полный напор); P – давление жидкости, Па;
, где Н – гидравлическая
высота(полный напор); P – давление жидкости, Па; ![]() - плотность
жидкости, кг/
- плотность
жидкости, кг/![]() ; W –
скорость течения, м/с; g – ускорение свободного падения, м/
; W –
скорость течения, м/с; g – ускорение свободного падения, м/![]() ;
;
Z – геометрическая высота, м.
Величина
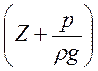 называется
статическим напором. Она представляет собой потенциальную удельную, отнесенную
к единице веса, энергию жидкости, а скоростной (динамический) напор
называется
статическим напором. Она представляет собой потенциальную удельную, отнесенную
к единице веса, энергию жидкости, а скоростной (динамический) напор
![]() - удельную
кинетическую энергию.
- удельную
кинетическую энергию.
Таким образом, уравнение Бернулли является выражением закона
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.