Действие вертикальной сосредоточенной силы, приложенной к поверхности упругого основания. Напряжения в грунте от одной сосредоточенной силы

П Р И М Е Р Ы

решения задач по курсу

«механика грунтов»

Теоретическая часть

При действии вертикальной сосредоточенной силы, приложенной к поверхности упругого основания (рис. 13, а), вертикальные напряжения в точке М определяют по формуле

   ,    (1.18)

где  - безразмерный коэффициент, зависящий от соотношения ;  - вертикальная сосредоточенная сила;  - вертикальная координата точки М.

Значения коэффициента при различных соотношениях r/zприведены в табл. 1.8.

При действии нескольких сосредоточенных сил (рис. 1.13,б) напряжения в точке М определяют с помощью обычного суммирования:

. (1.19)

Напряжения, возникающие в грунтах под центром прямоугольной площади загружения равномерно распределенной нагрузкой, находят по формуле

, (1.20)

где  - коэффициент рассеивания напряжений, определяемый по таблице 1.9 в зависимости от соотношения  и  (здесь  и  - соответственно ширина и длина прямоугольника); - равномерно распределенное давление.       

Используя данные табл. 1.9, можно определять вертикальные напряжения и в угловых точках прямоугольной площади загружения по формуле

 (1.21)

с той лишь разницей, что значение  принимается равным .

Для определения напряжений в любой точке внутри загруженной области или вне ее используют метод угловых точек (рис. 1.14). Если напряжения определяют в точке, находящейся под нагруженной площадью (см. рис. 1.14,а), то загруженную площадь разбивают на четыре прямоугольника I, II, IIIи IV, для каждого из которых точка М является угловой, и напряжения находят как сумму давлений под угловыми точками четырех площадей загружения:  

                                 . (1.22)

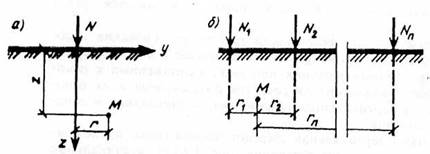
Рис. 1.13. Напряжения в грунте от одной сосредоточенной силы (а)

и нескольких сосредоточенных сил (б)

Таблица 1.8. Значения коэффициента

0	0,4775	0,8	0.1386	1.6	0.02
0,1	0,4657	0,9	0.1083	1.7	0.016
0,2	0,4329	1,0	0.0844	1.8	0.0129
0,3	0,3849	1,1	0.0658	1.9	0.0105
0,4	0,3294	1,2	0.0513	2.0	0.0085
0,5	0,2733	1,3	0.0402	2.5	0.0034
0,6	0,2214	1,4	0.0317	3.0	0.0015
0,7	0,1762	1,5	0.0251	4.0	0.0004

Таблица 1.9. Значения коэффициента       

	для фундаментов
	прямоугольных при								ленточных при
	1	1.4	1.6	1.8	2.4	3.2	4	5
0,4	0,960	0,972	0,972	0,975	0,976	0,977	0,977	0,977	0,977
0,8	0,800	0,848	0,859	0,866	0,875	0,879	0,880	0,881	0,881
1,2	0,606	0,682	0,703	0,717	0,740	0,749	0,753	0,754	0,755
1,6	0,449	0,532	0,558	0,578	0,612	0,630	0,636	0,639	0,642
2	0,336	0,414	0,441	0,463	0,505	0,529	0,540	0,545	0,550
2,4	0,257	0,325	0,352	0,374	0,419	0,449	0,462	0,470	0,477
2,8	0,201	0,260	0,284	0,304	0,350	0,383	0,400	0,410	0,420
3,2	0,160	0,210	0,232	0,25 1	0,294	0,329	0,348	0,360	0,374
3,6	0,130	0,173	0,192	0,209	0,250	0,285	0,305	0,320	0,337
4	0,108	0,145	0,161	0,176	0,214	0,248	0,270	0,285	0,306
4,4	0,091	0,122	0,137	0,150	0,185	0,218	0,239	0,256	0,280
4,8	0,077	0,105	0,118	0,130	0,161	0,192	0,213	0,230	0,258
5,2	0,066	0,091	0,102	0,112	0,141	0,170	0,191	0,208	0,239
5,6	0,058	0,079	0,089	0,099	0,124	0,152	0,172	0,189	0,223
6	0,051	0,070	0,078	0,087	0,110	0,136	0,155	0,172	0,208
6,8	0,040	0,055	0,062	0,069	0,088	0,110	0,128	0,144	0,184
7,6	0,032	0,044	0,050	0,056	0,072	0,091	0,107	0,123	0,166
8,4	0,026	0,037	0,042	0,046	0,060	0,077	0,091	0,105	0,150
9,2	0,022	0,031	0,035	0,039	0,051	0,065	0,078	0,091	0,137
10	0,019	0,026	0,030	0,033	0,044	0,056	0,067	0,079	0,126
12	0,015	0,020	0,024	0,026	0,034	0,044	0,051	0,060	0,104

Если же точка М находится вне пределов площади загружения АBCD(см. рис. 1.14,6), она считается угловой для четырех фиктивных площадей загружения I, II, III и IV (прямоугольники АЕМК, KMGD, BEMF и FMGC). При этом в пределах площадей I и II направление фиктивной нагрузки совпадает с направлением исходной нагрузки, а в пределах площадей III и IV направление фиктивной нагрузки является обратным направлению исходной нагрузки, и напряжения находят по выражению

 (1.23)

Для распределенной полосовой нагрузки, изменяющейся по закону треугольника (см. рис. 1.14,в), вертикальные напряжения в толще основания определяются по формуле

, где  - коэффициент, зависящий от соотношения  и , и определяемый по таблице 1.10.

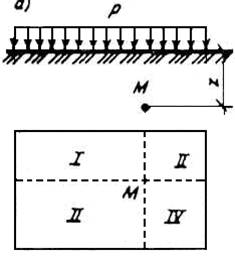
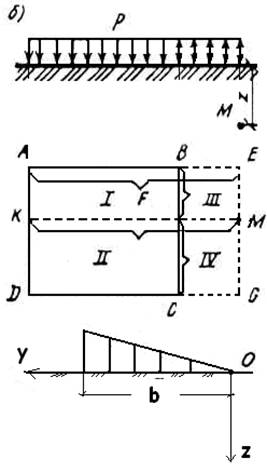
Таблица 1.10. Коэффициент  для треугольной нагрузки

	при
	-1,05	-1	-0,5	0	0,25	0,5	0,75	1	1,5	2	2,5
0	0	0	0	0	0,25	0,5	0,75	1	0	0	0
0,25	0	0	0	0,08	0,26	0,48	0,64	0,42	0,02	0	0
0,5	0	0	0,02	0,13	0,26	0,41	0,48	0,35	0,06	0,02	0
0,75	0,01	0,02	0,04	0,15	0,25	0,34	0,36	0,29	0,11	0,02	0,01
1	0,01	0,03	0,06	0,16	0,22	0,28	0,28	0,24	0,13	0,04	0,01
1,5	0,02	0,05	0,1	0,14	0,18	0,2	0,2	0,18	0,12	0,06	0,04
2	0,03	0,06	0,09	0,13	0,15	0,16	0,16	0,15	0,11	0,07	0,05
3	0,05	0,06	0,08	0,1	0,1	0,1	0,11	0,1	0,09	0,07	0,05
4	0,05	0,06	0,07	0,08	0,08	0,09	0,08	0,08	0,07	0,06	0,05
5	0,05	0,05	0,06	0,06	0,06	0,06	0,07	0,06	0,06	0,05	0,05
6	0,04	0,04	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,04

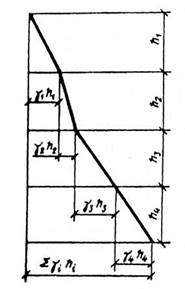
В естественных условиях кроме напряжений от внешней нагрузки, прикладываемой к основанию, в каждой конкретной точке основания действуют напряжения от собственного веса лежащих выше слоев грунта. Эпюра этих напряжений по глубине однородного грунта имеет вид треугольника. Эпюра вертикальных напряжений от действия собственного веса грунтов неоднородного состава является ломаной линией (рис. 1.15). Вертикальное напряжение в любой точке основания находят по формуле

,  (1.24) где  - число слоев грунта, от веса которых определяется напряжение;  - удельный вес  - го слоя грунта;  - толщина -го слоя грунта.

Удельный вес водопроницаемого слоя грунта, находящегося ниже уровня подземных вод, определяют с учетом взвешивающего действия воды по выражению (1.6). Если в толще основания имеется водонепроницаемый грунт (глина или суглинок в твердом состоянии), то необходимо учитывать давление столба воды на его кровлю.

Рис. 1.15. Вертикальные напряжения от действия собственного веса грунтов

Для нагрузки, распределенной по закону трапеции, напряжения в грунте определяются суммированием соответствующих напряжений от треугольной и прямоугольной составляющих.

§ 4. Определение напряжений в грунтах

Пример 1.1. Определить напряжение в точке М от сосредоточенной силы N = 15 кН, приложенной к поверхности грунтового основания. Точка М находится на глубине z = 2 м, расстояние от оси силы  r = 4 м  (рис. 1.18).

Решение.  Определяем отношение . По табл. 1.8 для отношения  находим значение коэффициента  и по формуле