Распределение по глубине
вертикальных составляющих напряжений ![]() в
любой точке массива грунта от действия равномерно распределенной нагрузки в
пределах или за пределами плит нагружения может быть определено по методу
угловых точек по формуле
в
любой точке массива грунта от действия равномерно распределенной нагрузки в
пределах или за пределами плит нагружения может быть определено по методу
угловых точек по формуле
![]() , где Кс – коэффициент, определяемый в
зависимости от отношения сторон прямоугольной площади загружения
, где Кс – коэффициент, определяемый в
зависимости от отношения сторон прямоугольной площади загружения ![]() (
(![]() –
большая сторона,
–
большая сторона, ![]() –
меньшая сторона) и отношения
–
меньшая сторона) и отношения ![]() (z – глубина, на которой
определяется напряжение
(z – глубина, на которой
определяется напряжение ![]() );
); ![]() –
интенсивность равномерно распределенной нагрузки, кН.
–
интенсивность равномерно распределенной нагрузки, кН.
В соответствии с этим
заданные площади нагружения разбивают на прямоугольники таким образом, чтобы
они имели общую угловую точку, через которую проходит расчетная вертикаль ![]() .
Для каждого из этих прямоугольников со сторонами
.
Для каждого из этих прямоугольников со сторонами ![]() с
помощью таблиц определяют значения коэффициента
с
помощью таблиц определяют значения коэффициента ![]() и,
пользуясь принципом независимости действия сил, находят алгебраическим
суммированием напряжения в заданных точках массива грунта. Значения
коэффициента
и,
пользуясь принципом независимости действия сил, находят алгебраическим
суммированием напряжения в заданных точках массива грунта. Значения
коэффициента ![]() и примеры
расчета приведены в /7, с. 88, 9/.
и примеры
расчета приведены в /7, с. 88, 9/.
Задание 4
Для случая действия на поверхности массива грунта нагрузки, распределенной в пределах гибкой полосы по трапецеидальной эпюре, значение вертикального сжимающего напряжения в заданной точке массива грунта определяют путем суммирования напряжений от прямоугольного и треугольного элементов эпюры внешней нагрузки.
Вертикальные напряжения ![]() ,
возникающие от действия полосообразной равномерно распределенной нагрузки
(прямоугольный элемент эпюры внешней нагрузки), определяют по формуле
,
возникающие от действия полосообразной равномерно распределенной нагрузки
(прямоугольный элемент эпюры внешней нагрузки), определяют по формуле
![]() , где Кz – коэффициент, определяемый в зависимости от
значения относительных координат
, где Кz – коэффициент, определяемый в зависимости от
значения относительных координат ![]() и
и ![]() /7,
с. 95/; Р – вертикальная равномерно распределенная нагрузка, кН.
/7,
с. 95/; Р – вертикальная равномерно распределенная нагрузка, кН.
Вертикальные напряжения ![]() ,
возникающие от действия полосообразной неравномерной нагрузки, распределенной
по закону треугольника (треугольный элемент эпюры внешней нагрузки),
определяются по формуле
,
возникающие от действия полосообразной неравномерной нагрузки, распределенной
по закону треугольника (треугольный элемент эпюры внешней нагрузки),
определяются по формуле
![]() , где
, где ![]() –
коэффициент, определяемый в зависимости от значения относительных координат
–
коэффициент, определяемый в зависимости от значения относительных координат ![]() и
и ![]() /7,
с. 99/; Р – наибольшая ордината треугольной нагрузки, кН. Примеры
расчета приведены в /7,9/.
/7,
с. 99/; Р – наибольшая ордината треугольной нагрузки, кН. Примеры
расчета приведены в /7,9/.
Задание 5
В проектной практике широко
распространен расчет устойчивости откоса по методу круглоцилиндрических
поверхностей скольжения. Проверка устойчивости откоса сводится к построениям по
рисунку 8. За коэффициент устойчивости откоса ![]() принимают
отношение момента сил Муд, удерживающих откос от сдвига, к
моменту сил Мсдв, стремящихся сдвинуть откос:
принимают
отношение момента сил Муд, удерживающих откос от сдвига, к
моменту сил Мсдв, стремящихся сдвинуть откос:
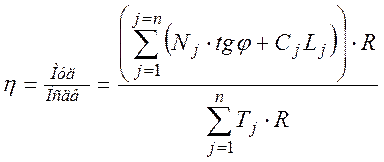 , где
, где ![]() –
число отсеков, на которые делится призма скольжения;
–
число отсеков, на которые делится призма скольжения; ![]() –
нормальные составляющие от веса отсеков
–
нормальные составляющие от веса отсеков ![]() , кН.
Здесь
, кН.
Здесь ![]() -
вес расчетного отсека, кН;
-
вес расчетного отсека, кН; ![]() –
угол между направлением силы
–
угол между направлением силы ![]() и
нормальной составляющей
и
нормальной составляющей ![]() ,
град;
,
град; ![]() –
угол внутреннего трения, град;
–
угол внутреннего трения, град; ![]() –
удельное оцепление, кПа;
–
удельное оцепление, кПа; ![]() –
длина дуги скольжения, м; R – радиус круглоцилиндрической дуги скольжения, м;
–
длина дуги скольжения, м; R – радиус круглоцилиндрической дуги скольжения, м; ![]() -
касательные составляющие от веса отсеков
-
касательные составляющие от веса отсеков ![]() , кН.
, кН.
Для откоса в однородной толще грунтов при определении ординат центра наиболее опасной круглоцилиндрической поверхности скольжения можно пользоваться графиком Янбу /6, 9/.
При расчете ![]() значение
момента принимается отрицательным для восходящей ветви дуги скольжения и положительным
для нисходящей.
значение
момента принимается отрицательным для восходящей ветви дуги скольжения и положительным
для нисходящей.
Радиус круглоцилиндрической
дуги скольжения ![]() ,
а также ширину и высоту отсеков допускается определять графически с расчетной
схемы, выполняемой в масштабе. Для расчета выделяют I погонный метр по длине
откоса (перпендикулярно к плоскости чертежа). Вес расчетного отсека
определяется как произведение удельного веса грунта на объем отсека. Примеры
расчета приведены в /6, 9/.
,
а также ширину и высоту отсеков допускается определять графически с расчетной
схемы, выполняемой в масштабе. Для расчета выделяют I погонный метр по длине
откоса (перпендикулярно к плоскости чертежа). Вес расчетного отсека
определяется как произведение удельного веса грунта на объем отсека. Примеры
расчета приведены в /6, 9/.
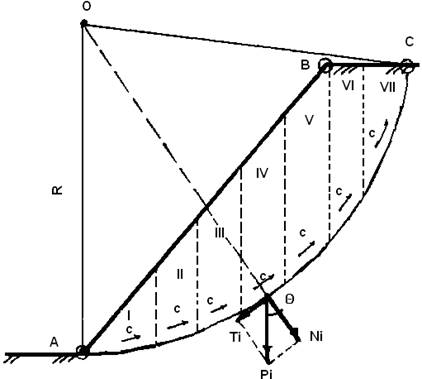
Рисунок 8 - Определение устойчивости откоса методом
круглоциндрических поверхностей скольжения
Задание 6
Определение давления грунта на вертикальную гладкую подпорную стенку с учетом внутреннего трения и сцепления грунта проводится по следующим формулам:
активное давление грунта ![]() ,
кПа, в любой точке стенки
,
кПа, в любой точке стенки
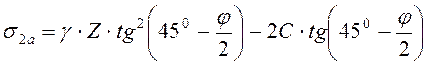 , где
, где ![]() –
расстояние точки от поверхности засыпки, м;
–
расстояние точки от поверхности засыпки, м;
пассивное давление грунта ![]() ,
кПа, в любой точке стенки
,
кПа, в любой точке стенки
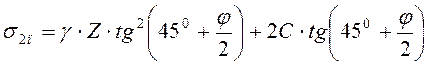 ;
;
равнодействующая ![]() ,
кН/м, активного давления грунта
,
кН/м, активного давления грунта
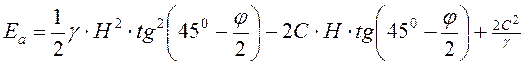
где Н - высота подпорной стенки; равнодействующая ![]() ,
кН/м, пассивного давления грунта
,
кН/м, пассивного давления грунта
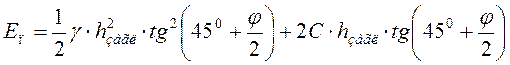 , где
, где ![]() -
заглубление фундамента подпорной стенки, м.
-
заглубление фундамента подпорной стенки, м.
Точка приложения ![]() находится
от подошвы фундамента подпорной стенки на расстоянии
находится
от подошвы фундамента подпорной стенки на расстоянии ![]() , м,
где
, м,
где ![]() –
высота части стенки, м, не воспринимающая давления грунта, определяемая по
формуле
–
высота части стенки, м, не воспринимающая давления грунта, определяемая по
формуле
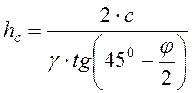 .
.
Точка приложения ![]() находится
на высоте
находится
на высоте ![]() , м,
от подошвы фундамента подпорной стенки.
, м,
от подошвы фундамента подпорной стенки.
![]() , где
, где ![]() –
пассивное давление грунта, кПа, в уровне подошвы фундамента при
–
пассивное давление грунта, кПа, в уровне подошвы фундамента при ![]() ; d – пассивное давление грунта,
кПа, в уровне обреза фундамента при
; d – пассивное давление грунта,
кПа, в уровне обреза фундамента при ![]() .
.
Примеры расчета приведены в /5, 7, 9/.
Для определения давления грунта на подпорную стенку графическим методом можно использовать построения Ш.Кулона.
Последовательность такого определения приведена в /5,7/. Действие сплошной равномерно распределенной пригрузки горизонтальной поверхности засыпки грунта в этом случае заменяется эквивалентной высотой слоя грунта
![]() .
.
Задание 7
Значение полной
стабилизированной осадки грунтовой толщи ![]() по
методу послойного суммирования определяют как сумму осадок элементарных слоев
грунта по формуле
по
методу послойного суммирования определяют как сумму осадок элементарных слоев
грунта по формуле
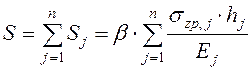 , где
, где ![]() –
среднее значение дополнительного вертикального нормального напряжения, кПа, в
–
среднее значение дополнительного вертикального нормального напряжения, кПа, в ![]() – м
слое грунта, равное полусумме указанных напряжений на верхней
– м
слое грунта, равное полусумме указанных напряжений на верхней ![]() , и
нижней
, и
нижней ![]() границах
слоя по вертикали, проходящей через центр полосообразной нагрузки
границах
слоя по вертикали, проходящей через центр полосообразной нагрузки
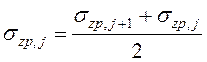 ;
;
![]() –
безразмерный коэффициент;
–
безразмерный коэффициент; ![]() и
и ![]() –
соответственно толщина, м и модуль деформации, кПа,
–
соответственно толщина, м и модуль деформации, кПа, ![]() - го
слоя грунта;
- го
слоя грунта; ![]() – число
слоев, на которое разбита сжимаемая толща основания.
– число
слоев, на которое разбита сжимаемая толща основания.
Напряжение ![]() вычисляются
по формуле
вычисляются
по формуле
![]() ,
,
где ![]() –
коэффициент, принимаемый по /3,7,9/ для полосообразной нагрузки (
–
коэффициент, принимаемый по /3,7,9/ для полосообразной нагрузки (![]() ) в
зависимости от относительной глубины
) в
зависимости от относительной глубины ![]() ;
; ![]() –
дополнительное вертикальное давление на основание. Здесь
–
дополнительное вертикальное давление на основание. Здесь ![]() –
среднее давление под подошвой фундамента, кПа;
–
среднее давление под подошвой фундамента, кПа; ![]() –
вертикальное
–
вертикальное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.