Энергетический и кинематический расчет привода. Проектировочный расчёт конической передачи. Проверочный расчёт зубчатой передачи

коэффициент, учитывающий распределение нагрузки, между зубьями при 8 степени точности и окружной скорости V = 0,061

KHδ = 1,05

KHβ = 1

Проверка контактных напряжений

δH = 470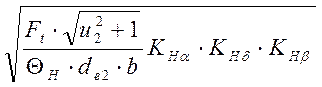 =  644

4 Проектный расчет зубчатой передачи

выбираем материал для шестерни – Сталь 45 (улучшение) HB₁ 285, σ_т1 = 650 МПа колесо – Сталь 45 (улучшение) HB₂ 250, σ_т2 = 540 МПа

HB1 =360

HB2 =325

Определяем коэффициенты долговечности для шестерни и колеса

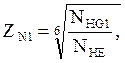                   (6.1)

где:    Z_N1 – коэффициент долговечности для шестерни

N_HG1 = 30·HB₁^2,4

где:    N_HG1 – число циклов перемены напряжений

HB₁ – твёрдость материала шестерни, HB

N_HG1 = 30·360^2,4 = 4.095·10⁷

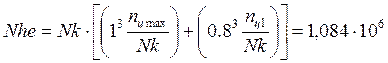
где:    Nk=60·n1·Lh = 8.085·10⁷ – число циклов перемены напряжений

n_цmax = n1·Lh·0.6 = 8.085·10⁵

n_ц1 = n1·0.4·Lh = 5,39*10⁵

 

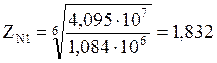
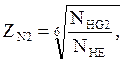                                      (6.2)

где:    Z_N2 – коэффициент долговечности для шестерни

N_HG2 = 30·HB₂^2,4

где:    N_HG2 – число циклов перемены напряжений

HB₂ – твёрдость материала колеса, HB

N_HG2 = 30·325^2,4 = 3,204·10⁷

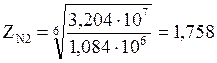
Определяем допускаемые контактные напряжения

где:    [σ]_H1 – допускаемые контактные напряжения на шестерне, МПа

σ_Hlim1 = 2·HB1+70,         σ_Hlim1 = 2·360+70 = 790

где:    σ_Hlim1 – предел контактной выносливости, Мпа

Z_N1 – коэффициент долговечности для шестерни (см формулу 6.1)

Z_R – коэффициент шероховатости

Z_v – коэффициент окружной скорости

S_H – коэффициент запаса прочности

где:    [σ]_H2 – допускаемые контактные напряжения на колесе, МПа

σ_Hlim2 = 2·HB2+70,         σ_Hlim2 = 2·325+70 = 720

где:    σ_Hlim1 – предел контактной выносливости, МПа

Z_N2 – коэффициент долговечности для шестерни (см формулу 6.2)

Z_R – коэффициент шероховатости

Z_v – коэффициент окружной скорости

S_H – коэффициент запаса прочности

где:    [σ]_H – допускаемые контактные напряжения, МПа

[σ]_H1 – допускаемые контактные напряжения на шестерне, МПа

               [σ]_H2 - допускаемые контактные напряжения на колесе, МПа

условие выполняется следовательно в дальнейших расчётах будем учитывать допускаемые контактные напряжения [σ]_H

Определяем допускаемые напряжения изгиба

где:    [σ]_F1 – допускаемые напряжения изгиба для шестерни, МПа

σ_Flim1 =1,75·HB1,  σ_Flim1 = 1,75·360=630

где:    σ_Flim1 – предел выносливости, Мпа

       

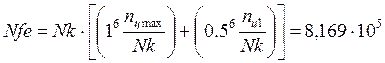
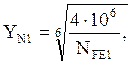
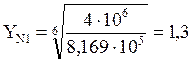
где:    Y_N1 – коэффициент долговечности

Y_R – коэффициент влияния шероховатости 

Y_a – коэффициент влияния двустороннего приложения нагрузки

S_F – коэффициент запаса прочности

где:    [σ]_F2 – допускаемые напряжения изгиба для колеса, МПа

σ_Flim2 =1,75·HB2,  σ_Flim2 = 1,75·325=568,75

где:    σ_Flim2 – предел выносливости, МПа

      

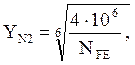
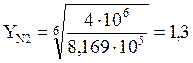
где:    Y_N2 – коэффициент долговечности           

Y_R – коэффициент влияния шероховатости

Y_a – коэффициент влияния двустороннего приложения нагрузки

S_F – коэффициент запаса прочности

для дальнейших расчётов принимаем минимальное из допускаемых напряжений изгиба т.е. [σ]_F = [σ]_F2 = 436

Определяем межосевое расстояние

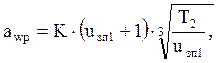
где:    a_wp – предварительное межосевое расстояние, мм

K – коэффициент поверхностной твердости К=10

где:    v – окружная скорость, м/с

a_wp – предварительное межосевое расстояние, мм

 

назначаем 9 степеней точности табл 2.5 исходя из полученной скорости v

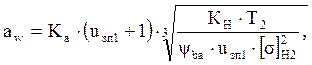
где:    a_w – межосевое расстояние, мм   

К_а – коэффициент передачи

   для косозубых и шевронных колес

ψ_ba – коэффициент ширины колеса

принимаем коэффициент ширины- при несимметричном расположении колёс относительно опор

K_H = K_hb·K_hv·K_ha, где:    K_hb = 1+(K_hbo-1)·K_hw,    

где:     K_hbo – коэффициент неравномерности распределения нагрузки в начальный период работы передачи

K_hw – коэффициент приработки зубьев

   

K_hb = 1+(1,18-1)0,26=1,047-коэффициент динамики нагружения

коэфф неравномерности распределения нагрузки по длине контактных линий

К_ha = 1+(K_hao-1)·K_hw,                                   где:    K_hao =1+А·(n_ст-5),          где: К_hao -  коэффициент неравномерности распределения нагрузки в  начальный период         работы передачи              

n_ст – степень точности передачи (принимаем n_ст =7 исходя из  выполнения          дальнейшего условия)

A=0.25 – коэфф.

K_hao = 1+0,25·(7-5) = 1,5 (<1,6)        

K_ha = 1+(1,5-1)·0,26= 1,13                

K_H = 1,047        

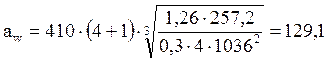
принимаем межосевое расстояние по ГОСТ 6636-69 a_w = 130, округлив до ближайшего стандартного

Предварительные параметры передачи

где:    d₂ – делительный диаметр колеса, мм

a_w – межосевое расстояние, мм

b₂ = ψ_ba·a_w, где:    b₂ – ширина колеса, мм

ψ_ba – коэффициент ширины колеса

b₂ = 0,3·130=39

округлим до ближайшего стандартного числа, принимаем b₂ = 39м

где:      m_max – максимальное значение модуля передачи, мм

где:    m_min – минимальное значение модуля передачи, мм

K_F = K_fv·K_fb·K_hao, где:    K_fv – коэффициент динамики нагружения         

   

K_fb = 0,18+0,82·K_hbo, где:    К_fb – коэффициент неравномерности распределения нагрузки

К_fb = 0,18+0,82·1,18=1,148

К_F = 1,11·1,148·1,5 = 1,91

Принимаем по ГОСТ 9563-60 m =3 мм по стандартному ряду

Определяем суммарное число зубьев и угол наклона

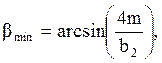
где:    β_min – минимальный угол наклона зубьев, ˚

где:    z_s  - суммарное число зубьев

округляем в меньшую строну до ближайшего целого, принимаем z_s = 83

где:    β – угол наклона зубьев колеса, ˚

округляем по ряду предпочтительных чисел, принимаем β=18 ˚

где:    z₁ – число зубьев шестерни

   

z₁ колеса делаем без смещения, принимаем x₁=0, x₂=0

где:    z₂ – число зубьев колеса

z₂ = 16*4=64

фактическое передаточное число

где:    u_фзп – фактическое передаточное число зубчатой передачи

Размеры колёс

          

где     d₁ – делительный диаметр шестерни, мм принимаем d₁ = 51мм

d₂ = m·z2 ,  d₂ = 192

где:    d₂ – делительный диаметр колеса, мм

y=-3,33  -коэффициент воспринимаемого смещения           

x1=0

x2=0

 

d_a1 = 76,5

где:    d_a1 – диаметр вершин зубьев шестерни, мм

d_f1 =43                   где:    d_f1 – диаметр впадин зубьев шестерни, мм

d_a2 = 218

где:    d_a2 – диаметр вершин зубьев колеса, мм

где: d_f2 – диаметр впадин зубьев колеса, мм                                             

d_f2 =  184,5

5 Проверочный расчёт зубчатой передачи

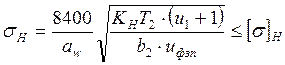
где:    σ_H  - расчётные контактные напряжения, МПа

условие выполняется т.е. передача по условию контактной прочности является работоспособной.

Силы в зацеплении

F_t=2·10³·T2/d₁,     F_t = 2,655·10³

где:    F_t – окружная сила, Н

F_r = F_t·0,364/cosβ, F_r = 1,016*10³

где:    F_r – радиальная сила, Н

F_a = F_t·cosβ, F_a = 2,525*10³

Проверка зубьев по напряжениям изгиба

; где:    σ_F2 – расчётное напряжение изгиба, МПа

[σ]_F2 – допускаемые напряжения изгиба, МПа

- приведенное число зубьев

Y_FS2 – коэффициент формы зуба,

– коэффициент угла наклона зубьев

Y_e – коэффициент перекрытия зубьев,

<436

Условие выполняется, т.е. зубья выдержат напряжения изгиба.

; где:    σ_F2 – расчётное напряжение изгиба, МПа

 - приведенное число зубьев

Y_FS1 – коэффициент формы зуба шестерни

         

Условие выполняется, т.е. зубья выдержат напряжения изгиба.

Проверим напряжение изгиба зубьев

KFx = 1

N = 0,25

KFU = 1,04

ZV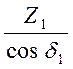1 =  =  9.1

ZV2 = 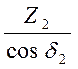 =  467

допустимое напряжение на изгиб

σF1 = 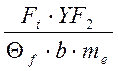·KFα·KFv·KFβ = 1100 МПа

6 Предварительный расчёт валов

Вал 1

 - принимаем исходя из конструктивных размеров муфты

d_п = d+2t= 17+2·3 =23  мм – диаметр под подшипник                                                 где:    t – высота заплечика

t =3

предварительно выбираем подшипник шариковый радиальный однорядный средней серии диаметров       внутреннего кольца 25

d_бп = d_п + 3r = 25+3·1,5 = 29.5 мм – диаметр буртика где:    r = 1,5 – фаска подшипника

f =1,5       

Вал 2

 

 

Принимаем стандартное значение  d₃ = 28 мм

d_п = d₃ + 2·t = 28+2·3=34мм – диаметр вала под подшипник где:    t – высота заплечика

t =3

предварительно выбираем подшипник шариковый радиальный однорядный средней серии с диаметром внутреннего кольца 35

d_{п =}35

d_к = d_п+3r = 35+3·1,5 = 39,5 мм – диаметр под колесо