Срок службы приводного устройства. Выбор двигателя. Кинематический расчет привода. Кинематические и силовые параметры привода

Определяем допускаемое контактное напряжение [σ]_H, Н/мм²:

для шестерни:

[σ]_H1 = К_HL1∙ [σ]_HО1 = 1∙580.9 = 580.9;

для колеса:

[σ]_H2 = К_HL2∙ [σ]_HО2 = 1 ∙514.3 = 514.3.

Так как НВ_1ср = 285.5 ‹ 350 НВ и НВ_2ср = 248.5 ‹ 350 НВ, то косозубая передача рассчитывается на прочность по среднему допускаемому контактному напряжению, Н/мм²:

 [σ]_H = 0.45∙([σ]_H1 + [σ]_H2);

[σ]_H = 0.45∙(580.9 + 514.3) = 492.8.

3.2.1    Определение допускаемых напряжений изгиба для зубьев шестерни [σ]_F1 и колеса [σ]_F2.

a)  Рассчитываем коэффициент долговечности К_HL

Наработка за весь срок службы: для шестерни N₂ = 193.73∙10⁶ циклов, для колеса N₁ = 777.92∙10⁶ циклов.

Число циклов перемены напряжений, соответствующее пределу выносливости, N_FO = 4∙10⁶ для обоих колес.

Так как N₁ › N_FO1 и N₂ › N_FO2, то коэффициент долговечности К_HL1 = 1 и К_HL2 = 1.

b)  По таблице 3.1 / 1, с. 49 / определяем допускаемое напряжение изгиба [σ]_FO в Н/мм², соответствующее числу циклов перемены напряжений N_FO:

для шестерни:

[σ]_FО1 = 1.03 НВ_1ср;

[σ]_FО1 = 1.03∙285.5 = 294.

для колеса:

[σ]_FО2 = 1.03 НВ_2ср;

[σ]_FО2 = 1.03∙248.5 = 256.

с)  Определяем допускаемое напряжение изгиба [σ]_F, Н/мм²:

для шестерни:

[σ]_F1 = К_HL1∙[σ]_FО1 = 1∙294 = 294;

для колеса:

[σ]_F2 = К_HL2∙[σ]_FО2 = 1∙256 = 256.

3.2.3.   Результаты расчетов сводим в таблицу 2.

Таблица 2 – Механические характеристики материалов зубчатой передачи

Элемент передачи	Марка стали	Dпред	Термообработка	НВ1ср	[σ]Н	[σ]F
		Sпред		НВ2ср	Н/мм2
Шестерня	40ХН	125	Улучшение	285.5	580.9	294
Колесо	40ХН	125	Улучшение	248.5	514.3	256

3.3       Проектный расчет на контактную выносливость.

3.3.1    Определяем межосевое расстояние а_w, мм:

а_w ≥ К_а(u + 1) 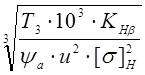, где К_а – вспомогательный коэффициент;

ψ – коэффициент ширины венца колеса;

u – передаточное число редуктора (см. таб.1);

Т₃ – вращающий момент на тихоходном валу редуктора, Н∙м (см. таб.1);

[σ] – допускаемое среднее контактное напряжение (см. 3.2.1, п.с);

К_Нβ – коэффициент неравномерности нагрузки по длине зуба.

а_w ≥ .

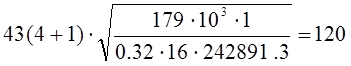3.3.2    Определяем модуль зацепления m, мм:

m = (0.01…0.02) а_w = 1.5.

3.3.3    Определяем угол наклона зубьев β_min для косозубых передач, град:

β_min = arcsin , где b₂ – ширина венца, мм.

β_min = arcsin.

3.3.4  Определяем суммарное число зубьев шестерни и колеса:

z_∑ = z₁ + z₂ = 2a_w∙cos β_min/m;

z_∑ = .

3.3.5  Уточняем действительную величину угла наклона зубьев для косозубых передач, град:

β = arccos z_∑m/(2a_w);

β = .

3.3.6    Определяем число зубьев шестерни:

z₁ = ;

z₁ = .

3.3.7    Определяем число зубьев колеса:

z₂ = z_∑ - z₁;

z₂ = 158 – 32 = 126/

3.3.8  Определяем фактическое передаточное число u_ф и проверяем его отклонение Δu от заданного u:

u _ф = z₂/ z₁;

Δu = ;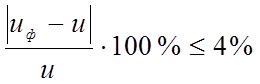

u _ф = 126/32 = 3,94;

Δu = .

3.3.9  Определяем фактическое межосевое расстояние, мм:

a_w = (z₂ + z₂)m/(2cos³β);

a_w = .

3.3.10  Определяем основные геометрические параметры передачи, мм

Параметр	Шестерня	Колесо
Диаметр делительный	d1 = mz1/cosβ d1 = 1.5∙32/0.99 = 48.5	d2 = mz2/cosβ d2 = 1.5∙126/0.99 = 191
Диаметр вершин зубьев	dа1 = d1 + 2m da1 = 48.5 + 2∙1.5 = 51.5	da1 = d2 + 2m da1 = 191 + 2∙1.5 = 194
Диаметр вершин впадин	df1 = d1 – 2.4m df1 = 48.5 – 2.4∙1.5 =45	df2 = d2 – 2.4m df2 = 194 – 2.4∙1.5 = 187.4
Ширина венца	b1 = b2 + (2…4) b1 = 38 + 4 = 42	b2 = ψ∙aw b2 = 0.32∙120 = 38

3.4       Проверочный расчет

3.4.1    Проверяем межосевое расстояние, мм:

a_w = (d₁ + d₂)/2;

a_w =

3.4.2    Проверяем пригодность заготовок колес (см. таб.2):

Условие пригодности заготовок колес:

D_заг  D_пред;            S_заг  S_пред.

Диаметр заготовки шестерни:

D_заг = d_a1 + 6 мм;

D_заг = 51.5 + 6 = 57.5.

Размер заготовки колеса закрытой передачи:

S_заг = b₂ + 4 мм;

S_заг = 38 + 4 = 42.

3.4.3    Проверяем контактные напряжения σ_Н, Н/мм²:

,

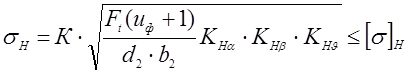где К – вспомогательный коэффициент;

F_t – окружная сила в зацеплении, Н;

К_Нα – коэффициент, учитывающий распределение нагрузки между зубьями, определяется по графику / 1, с63 /;

К_Нβ – коэффициент неравномерности нагрузки по длине зуба;

К_Нυ – коэффициент динамической нагрузки, (см. таб.4.3) / 1, с62 /;

[σ]_Н – допускаемое контактное напряжение, Н/мм².

.

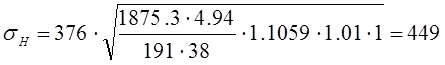Допускаемая недогрузка передачи (σ_Н ‹ [σ]_H) не более 10%

3.4.4    Проверяем напряжения изгиба зубьев шестерни σ_F1 и колеса σ_F1, н/мм²:

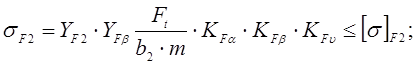
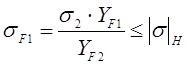, где m – модуль зацепления, мм;

b₂ – ширина зубчатого венца колеса, мм;

K_Hα – коэффициент, учитывающий распределение нагрузки между зубьями (см. п.14) / 1, с63 /;

К_Нυ – коэффициент динамической нагрузки (см. таб.4.3) / 1, с. 62 /;

Y_F1 и Y_F2 – коэффициенты формы зуба шестерни и колеса (см. таб.4.4)

/ 1, с. 64 /;

Y_β – коэффициент, учитывающий наклон зуба;

[σ]_F1 и [σ]_F2 – допускаемые напряжения изгиба шестерни и колеса, Н/мм² (см. таб.2).

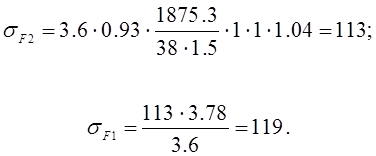
При проверочном расчете σ_F значительно меньше [σ]_F, это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью.

3.4.5.   Результаты расчетов сводим в таблицу 3.

Таблица 3 – Параметры зубчатой цилиндрической передачи, мм

Проектный расчет
Параметр	Значение		Параметр		Значение
Межосевое расстояние аw	120		Угол наклона β		9
Модуль зацепления m	1.5		Диаметр делительной окружности: шестерни d1 колеса d2		48.5 191
Ширина зубьев венца: шестерни b1 колеса b2	42 38		Диаметр окружности вершин: шестерни da1 колеса da2		51,5 194
Число зубьев: шестерни z1 колеса z2	32 126		Диаметр окружности впадин: шестерни df1 колеса df2		45 187.3
Проверочный расчет
Параметр		Допускаемые значения		Расчетные значения	Примечание
Контактные напряжения σН, Н/мм2		492,84		449	9%
Напряжения изгиба, Н/мм2 σF1 σF2		294 256		119 113	55% 60%

4          Расчет открытой передачи

4.1       Проектный расчет

4.1.1    Определяем диаметр ведущего шкива d₁, мм:

d₁ = (52…64), где Т – вращающий момент на быстроходном валу.

d₁ = .

4.1.2    Определяем диаметр ведомого шкива d₂, мм:

d₂ = u∙d₁ (1-ε), где u – передаточное число открытой передачи (см. таб.1);

ε – коэффициент скольжения.

d₂ = 3.25∙140 (1-0.01) = 450.

4.1.3    Определяем фактическое передаточное число u_ф  и проверяем его отклонение Δu от заданного:

u_ф =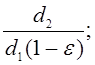

Δu = ;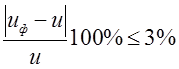

u_ф =;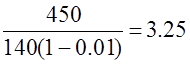

Δu = %.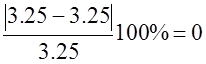

4.1.4    Определяем ориентировочное межосевое расстояние а, мм:

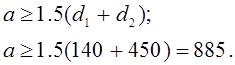
4.1.5    Определяем расчетную длину ремня l, мм:

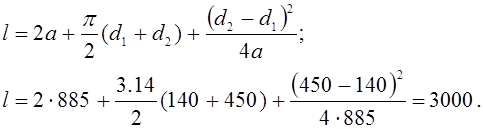
4.1.6    Уточняем значение межосевого расстояния а, мм по стандартной длине l:

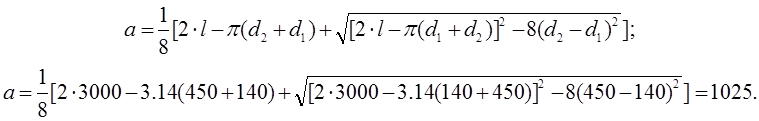4.1.7    Определяем угол обхвата ремнем ведущего шкива α₁, град:

α₁ = 180^о – 57^о(d₂ - d₁)/а;

α₁ = 180^о – 57^о(450-140)/1025 = 163.

Угол α₁ должен быть  150^о.

4.1.8    Определяем скорость ремня υ, м/с:

υ =

где d₁ – диаметр ведущего шкива;

n₁ – частота вращения ведущего шкива (см. таб.1);

[υ] = 35 м/с – допускаемая скорость.

υ =

4.1.9    Определяем частоту пробегов ремня U, с^-1:

U = l/υ [U], где l – стандартная длина ремня, м;

[U] = 15 с^-1 – допускаемая частота пробега.

U = .

4.1.10  Определяем окружную силу F_t, Н, передаваемую ремнем:

F_t = P_ном ∙ 10³/υ, где P_ном – номинальная мощность двигателя, кВт (см. таб.1);

υ – скорость ремня, м/с.

F_t =

4.1.11  Определяем допускаемую удельную окружную силу [k], н/мм²:

[k] = [k_о]∙С_θ∙С_α∙С_υ∙С_p∙С_d∙С_F, где [k_о] – допускаемая приведенная удельная окружная сила, н/мм²

С – поправочные коэффициенты (см. таб.5.2) / 1, с78-80 /.

[k] = 1.25∙1∙0.94∙1.03∙0.9∙0.85∙1.2 = 1.11.

4.1.12  Определяем ширину ремня b, мм:

b = F_t / δ[k_п];

b =

4.1.13  Определяем площадь поперечного сечения ремня А, мм²:

А = δ∙b;

A = 2.8∙71 = 198.8.

4.1.14  Определяем силу предварительного напряжения ремня F_o, Н:

F_o = А∙σ_о, где σ_о – предварительное напряжение, Н/мм².

F_o = 198,8∙2 = 397.6.

4.1.15  Определяем силы напряжения ведущей F₁ и ведомой F₂ ветвей ремня, Н:

F₁ = F_o + F_t/2;                   F₂ = F_o – F_t/2;

F₁ =

F₂ =

4.1.16  Определяем силу давления на вал F_oп, Н:

F_oп = 2 F_o sin (α₁/2);

F_oп = 2∙397.6∙sin (163/2) = 787.

4.2       Проверочный расчет

4.2.1    Проверяем прочность ремня по максимальным напряжениям в сечении ведущей ветви σ_max, Н/мм²:

σ_max = σ₁ + σ_и + σ_υ[ σ]_p, где σ₁ – напряжения растяжения, Н/мм²;

σ_и – напряжения изгиба, Н/мм²;

σ_υ – напряжения от центробежных сил, Н/мм²;

σ_р – допускаемое напряжение растяжения, Н/мм².

σ₁= ;

σ_и =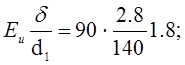

где Е_и – модуль продольной упругости при изгибе для прорезиненных ремней.

σ_υ = ;

σ_р = 8;

σ_max = 2.54 + 1.8 + 0.029 = 4.369.

4.2.2    Результаты расчетов сводим в таблицу 4.

Таблица 4 – Параметры плоскоременной передачи, мм

Параметр	Значение	Параметр	Значение
Тип ремня	плоский	Число пробегов ремня U, 1/с	0.58
Межосевое расстояние а	1025	Диаметр ведущего шкива d1	140
Толщина ремня δ	2.8	Диаметр ведомого шкива d2	450
Ширина ремня b	71	Максимальное напряжение σmax, Н/мм2	4.4
Длина ремня l	3000	Начальное напряжение Fo, Н	397.6
Угол обхвата α1	163	Сила давления ремня на вал Foп, Н	787

5          Выбор муфты

В проектных приводах применимы компенсирующие разъемные муфты нерасцепляемого класса в стандартном исполнении.

Для соединения выходных концов тихоходного вала редуктора и привода