





Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Автоматики и Вычислительной техники
ОТЧЕТ
Расчётное задание 1
11 вариант
Выполнил: студент гр. 2081/3
Проверил:
----
/подпись преподавателя, дата/
Санкт-Петербург
2009г.
Часть 1.
Партия из N тензорезисторов подвергается выборочному контролю с разрушением. Партия бракуется, если из m наудачу выбранных тензорезисторов хотя бы один не удовлетворяет требованиям технических условий. Какова вероятность забраковать партию тензорезисторов, если она содержит k% дефектных.
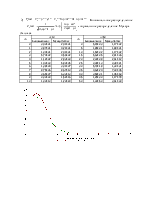
Решить задачу сначала точно. Затем аппроксимировать процедуру выбора тензорезисторов а) биномиальным распределением и б) распределением Пуассона и получить приближенное решение. Сравнить точные и приближенные ответы и объяснить различие.
Дано:
N = 100
m = 12
k = 11
Решение:
h = k*N = 11%*100 = 11 – количество дефектных деталей
Пусть есть множество из N элементов. Случайным образом
выбирается m элементов. Партия считается нормальной, если нет
бракованных деталей, т.е. b=0. Вероятность выбора нормальных деталей будет равна ![]() . Вероятность забраковать партию
. Вероятность забраковать партию
![]() .
.
а) Аппроксимация по
биномиальному распределению будет иметь вид ![]() .
Вероятность забраковать
.
Вероятность забраковать ![]() .
.
б) Аппроксимация по
Пуассону будет равна ![]() . Вероятность
забраковать
. Вероятность
забраковать ![]() .
.
Вывод:
Вероятности забраковать партию, вычисленные с помощью биномиального распределения и распределения Пуассона, отличаются от точного. Это отличие можно объяснить тем, что биноминальное распределение и распределение Пуассона – это аппроксимирующие функции, которые используются при больших N и малых m.
Часть 2
Передаче по каналу связи с равной вероятностью подлежат кодовые слова x1, x2, x3, x4. Канал симметричный, вероятность искажения каждого отдельного символа равна q. В результате однократной передачи на приемной стороне принято слово y1. В результате повторной передачи того же слова на приемной стороне принято слово y2. В результате последней (третьей) передачи того же слова на приемной стороне принято слово y3.
Для исходного ансамбля (x1,x2,x3,x4) рассчитать:
1. энтропию ансамбля возможных сообщений.
2. апостериорное распределение вероятностей передачи каждого из исходных кодовых слов после получения слов y1, y2, y3.
3. количество информации в полученных сообщениях после передачи слов y1, y2, y3
Рассмотреть три передачи как одну передачу слова утроенной длины (кодовые слова X1 = x1x1x1, X2 = x2x2x2, X3 = x3x3x3, X4 = x4x4x4, на выходе Y = y1y2y3). Рассчитать
1. энтропию ансамбля возможных сообщений.
2. апостериорное распределение вероятностей передачи после получения слова Y.
3. количество информации в полученном сообщении после передачи слова Y.
Графически представить априорные и апостериорные распределения возможных сообщений (на одном графике) для первого и второго случая. Проанализировать результаты с точки зрения здравого смысла.
Дано:
q = 0,25
x1 = 100000 y1 = 010111
x2 = 001011 y2 = 010111
x3 = 010101 y3 = 110111
x4 = 011110
Решение:
Вероятности
передачи каждого сообщения одинаковы: ![]() .
.
Априорная энтропия: ![]()
Апостериорная энтропия после
получения y1: ![]()
![]()
![]()
![]()
![]()
Полная
вероятность ![]() 1/4* (pq5+p3q3+p5q+p4q2)=
1/4* (pq5+p3q3+p5q+p4q2)=
=1/4* (0.00073242 + 0.0065918 + 0.059326 + 0.019775) = 0.0172
Апостериорная
вероятность передачи сообщения после получения y1 по формуле Байеса: ![]() .
.
![]() 0.8617
0.8617
![]() 0.0957
0.0957
![]() 0.0106
0.0106
![]() 0.0319
0.0319
![]() = 0.7374
= 0.7374
![]() 2 – 0.7374= 1.2626– количество информации, полученное
после передачи сообщения y1.
2 – 0.7374= 1.2626– количество информации, полученное
после передачи сообщения y1.
Апостериорная энтропия после
получения y2: ![]()
![]()
![]()
![]()
![]()
Полная
вероятность ![]() 1/4* (pq5+p3q3+p5q+p4q2)=
1/4* (pq5+p3q3+p5q+p4q2)=
=1/4* (0.00073242 + 0.0065918 + 0.059326 + 0.019775) = 0.0172
Апостериорная
вероятность передачи сообщения после получения y2 по формуле Байеса: ![]() .
.
![]() 0.8617
0.8617
![]() 0.0957
0.0957
![]() 0.0106
0.0106
![]() 0.0319
0.0319
![]() = 0.7374
= 0.7374
![]() 1.2626 – 0.7374= 0.5252– количество информации,
полученное после передачи сообщения y2.
1.2626 – 0.7374= 0.5252– количество информации,
полученное после передачи сообщения y2.
Апостериорная энтропия после получения y3: ![]()
![]()
![]()
![]()
![]()
Полная
вероятность ![]() 1/4* (p2q4+p2q4+p4q2+p3q3)=
1/4* (p2q4+p2q4+p4q2+p3q3)=
=1/4* (0.0021973 + 0.0021973 + 0.019775 + 0.0065918) = 0.0076904
Апостериорная
вероятность передачи сообщения после получения y3 по формуле Байеса: ![]() .
.
![]() 0.07143
0.07143
![]() 0.07143
0.07143
![]() 0.64285
0.64285
![]() 0.21429
0.21429
![]() = 1.43
= 1.43
![]() 0.5252 – 1.43 = -0.9048 – количество информации,
полученное после передачи сообщения y3.
0.5252 – 1.43 = -0.9048 – количество информации,
полученное после передачи сообщения y3.
Передача слова утроенной длины:
Вероятности
передачи каждого сообщения одинаковы: ![]() .
.
Априорная энтропия: ![]()
Апостериорная энтропия
после получения Y: ![]()
![]()
![]()
![]()
![]()
Полная
вероятность ![]() 1/4* (p4q14+p8q10+p14q4+p11q7)=
1/4* (p4q14+p8q10+p14q4+p11q7)=
=1/4* (1.1787e-009 + 9.5475e-008 + 6.9601e-005 + 2.5778e-006) = 0.000018
Апостериорная
вероятность передачи сообщения после получения Y
по формуле Байеса: ![]() .
.
![]() 0.0000163
0.0000163
![]() 0.001321
0.001321
![]() 0.963
0.963
![]() 0.035666
0.035666
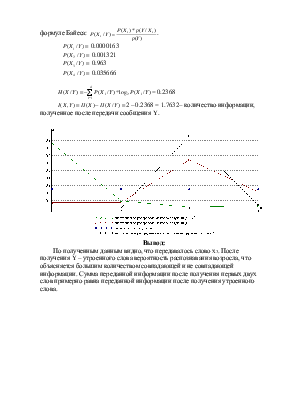
![]() = 0.2368
= 0.2368
![]() 2 – 0.2368 = 1.7632– количество информации, полученное
после передачи сообщения
2 – 0.2368 = 1.7632– количество информации, полученное
после передачи сообщения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.