Таким образом наша гипотеза по данному критерию не подтвердилась.
б) По критерию «омега-квадрат» Мизеса:
Статистика критерия - 0.000167, Критическое значение критерия - 0.461400
0.000167 < 0.461400
Наша гипотеза подтвердилась по критерию «омега-квадрат» Мизеса.
в) По критерию «хи-квадрат»:
Статистика критерия - 36.387717,
Критическое значение критерия - 59.303512
36.387717 > 59.303512
Наша гипотеза подтвердилась по критерию «хи-квадрат»
Вывод: Выборка была получена из биномиального отрицательного распределения.
Данное предположение проверено с помощью трех критериев: «хи-квадрат», Колмогорова-Смирнова, «омега-квадрат», правильность гипотезы подтверждают два из них – по критерию «омега-квадрат» Мизеса и по критерию «хи-квадрат»,
При исследовании других гипотез значения критерия получались существенно превышающими критические значения, следовательно можно сделать вывод, что гипотеза о биномиальном отрицательном распределении вероятнее всего
Часть 2
Оценивание методом наименьших квадратов (МНК) и методом наименьшей дисперсии (МНД) коэффициентов полиномов, аппроксимирующих результаты измерений зависимых переменных.
В результате измерений при значениях независимой переменной
![]()
получены следующие данные:
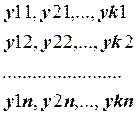
Выборочные значения находятся в файлах mnk_01.dat - mnk_10.dat.
Вычислить:
·
в каждой точке ![]() средние
арифметические значения
средние
арифметические значения ![]() ,
оценки дисперсий
,
оценки дисперсий ![]() ,
параметрические толерантные пределы для погрешностей, доверительные интервалы
для математических ожиданий, проверить гипотезу о равенстве дисперсий в этих
точках по критерию Кочрена;
,
параметрические толерантные пределы для погрешностей, доверительные интервалы
для математических ожиданий, проверить гипотезу о равенстве дисперсий в этих
точках по критерию Кочрена;
· оценки коэффициентов полинома МНК или МНД (в зависимости от исхода проверки гипотез о равенстве дисперсий)
· проверить гипотезу о степени полинома, и если она не будет отвергнута, оценить дисперсии и ковариации оценок коэффициентов,
· вычислить коэффициенты корреляции между оценками коэффициентов.
Внимание! Степень полинома a-priori не известна, поэтому необходимо начинать попытки аппроксимации с наименьшей степени и проверять гипотезу о степени полинома. При отклонении гипотезы увеличить степень аппроксимирующего полинома на единицу и проделать указанную процедуру вновь.
Приводить все промежуточные результаты, получаемые при каждой попытке.
Пусть гипотеза оказалась не отвергнутой при степени q. Тогда следует задать степень полинома равной k-1 и вновь вычислить оценки коэффициентов этого полинома и ковариационную матрицу оценок коэффициентов. Сопоставить с предыдущими результатами и прокомментировать возможное увеличение дисперсий оценок коэффициентов и ухудшение обусловленности задачи.
Представление результатов:
· числовое - результаты, полученные на каждой итерации при каждом значении степени полинома q, в том числе, значения статистики критерия проверки степени полинома и критические значения критерия,
· графическое - изобразить все точки, толерантные пределы и границы доверительных интервалов, средние значения и полученную аппроксимирующую полиномиальную функцию, причем эту функцию, границы доверительных интервалов и толерантные пределы соединить плавной линией; там же нанести функцию, полученную при безизбыточной аппроксимации полиномом степени k-1.
Решение:
Исходные данные
X -4.000000 -3.000000 -2.000000 -1.000000 0.000000 1.000000 2.000000 3.000000 4.000000 5.000000];
y[i][j]=-263.732788 -264.959015 -265.094299 -262.590668 -263.499786 -267.376984 -262.903656 -263.810364 -267.125183 -266.257568 -265.046509 -264.047546 -112.014404 -115.308929 -115.084900 -117.640053 -114.569267 -113.797897 -118.800133 -114.311508 -115.742409 -118.488380 -115.052811 -119.303612 -36.693947 -37.932327 -36.288418 -38.196644 -36.842899 -36.178280 -38.233372 -39.351887 -34.505157 -35.980789 -35.885448 -36.931946 -10.032688 -2.363843 -5.280525 -4.266422 -3.870848 -5.319100 -4.078475 -4.104988 -5.459283 -11.338930 -4.534472 -0.692736 -6.898824 -1.157524 0.921587 -5.522852 2.305175 0.287174 -1.475935 -2.826334 -7.966957 -6.053497 -0.746231 -2.725415 2.034903 9.025040 4.939837 10.702812 6.900819 5.061471 4.858550 8.613982 7.250342 1.434525 8.144498 6.784441 31.812222 33.113670 34.930218 36.428665 39.478394 34.536610 34.872650 31.039917 35.646103 36.803154 29.299805 36.032738 111.515182 106.023239 112.894379 104.392776 113.612106 111.135345 114.423164 110.606712 113.314201 114.643440 110.533257 108.296227 267.989685 265.038422 265.229095 263.136108 258.956421 269.181549 265.292633 266.644775 267.172211 265.241211 266.895355 266.860016 511.054291 503.214752 512.287354 517.409668 501.134888 508.789978 511.562103 502.969543 513.406921 510.716248 508.365417 506.564880
1) Средние арифметические значения y в каждой точке:
<y1> = -220.748233
<y2> = -115.842859
<y3> = -36.918426
<y4> = -5.111859
<y5> = -2.654969
<y6> = 6.312602
<y7> = 34.499512
<y8> = 110.949169
<y9> = 265.636457
<y10> = 508.956337
2) Оценки дисперсий y в каждой точке:
D1 = 23280.569749
D2 = 5.022802
D3 = 1.734885
D4 = 8.630294
D5 = 10.851211
D6 = 7.671806
D7 = 7.814279
D8 = 10.647200
D9 = 6.930471
D10 = 22.975399
3) Параметрические толерантные пределы для погрешностей в каждой точке:
В точке х1 - [ -436.835727, 436.835727 ]
В точке х2 - [ -6.416444, 6.416444 ]
В точке х3 - [ -3.771001, 3.771001 ]
В точке х4 - [ -8.410739, 8.410739 ]
В точке х5 - [ -9.431059, 9.431059 ]
В точке х6 - [ -7.929945, 7.929945 ]
В точке х7 - [ -8.003239, 8.003239 ]
В точке х8 - [ -9.341983, 9.341983 ]
В точке х9 - [ -7.537073, 7.537073 ]
В точке х10 - [ -13.723120, 13.723120 ]
4) Интервальные оценки для математических ожиданий оценки с доверительной вероятностью 0.8:
y1 - [ -280.484141, -161.012324 ]
y2 - [ -116.720287, -114.965430 ]
y3 - [ -37.434099, -36.402754 ]
y4 - [ -6.262001, -3.961717 ]
y5 - [ -3.944637, -1.365302 ]
y6 - [ 5.228207, 7.396997 ]
y7 - [ 33.405094, 35.593930 ]
y8 - [ 109.671682, 112.226656 ]
y9 - [ 264.605786, 266.667128 ]
y10 - [ 507.079743, 510.832930 ]
5)Проверка гипотезы о равенстве дисперсий в точках xi по критерию Кочрена:
Статистика критерия - 0.996478,
Критическое значение критерия - 0.232000
0.996478 > 0.232000
Мы не имеем достаточных оснований, чтобы считать нашу гипотезу справедливой.
6) Оценка ковариационной матрицы:
23280.570 182.937 9.258 -234.652 -202.993 -203.899 -128.717 25.576 110.781 100.196
182.937 5.023 0.317 -1.616 1.019 -0.457 -2.686 0.462 1.103 -2.843
9.258 0.317 1.735 -1.372 -0.833 -1.380 0.589 1.828 0.801 1.802
-234.652 -1.616 -1.372 8.630 4.760 6.131 0.280 -4.679 -1.416 -5.085
-202.993 1.019 -0.833 4.760 10.851 1.537 0.657 0.743 -2.995 -8.691
-203.899 -0.457 -1.380 6.131 1.537 7.672 -0.816 -6.324 -1.945 -1.872
-128.717 -2.686 0.589 0.280 0.657 -0.816 7.814 1.687 -4.642 1.033
25.576 0.462 1.828 -4.679 0.743 -6.324 1.687 10.647 -0.035 -0.510
110.781 1.103 0.801 -1.416 -2.995 -1.945 -4.642 -0.035 6.930 3.007
100.196 -2.843 1.802 -5.085 -8.691 -1.872 1.033 -0.510 3.007 22.975
7) Проверка гипотезы о степени полинома а) Проверка гипотезы о степени полинома p = 0.
Мы не имеем достаточных оснований, чтобы считать нашу гипотезу справедливой.
Статистика критерия - 22114.403851, критическое значение - 8.812300.
22114.403851 > 8.812300
б) Проверка гипотезы о степени полинома p = 1.
Мы не имеем достаточных оснований, чтобы считать нашу гипотезу справедливой.
Статистика критерия - 5843.656229, критическое значение - 6.041044.
5843.656229 > 6.041044
в) Проверка гипотезы о степени полинома p = 2.
Мы не имеем достаточных оснований, чтобы считать нашу гипотезу справедливой.
Статистика критерия - 4387.880483, критическое значение - 4.875872.
4387.880483 > 4.875872
г) Проверка гипотезы о степени полинома p = 3.
Статистика критерия - 2.634761, критическое значение - 4.283866.
2.634761 < 4.283866
У нас нет достаточных оснований для отклонения этой гипотезы.
- Оценки коэффициентов полинома:
4.011078 -0.067895 2.026670 -0.350767
- Ковариационная матрица вектора оценок полинома:
COV(X,Y) = 0.055 -0.014 -0.006 0.001
-0.014 0.013 0.003 -0.002
-0.006 0.003 0.002 -0.000
0.001 -0.002 -0.000 0.000
- Дисперсии оценок:
0.235 0.115 0.039 0.015
- Корреляционная матрица вектора оценок полинома:
1.000 -0.927 -0.984 0.843 -0.927 1.000 0.973 -0.983 -0.984 0.973 1.000 -0.919 0.843 -0.983 -0.919 1.000
- Число обусловленности Х - 79.750167
к) Безизбыточная аппроксимация полиномом степени p = 9.
Оценки коэффициентов полинома:
0.001 -0.006 -0.038 0.194 0.358 -1.813 2.963 4.880 2.429 -2.655
- Ковариационная матрица вектора оценок полинома:
0.904 -0.372 -0.849 0.304 0.226 -0.073 -0.019 0.006 0.000 -0.000
-0.372 0.456 0.597 -0.360 -0.221 0.083 0.024 -0.007 -0.001 0.000
-0.849 0.597 2.190 -0.591 -0.831 0.174 0.095 -0.019 -0.003 0.001
0.304 -0.360 -0.591 0.326 0.229 -0.080 -0.026 0.007 0.001 -0.000
0.226 -0.221 -0.831 0.229 0.336 -0.069 -0.040 0.008 0.001 -0.000
-0.073 0.083 0.174 -0.080 -0.069 0.021 0.008 -0.002 -0.000 0.000
-0.019 0.024 0.095 -0.026 -0.040 0.008 0.005 -0.001 -0.000 0.000
0.006 -0.007 -0.019 0.007 0.008 -0.002 -0.001 0.000 0.000 -0.000
0.000 -0.001 -0.003 0.001 0.001 -0.000 -0.000 0.000 0.000 -0.000
-0.000 0.000 0.001 -0.000 -0.000 0.000 0.000 -0.000 -0.000 0.000
- Дисперсии оценок:
0.951 0.675 1.480 0.571 0.579 0.144 0.069 0.014 0.003 0.000
- Корреляционная матрица вектора оценок полинома:
1.000 -0.930 -0.914 0.925 0.872 -0.916 -0.842 0.891 0.798 -0.843
-0.930 1.000 0.929 -0.995 -0.914 0.979 0.898 -0.955 -0.866 0.914
-0.914 0.929 1.000 -0.957 -0.995 0.980 0.988 -0.990 -0.974 0.986
0.925 -0.995 -0.957 1.000 0.948 -0.994 -0.935 0.979 0.909 -0.949
0.872 -0.914 -0.995 0.948 1.000 -0.976 -0.998 0.992 0.991 -0.997
-0.916 0.979 0.980 -0.994 -0.976 1.000 0.968 -0.995 -0.948 0.976
-0.842 0.898 0.988 -0.935 -0.998 0.968 1.000 -0.988 -0.997 0.998
0.891 -0.955 -0.990 0.979 0.992 -0.995 -0.988 1.000 0.975 -0.993
0.798 -0.866 -0.974 0.909 0.991 -0.948 -0.997 0.975 1.000 -0.994
-0.843 0.914 0.986 -0.949 -0.997 0.976 0.998 -0.993 -0.994 1.000
- Число обусловленностей Х - 4496364.824
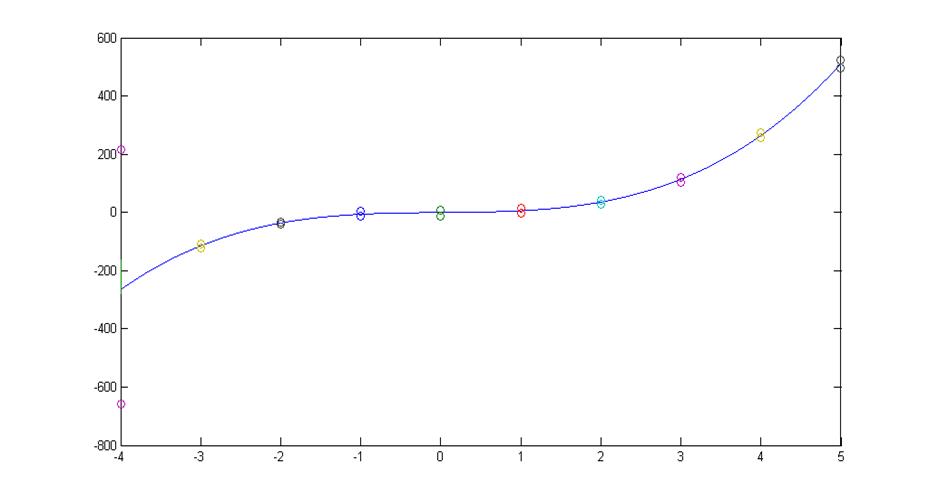
о - доверительные интервалы для мат. ожидания.
Рис. 2.1 Аппроксимирующий полином степени p=3
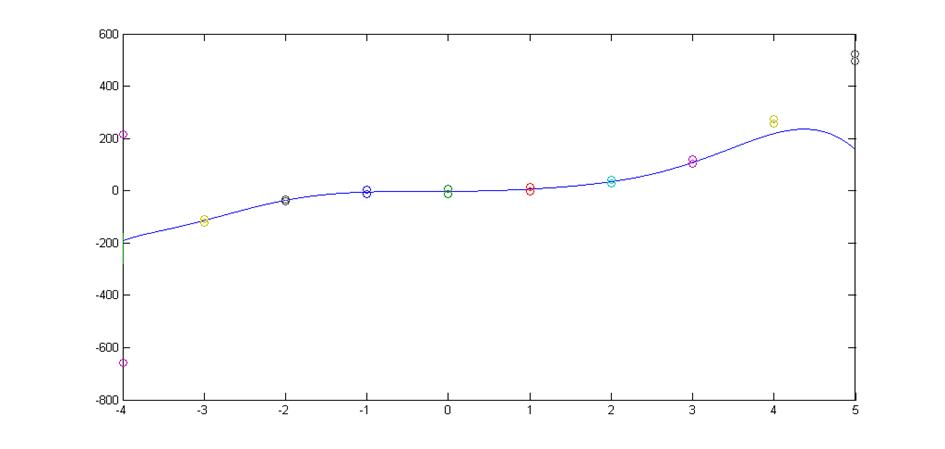
о - доверительные интервалы для мат. ожидания.
Рис. 2.2 Полином безизбыточной степени p=9
В ходе работы также были получены ковариационная и корреляционная матрицы для оценок коэффициентов полинома. В корреляционной матрице присутствуют разные элементы: как близкие по модулю к единице, так и близкие к нулю. Это означает, что некоторые коэффициенты все-таки в значительной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.