Разработка системы поиска экстремума по двум координатам с использованием метода Гаусса-Зейделя

Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

ОТЧЕТ

по курсовой работе на тему

Разработка системы  поиска экстремума по двум координатам с использованием метода Гаусса-Зейделя

Проектирование компьютерных систем управления

Студент гр. 5081/10

                                                                       Зачтено ________________________

                                                                       Преподаватель проф.

2011

1.  Техническое задание

1.1.  Формулировка задания

Разработать систему  экстремального поиска по двум координатам с использованием метода Гаусса-Зейделя. Поверхность поиска и возмущающее воздействие моделируются математически.

·  Уровень 1 – параметры алгоритма, поверхности поиска и возмущения фиксированы.

·  Уровень 2 – указанные параметры задаются в режиме выполнения.

·  Уровень 3 – обеспечивается оптимизация параметров алгоритма поиска.

Для уровней 2 и 3 предусмотреть в режиме выполнения по кнопке два подрежима – задания параметров и режим поиска.

Для задания исходных данных использовать диалоговое окно со встроенной справкой.

Поверхность возмущения задается уравнениями, представленными ниже:

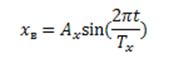
Уравнение минимизируемого функционала:

1.2.  Требования к обработке ошибок задания исходных данных

При работе системы все параметры должны проверяться на корректность. Параметры Ax, Ay должны контролироваться на неотрицательность. В случае, если они задаются отрицательными необходимо выдать соответствующее уведомление о некорректности и проинвертировать их значения на положительные. Параметры Tx и Ty также имеют ограничение снизу. В соответствии с теоремой Котельникова периоды Tx,Ty должны быть не меньше чем 50T₀, где T₀ – период сканирования задачи. В случае, если пользователь задал недопустимые значения, необходимо выдать уведомление о некорректности заданного значения, указать на допустимый интервал и приравнять к наименьшему значению из допустимого интервала.  Параметры Kx,Ky, исходя из уравнения для функционала, должны быть одного знака. При моделировании также потребуется значения шага моделирования по каждой из координат, а также первого пробного шага. Все эти параметры также не могут быть отрицательными. Если какой либо из этих параметров был задан отрицательным, то необходимо выдать соответствующее уведомление о некорректности и инвертировать на положительное значение. Начальные значения для системы также не могут быть отрицательными, и в случае некорректности, инвертироваться способом, описанным выше.

2.  Основные теоретические положения

Основной задачей работы программы при нахождении экстремума  является минимизация функционала

начало

Учитывая, что возмущающее воздействие в общем случае изменяется во времени, а значит изменяется и точка экстремума функционала, то необходимо постоянно контролировать значение функционала на предмет его возможной минимизации. Поэтому необходимо постоянно производить корректировку координат x и y. Для этого будем использовать алгоритм Гаусса-Зейделя, который заключатся в том, чтобы на каждом шаге  изменять одну из координат. При этом возможны два режима. Первый заключается в оптимизации длины шага, т.е. шаг будет изменяться во времени и выбираться исходя из максимальной минимизации функционала. Плюсом данного подхода можно назвать его гибкость, т.е. не нужно подбирать длину шага. Но не все технические объекты могут резко изменять менять свои параметры, поэтому также существует второй режим с постоянной длиной шага. Все вышесказанное можно изобразить схематически как:

 

3.  Проектирование

3.1.  Используемый инструментарий

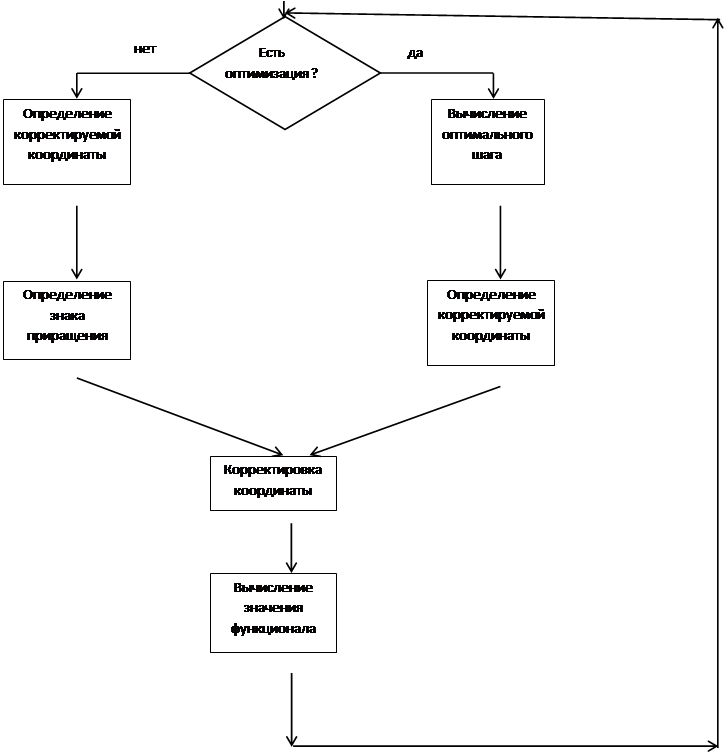(перечень блоков, использованных в окнах задач и отображения; подробное описание блоков, использованных в окнах задач и отображения, не описанных в учебном пособии; для остальных блоков – ссылка на учебное пособие с привязкой к страницам; конфигурация блоков – сослаться на проект)

При проектировании в среде разработки Advantech GeniDAQ Demo для разработки задач были использованы следующие блоки:

·  Timer Block. Функциональный блок таймера редактора задач предназначен для реализации таймеров различных типов и имеет вход сброса. Таймер может выполнять функции формирования абсолютных или относительных временных интервалов с разрешением 0.1 секунды или 1 секунда. Цикл таймера до сброса с последующим возобновлением работы может составлять от 1 минуты до 1 года. Содержимое таймера (относительное или абсолютное время) может быть передано другому функциональному блоку стратегии. Выходное значение блока таймера представляется в виде длинного целого значения в диапазоне от 0 до 4294967295. Данный блок является весьма удобным средством для реализации различных алгоритмов управления, выполнение которых основывается на интервалах времени[1]

·  Basic Script. Бейсик-процедура автоматически включается в программный проект при включении в задачу приложения функционального блока BASIC Script. Таким образом, число Бейсик-процедур программного проекта совпадает с общим числом функциональных блоков BASIC Script в приложении. Использование Бейсик-процедур обеспечивает максимальную гибкость при программировании специализированных вычислительных процедур и процедур сбора данных и управления[2]

·  Tag Block. Средства работы с тегами предназначены для получения доступа к функциональным блокам и другим тегам, расположенным в центре обработки данных SCADA-системы. Они могут применяться в любой компоненте программного проекта. Понятие тег в определенном контексте может ассоциироваться как с идентификатором объекта (имя тега), так и с самим объектом определенного типа (класса)[3]

·  Single Operation Calculation

При разработке экрана отображения были использованы компоненты «Trend Graph», «Text String», «Conditional Text», «Numeric String», «Binary Button». [4]