Расчет многомерной системы управления. Матрица передаточных функций и уравнения состояния

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

Расчетное задание №1

Дисциплина: Оптимальные системы управления

Тема: Расчет многомерной системы управления

Выполнил студент гр. 5081/1                                                                                 

Проверил:                                                                                                                 

Санкт-Петербург

2009

1.  Постановка задания

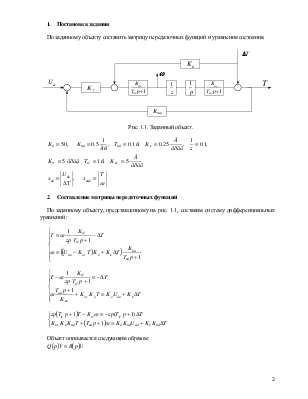
По заданному объекту составить матрицу передаточных функций и уравнения состояния.

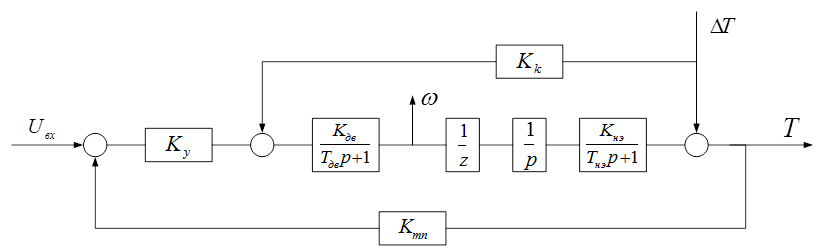
Рис. 1.1. Заданный объект.

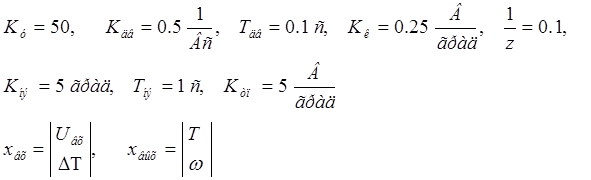
2.    Составление матрицы передаточных функций

По заданному объекту, представленному на рис. 1.1, составим систему дифференциальных уравнений:

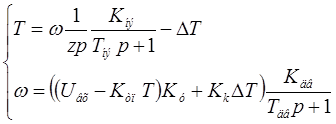
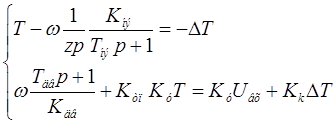
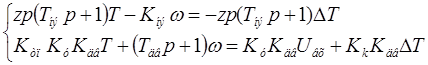
Объект описывается следующим образом:

Из полученной системы дифференциальных уравнений составим матрицы Q и R:

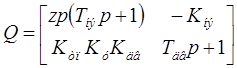
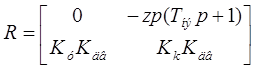
Подставим исходные данные в матрицы:

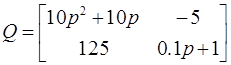
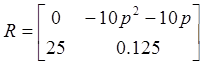
Найдем матрицу передаточных функций:

Поиск обратной матрицы:

- обратная матрица

 - определитель Q

  -  союзная матрица

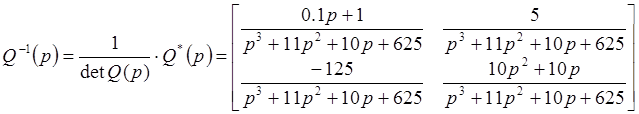
Передаточная матрица:

3. Описание объекта с помощью уравнений состояния

Заданный объект описывается следующей системой дифференциальных уравнений:

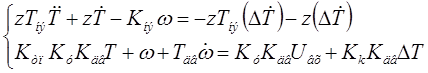
Cоставим матрицы коэффициентов для переменных входа и выхода при степенях производной 0, 1 и 2:

Коэффициенты при 2-ой производной:

Коэффициенты при 1-ой производной:

Коэффициенты при 0-ой производной:

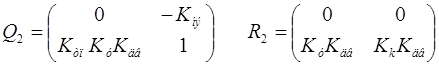
Вектора переменных состояния:

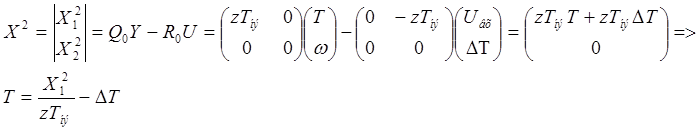
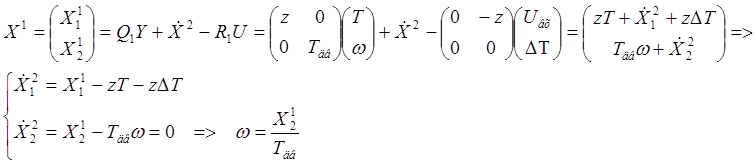
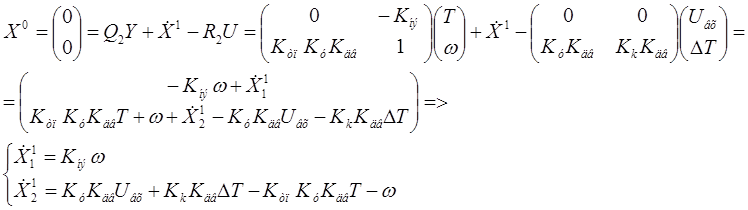
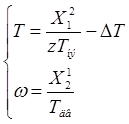
Получили систему уравнений состояния:

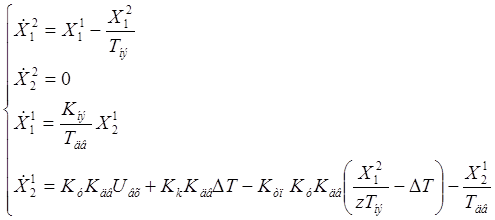
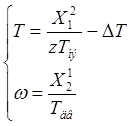
Матрица входа по состоянию:

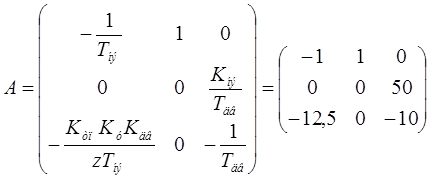
Матрица входа по управлению:

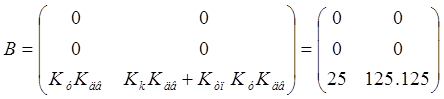
Матрица выхода по состоянию:

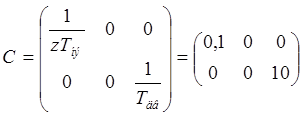
Матрица компенсации:

Для проверки найдем матрицу передаточных функций:

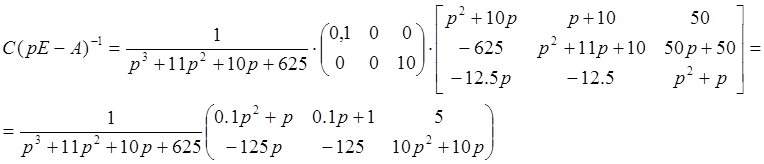
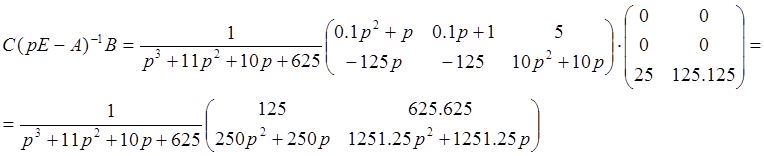
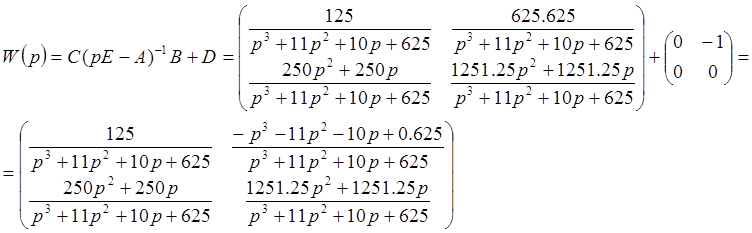
Передаточная матрица совпадает с матрицей, рассчитанной в предыдущем пункте.

4. Проверка правильности расчетов

Для проверки правильности расчетов составим модель исследуемой системы в Simulink и получим переходные характеристики по возможным комбинациям входных и выходных величин.

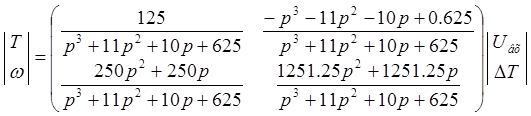
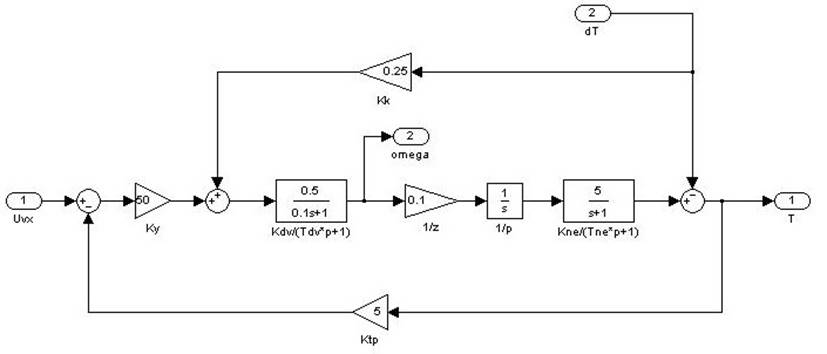
Рис. 4.1.1. Схема объекта (subsystem) в Simulink.

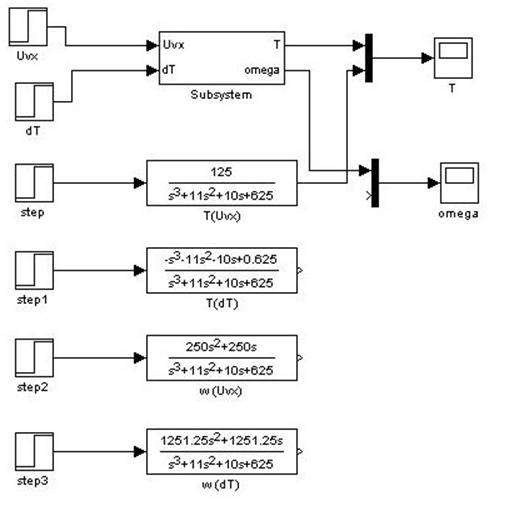
Рис. 4.1.2. Модель для исследования переходной характеристики  относительно .

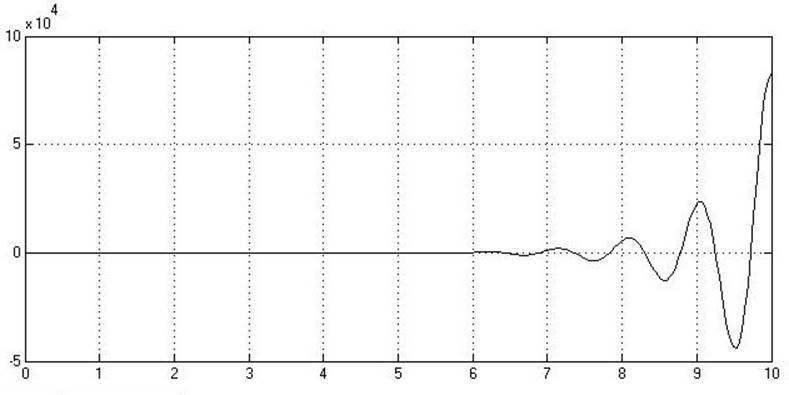
Рис. 4.1.3. Переходная характеристика  относительно .

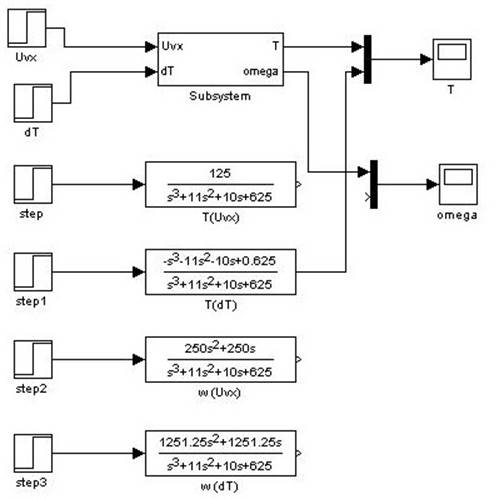
Рис. 4.1.4. Модель для исследования переходной характеристики  относительно .

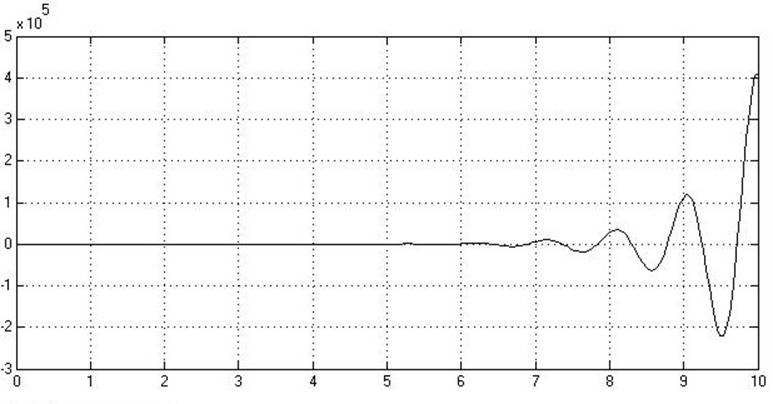
Рис. 4.1.5. Переходная характеристика  относительно .

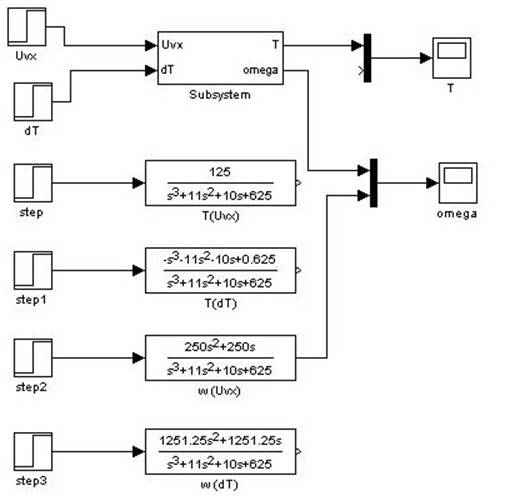
Рис. 4.1.6. Модель для исследования переходной характеристики  относительно .

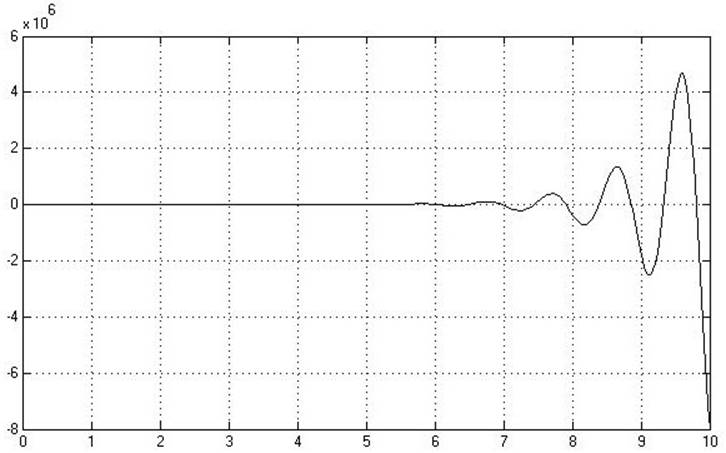
Рис. 4.1.7. Переходная характеристика   относительно .

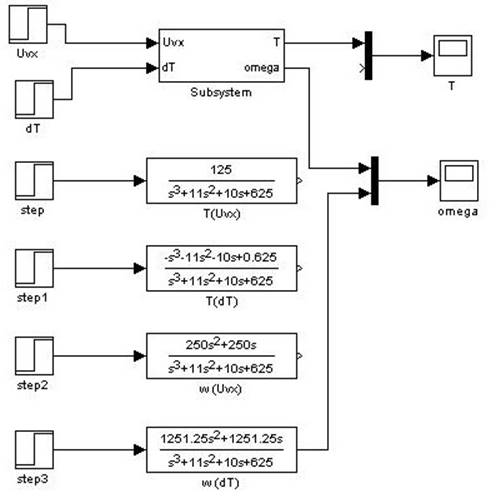
Рис. 4.1.8. Модель для исследования переходной характеристики   относительно .

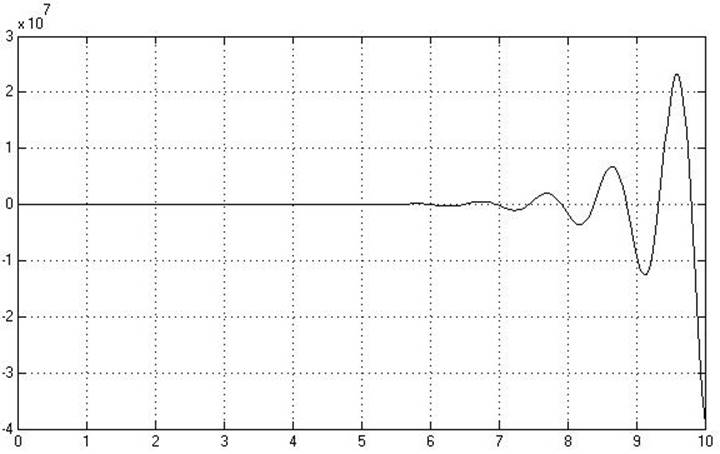
Рис. 4.1.9. Переходная характеристика   относительно .

Переходные процессы элементов матрицы передаточной функции совпадают с переходными процессами модели системы, что говорит о правильности вычисления W(p).