Расчет показателей надежности системы с помощью теории случайных процессов. График изменения вероятностной функции для различных состояний с помощью SciLab

Санкт-Петербургский государственный политехнический университет

Кафедра компьютерных систем и программных технологий

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2

Дисциплина: Надежность систем и устройств

Тема: Расчет показателей надежности системы с помощью теории случайных процессов 

Вариант 3

Выполнила студентка гр. 5081/1                                                                   

Проверил                                                                                                         

Санкт-Петербург

2012

1.  Цель работы:

Получение практических навыков анализа структурно-сложных систем, с целью достижения требуемого уровня надежности системы с минимальными затратами.

2.  Программа работы

·  Составить граф состояний.

·  Построить систему дифференциальных уравнений.

·  Решить систему с помощью SciLab.

·  Построить график изменения вероятностной функции для различных состояний с помощью SciLab.

3.  Исходные данные

Лифт осуществляет подъем груза. Лифт может находиться в двух состояниях:

• ожидание (в среднем длится 10 мин)
• подъем или спуск на нужный этаж (в среднем длится 3 мин)

В процессе работы могут возникать следующие проблемы:

• "застревание" лифта между этажами (частота 1 раз в 1000 суток)
• заклинивание дверей (частота 1 раз в 500 суток)
• авария (обрыв троса) (частота 1 раз в 3000 суток)

Считать, что при аварии (обрыве троса), когда лифт находится на первом этаже (принять вероятность этого за 10%), возможен ремонт (в течении 4-х дней), в других состояниях авария приводит к не ремонтируемому состоянию. Заклинивание дверей во время движения никак не влияет на движение лифта к нужному этажу. Заклинивание дверей или останов являются ремонтируемыми состояниями (среднее время ремонта 1 день).

Рассчитать вероятность работоспособного состояния лифта через 1,2,3,5 и 10 лет.

4.  Выполнение работы

Система может находиться в следующих состояниях:

1 – ожидание

2 – подъем

3 – застревание

4 – заклинивание дверей

5 – авария

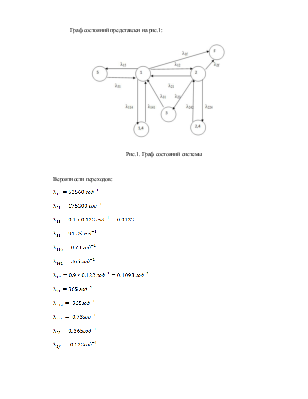
Граф состояний представлен на рис.1:

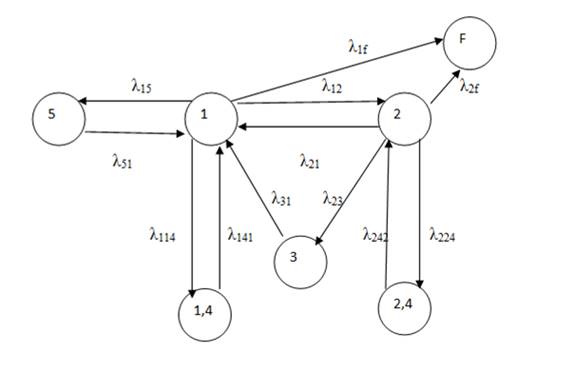
Рис.1. Граф состояний системы

Вероятности переходов:

Система дифференциальных уравнений:

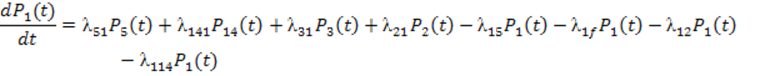
Подставим числовые данные и упростим:

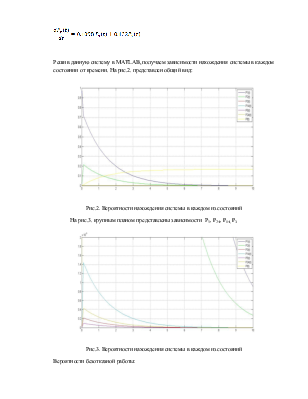
Решив данную систему в MATLAB, получаем зависимости нахождения системы в каждом состоянии от времени. На рис.2. представлен общий вид:

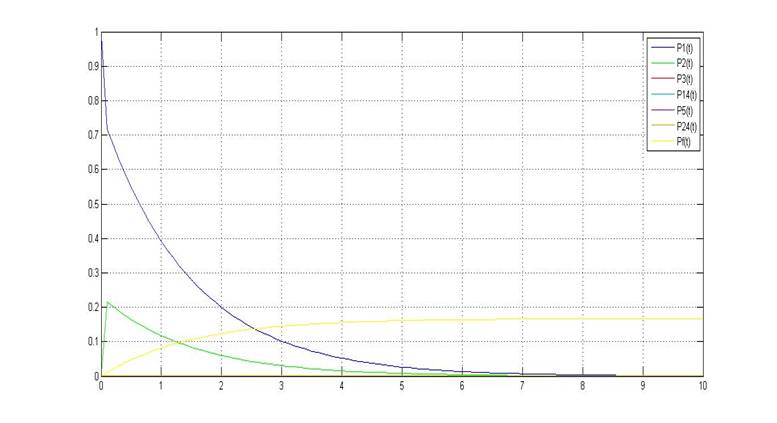
Рис.2. Вероятности нахождения системы в каждом из состояний

На рис.3. крупным планом представлены зависимости  P₅, P₂₄, P_14, P₃

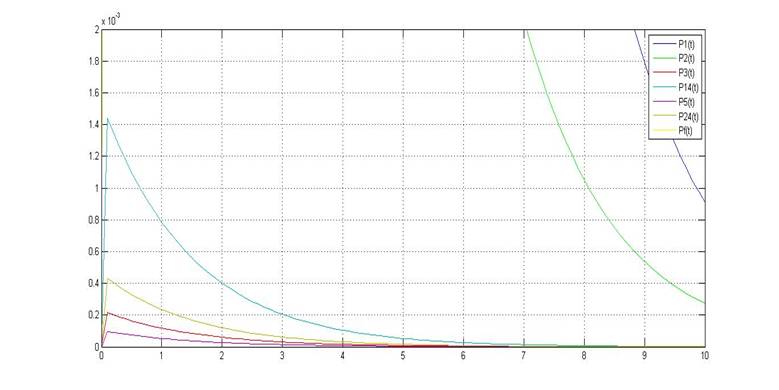
Рис.3. Вероятности нахождения системы в каждом из состояний

Вероятности безотказной работы:

Через 1 год – 0.9181

Через 2 года – 0.8764

Через 3 года –  0.8551

Через 5 лет –  0.8387

Через 10 лет –  0.8332

5.  Вывод

Анализируя полученные зависимости, можно сделать вывод о том, что со временем вероятность нахождения лифта в работоспособном состоянии уменьшается, а вероятность аварии, напротив, увеличивается. Вероятность нахождения в ремонте по различным причинам в первое время эксплуатации больше, чем в дальнейшем.