Информатика и выч. техника \ Моделирование систем управления

Моделирование детерминированных процессов. Моделирование процессов первого порядка. Результаты моделирования

Страницы работы

14 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 7

Дисциплина: моделирование СУ

Тема: Моделирование детерминированных процессов

Выполнили ст. группы 4081/2:

Преподаватель:

_______2008 г.

Санкт-Петербург 2008

1. Вариант задания

Вариант	Функция
25		1	0,25	0,5

2. Выполнение работы

2.1. Моделирование процессов первого порядка

Построенная модель g0:

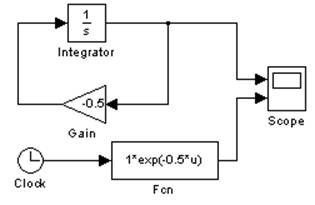
Результаты моделирования:

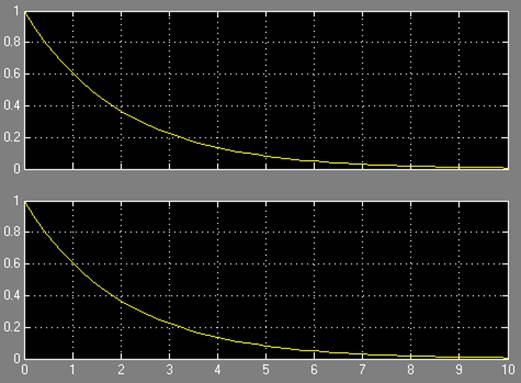
Результаты моделирования при a = 0.5:

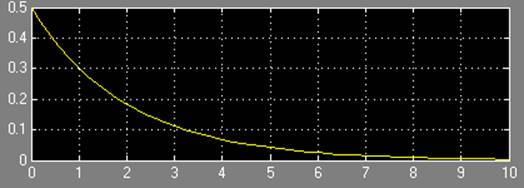
Результаты моделирования при a = 0,25:

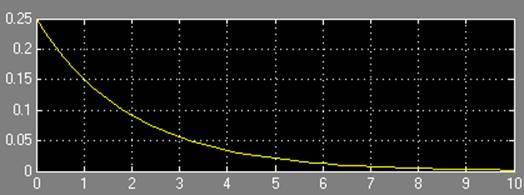
Результаты моделирования при c = 1:

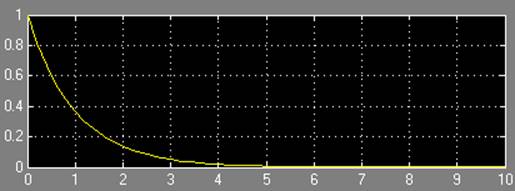
Результаты моделирования при c = 0,1:

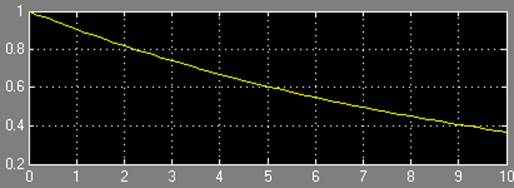
2.2. Моделирование процессов третьего порядка

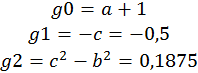
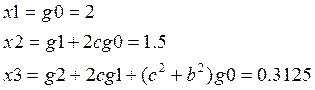
Построенная модель g1:

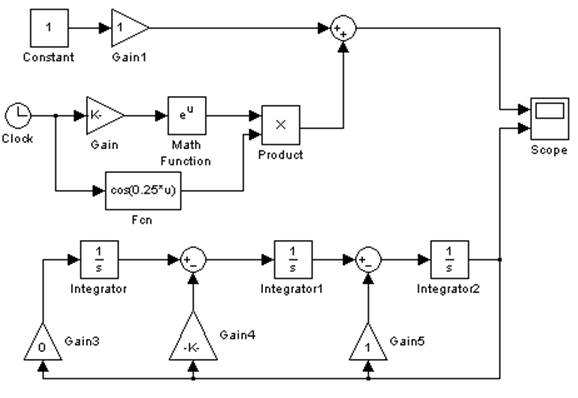
Результаты моделирования:

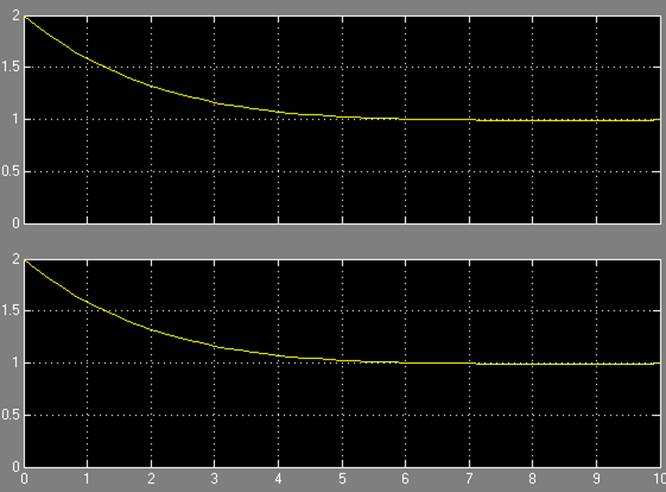
Результаты моделирования при a = 0,1:

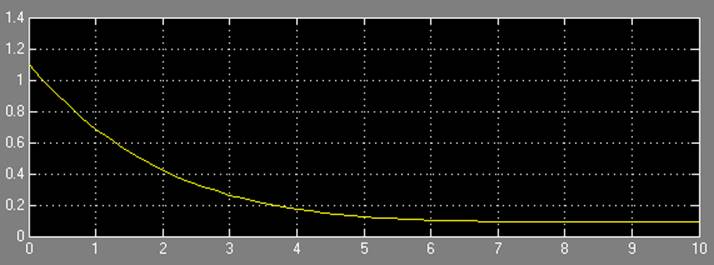
Результаты моделирования при a = 0,5:

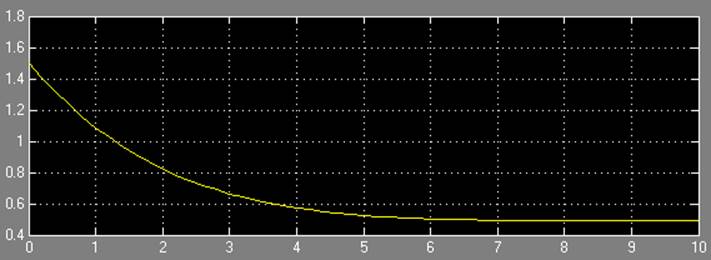
Результаты моделирования при b = 0,5:

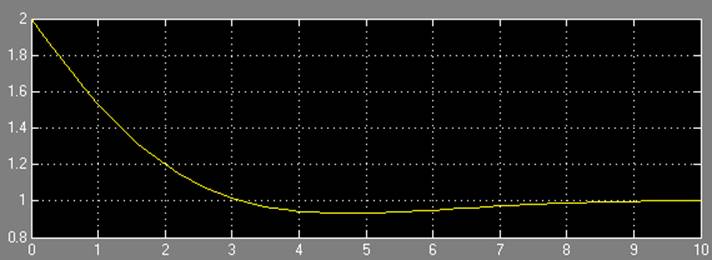
Результаты моделирования при b = 1:

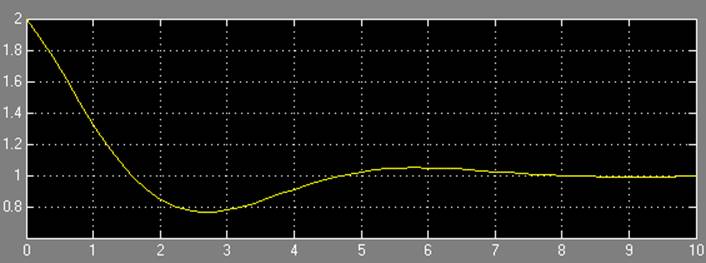
Результаты моделирования при c = 0,1:

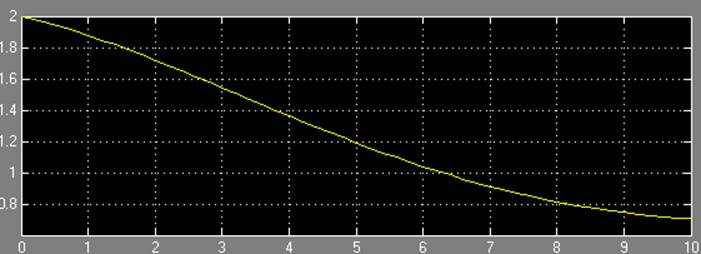
Результаты моделирования при c = 1:

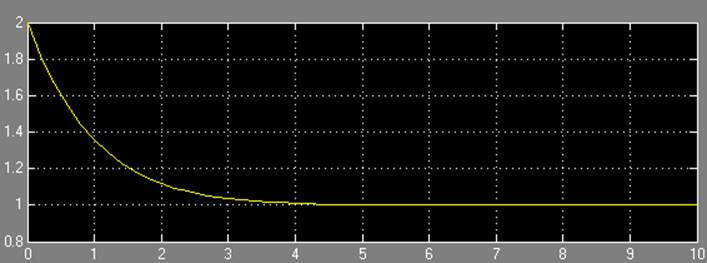
2.3. Линейно-параметрическая модель

Для заданной функции в соответствии с вариантом исходных данных и выбранным многочленом μ(s) получить аналитическое выражение математической модели.

Задана функция μ(s) – непрерывный во времени детерминированный процесс, заданный своим аналитическим выражением. Изображение данного процесса по Лапласу есть:

Пусть μ(s) – произвольный устойчивый полином третьей степени. Запишем тождество:

Подставим в изображение по Лапласу заданного процесса числовые значения коэффициентов:

Выберем полином μ(s) = (s+1)(s+2)(s+3) и перепишем тождество в виде:

Представим соотношение в виде:

Тогда:

Где

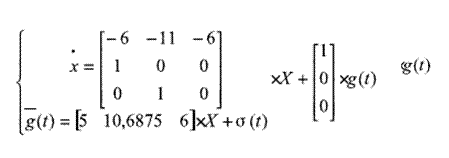Найдем выражение для σ(t):

>> syms s

>> ilaplace((2*s^2+1.5*s+0.3125)/(s^3+6*s^2+11*s+6))

ans =

13/32*exp(-t)-85/16*exp(-2*t)+221/32*exp(-3*t)

>> pretty(ans)

13 85 221

-- exp(-t) - -- exp(-2 t) + --- exp(-3 t)

32 16 32

Построенная линейно-параметрическая модель g1:

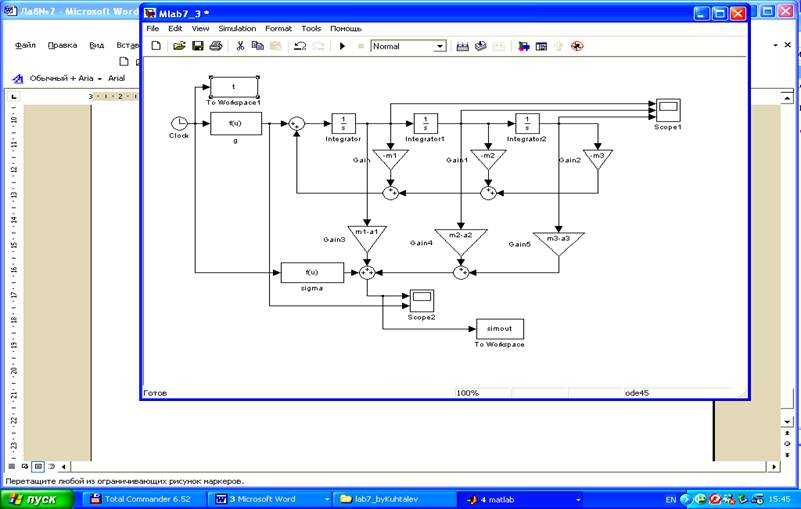
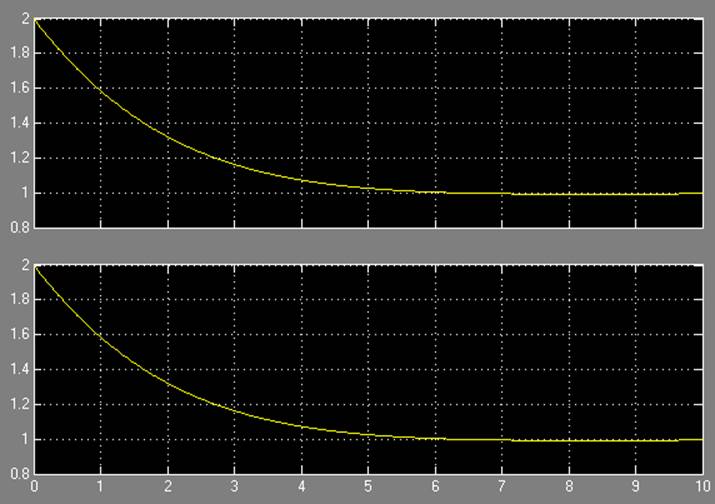
Результаты моделирования:

Переменные состояния:

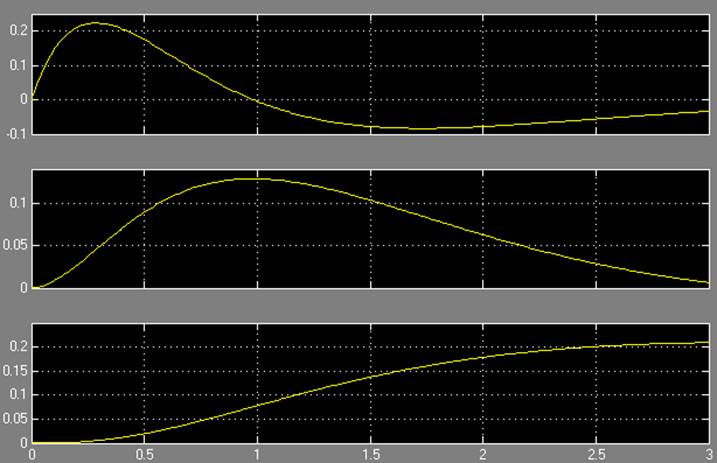
Результаты моделирования при a = 0,5:

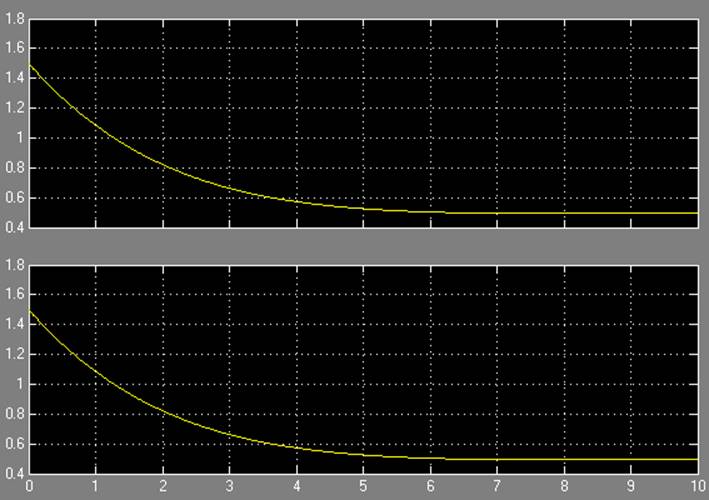
Результаты моделирования при b = 1:

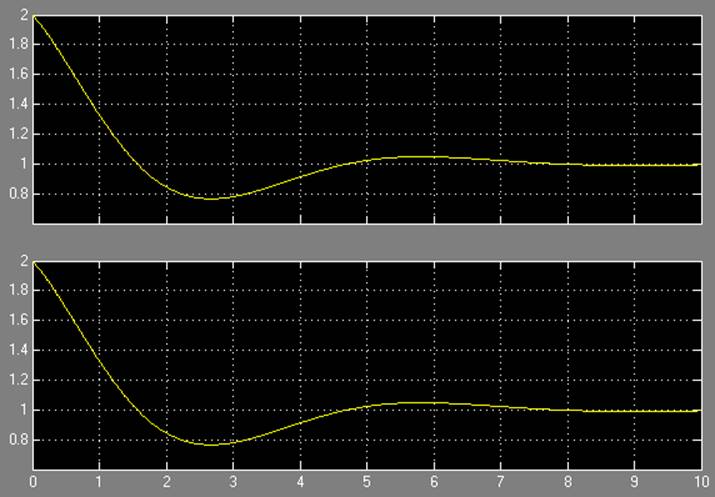
Результаты моделирования при c = 1:

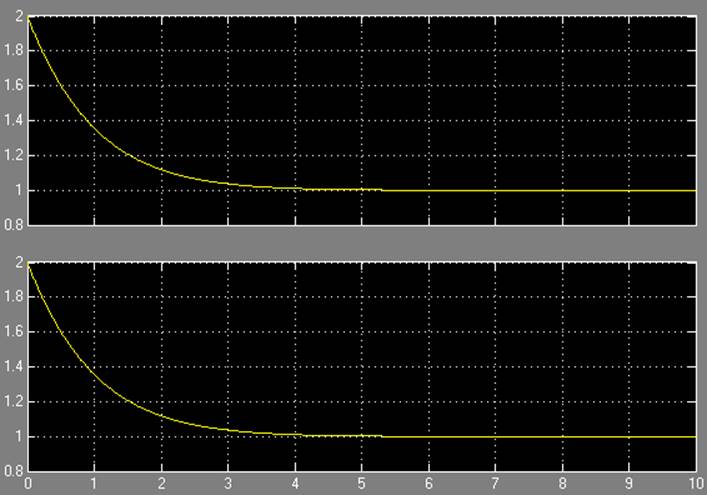
Изменим параметры полинома μ(s):

m1 = 9, m2 = 23, m3 = 15

Результаты моделирования:

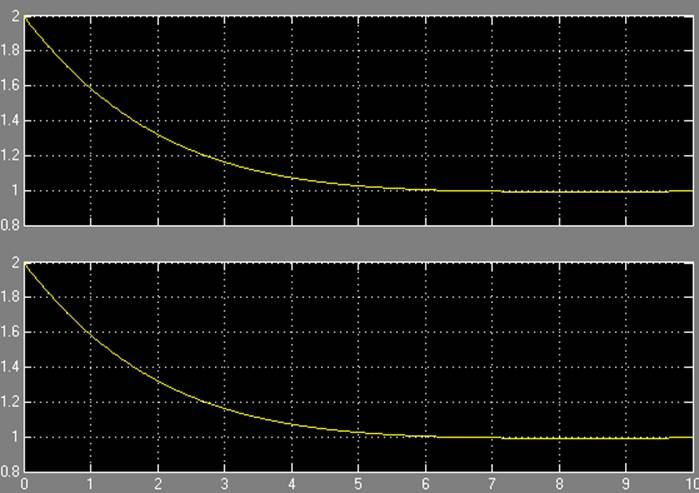
2.4. Определите, с какого момента времени сигнал выхода модели совпадает с линейно-параметрическим представлением исходного процесса. При каких параметрах многочлена оно будет наименьшим

Для определения времени, начиная с которого происходит совпадение значений сигнала выхода модели g(t) и линейно-параметрическим представлением исходного процесса, использовался следующий скрипт:

function analyze( simout, tout, g )

delta = 0.001;

time_index = -1;

for(i=length(tout):-1:1)

if((simout(i)-g(i))/simout(i)>=delta)

time_index = i+1;

break;

end;

if(time_index == -1)

time = 0

else

if(time_index > length(tout))

time_index = length(tout);

end;

time = tout(time_index)

end;

return;

μ(s)	μ1	μ2	μ3	t
(s+1)(s+2)(s+3)	6	11	6	0
(s+1)(s+3)(s+5)	9	23	15	1.8931
(s+2)(s+4)(s+9)	15	62	72	1.5031
(s+1)(s+2)(s+20)	23	62	40	2.1231
(s+5)(s+6)(s+7)	18	107	210	2.1931
(s+2)(s+3)(s+4)	9	26	24	1.5431

μ(s)=(s+2)(s+4)(s+9):

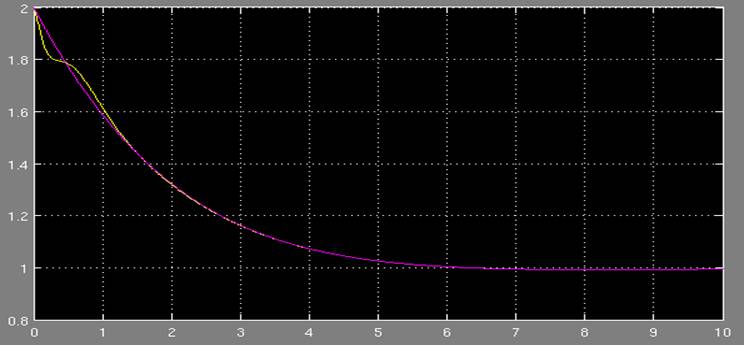μ(s)=(s+1)(s+2)(s+3):

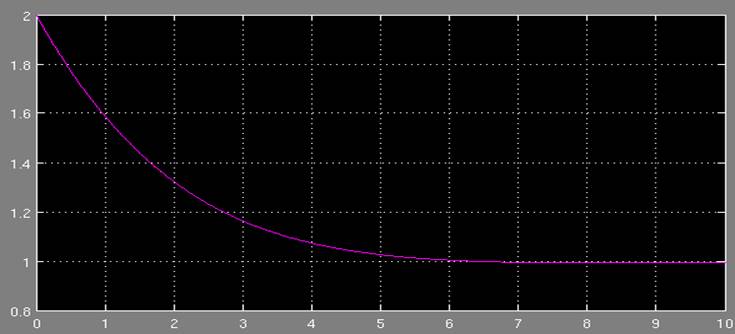
3. Выводы

В результате работы были получены навыки построения моделей заданных процессов. В результате исследования моделей были подтверждены теоретические представления, что говорит о правильности построения модели.