Нейроны и функции активации. Значения синоптического коэффициента и порога и задавая необходимый тип функции активации

Neuron Model and Network Architectures

Neurons

Нейроны и функции активации

(Simple neuron and transfer functions, filename: nnd2n1)

Входы р, скалярные, вместе с синоптическими коэффициентами w образуют произведение wp, которое тоже является скаляром. Оно суммируется со значением b (порог), который вводится как еще один вход. Результат суммирования - скаляр n, который является аргументом функции активации F. На выходе мы получаем а.

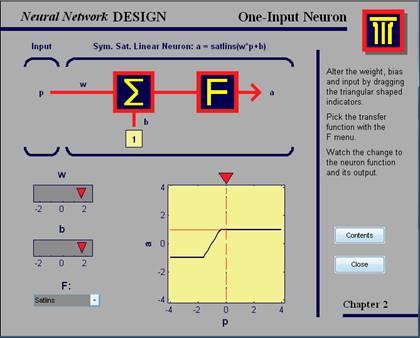
Рис.1. демонстрация nnd2n1

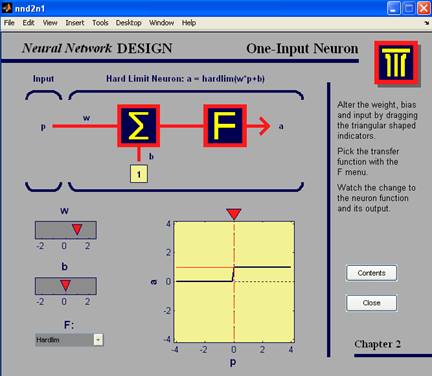
Рис.2. демонстрация nnd2n1

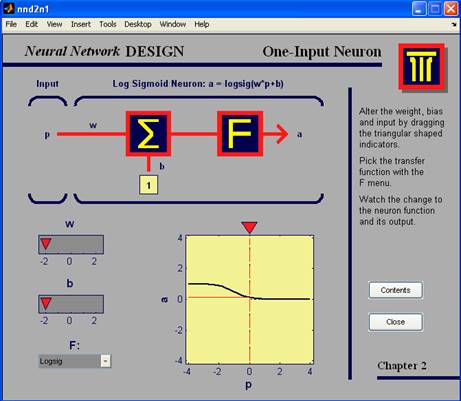
Рис.3. демонстрация nnd2n1

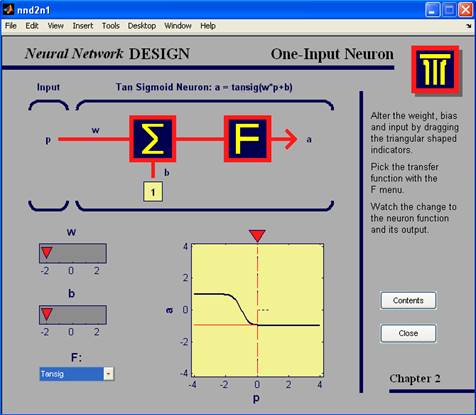
Рис.4. демонстрация nnd2n1

Меняя значения синоптического коэффициента и порога и задавая необходимый тип функции активации, получаем желаемый результат на графике.

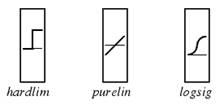
Функции активации:

hardlim – пороговая

hardlims – пороговая с насыщением

purelin – линейная

satlin – линейная с насыщением

satlins – линейная симметричная

logsig – сигмоидальная

tansig – сигмоидальная симметричная (гиперболический тангенс)

Нейронные сети с векторными входными данными

(Neuron with vector input, filename: nnd2n2)

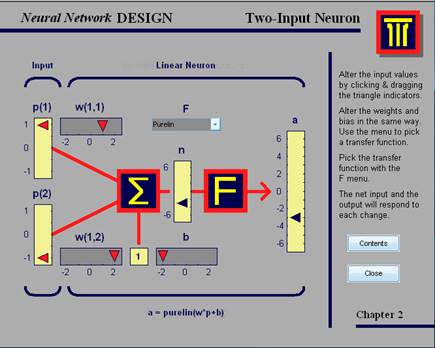
Рис.5. демонстрация nnd2n2

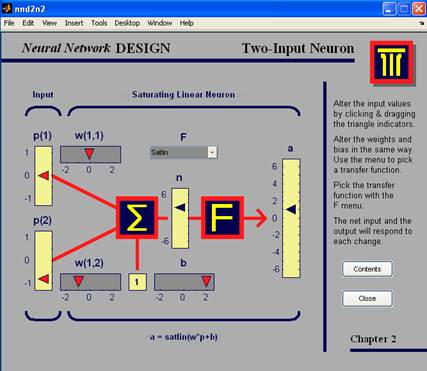
Рис.6. демонстрация nnd2n2

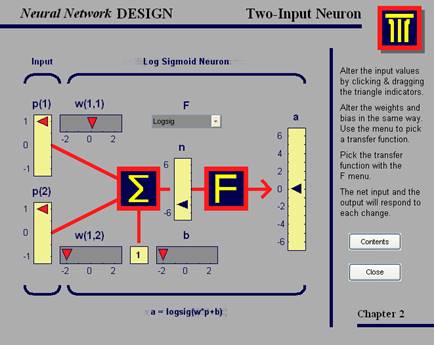
Рис.7. демонстрация nnd2n2

P – входной вектор. В демонстрации у него два составляющих: р1 и р2 (говорят, что р – это вектор R входных значений, R = 2), значения которых пользователь может менять в диапазоне [-1; 1]. Как и в предыдущем случае, каждое входное значение перемножается с соответствующим коэффициентом из матрицы W, (в данном случае: w1 и w2), суммируется со значением b и на выходе получается некоторое значение n, которое является аргументом функции активации F. На выходе получаем а, соответствующее установленным значениям р1, р1, w(1,1), w(1,2), b и выбранной функции.

Perceptrons

Границы решения

(Decision boundaries, filename: nnd4db)

Каждый вход персептрона перемножается с соответствующим синоптическим коэффициентом, и сумма этих произведений поступает на вход пороговой функции активации, которая также получает на вход единицу с входа b.

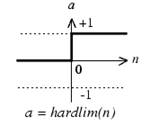
Рис. 8. пороговая функция активации, на выходе которой 0 или 1

Пороговая функция активации дает возможность персептрону классифицировать вектор входа путем разделения области входных значений на две части. Выходные значения будут равны 0, если вход n функции будет меньше нуля, и 1, если больше или равен нулю.

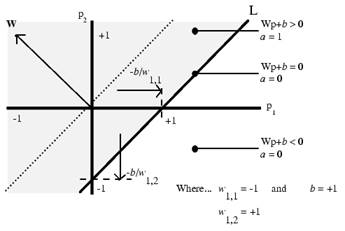
Рис. 9. пример пороговой функции активации с двумя входами, w(1,1)=-1, w(1,2)=1, b=1

Прямая L – граница решения, которая делит всю область на 2 части. Эта прямая перпендикулярна матрице коэффициентов W и смещена в соответствии со значениями порогов b. Входные вектора, располагающиеся в верхней левой области, будут соответствовать выходному значению, равному 1; векторы в нижней правой области – соответствующие 0. Разделительная прямая может быть перемещена куда угодно для классификации входных значений желаемым образом путем задания коэффициента и порогового значения.

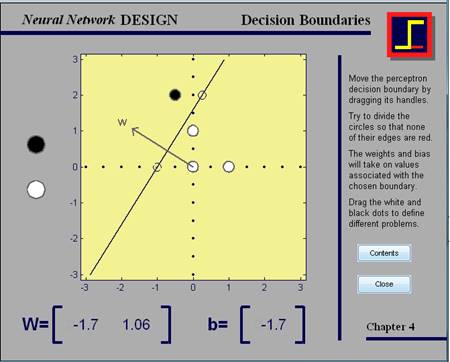
Рис. 10. демонстрация nnd4db

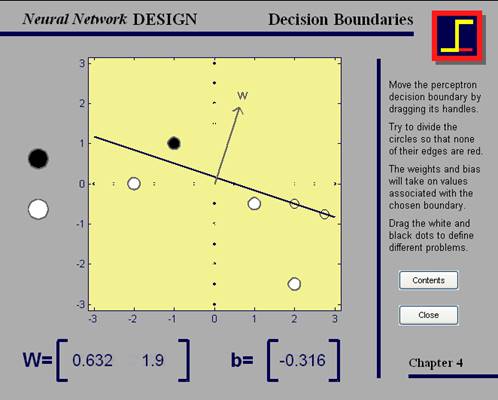
Рис. 11. демонстрация nnd4db

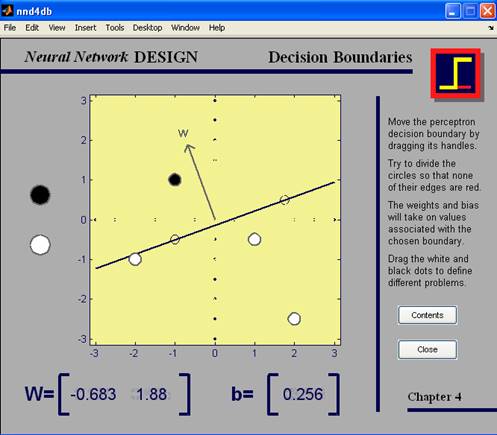
Рис. 12. демонстрация nnd4db

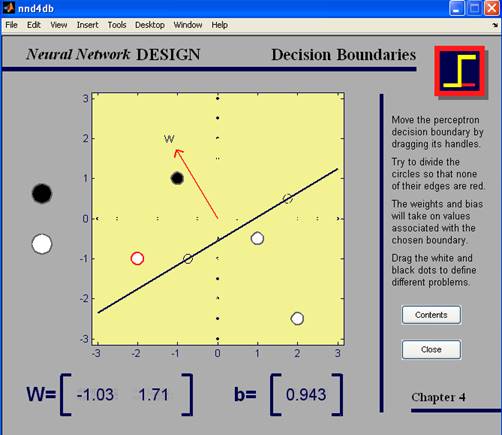
Рис. 13. демонстрация nnd4db

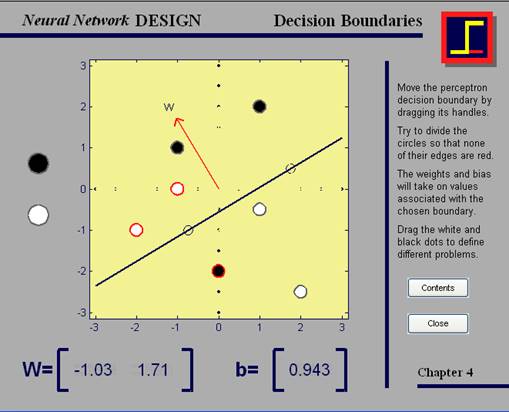
Рис. 14. демонстрация nnd4db

Если все сделано правильно, границы белых и черных кружков не должны быть красными. В этой демонстрации пользователь может перемещать границу решения, добавлять для классификации новые входы и наблюдать, как программа приводит в исполнение нейронную сеть, которая классифицирует входные векторы должным образом.

Правила обучения персептрона

(Perceptron learning rule. Pick boundaries, filename: nnd4pr)

Доказано, что правило персептрона сходится на конечном числе итераций, если решение существует.

Если не используется пороговое значение, то правило персептрона находит решение, используя только веса синоптических коэффициентов.

Подаем на вход персептрона такой вектор х, для которого уже известен правильный ответ. Если выходной сигнал персептрона совпадает с правильным ответом, то никаких действий не предпринимается. В случае ошибки происходит обучение персептрона.

Первое правило: Если на выходе персептрона получен 0, а правильный ответ равен 1, то необходимо увеличить веса связей между одновременно активными нейронами.

Второе правило: Если на выходе персептрона получена единица, а правильный ответ равен нулю, то необходимо уменьшить веса связей между одновременно активными нейронами.