Пределение функций преобразования средств измерений по экспериментальным данным

6.7.  Определение функций  преобразования

средств измерений  по экспериментальным данным

6.7.1. Исходные данные

Функция преобразования (или статическая характеристика преобразования) средства измерений - функция, описывающая зависимость между входным сигналом x и выходным сигналом y (показанием) средства измерений. Чаще всего она представляется  в  виде  y = f(x),  но  иногда  используется  и обратная функция x = y(y). Функции преобразования средств измерений кроме аналого-цифровых и цифроаналоговых преобразователей, - это гладкие дифференцируемые монотонные функции, сколь угодно точно аппроксимируемые степенными полиномами.

Определение статических характеристик преобразования средств измерений обычно выполняется при их калибровке в метрологических подразделениях с помощью образцовых средств, характеристики погрешности которых и методы выполняемых при этом измерений должны обеспечивать точность результатов измерений, превышающую ожидаемую (декларированную) точность испытуемого средства измерений не менее, чем в 3 ¸ 5 раз.

Пусть статическая характеристика преобразования  y=f(x) аппроксимируется степенным полиномом степени  p с неизвестными коэффициентами:

.                                         (35)

Задача состоит в определении значений коэффициентов степенного полинома по результатам измерений входного и выходного сигналов так, , чтобы во всех  i - ых точках выполнялись равенства:

,        i = 1,2,...,k.            (36)

Обычно в нормативных документах на испытуемое средство измерений указываются значения , которые должны быть заданы на входе. С помощью калибратора или иного точного источника входной величины x устанавливают последовательно указанные значения, начиная с наименьшего, и при каждом значении  измеряют выходной сигнал. Затем по достижении последнего k - го значения и измерения выходного сигнала ненамного увеличивают значение входной величины, и процесс повторяется в обратном направлении. Делают несколько таких циклов в одинаковых условиях. В результате при каждом значении входной величины будет получен массив выборочных значений выходной величины объемом n:

Рис. 15. Графическое представление результатов экспериментов по определению статической характеристики преобразования

. Пример графического представления результатов описанного эксперимента показан на рис. 15. Здесь ,i =  1,2,...,k; j = 1,2,...,n- обозначение выборочных значений выходной величины, полученных в  i - ой точке при j - ом эксперименте.

6.7.2. Определение функции  преобразования

Предварительная обработка данных, полученных в результате эксперимента и представленных на рис. 15, заключается в том, что в каждой i - ой точке вычисляются оценки математического ожидания и дисперсии (см. также п. 6.2)???:

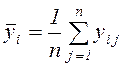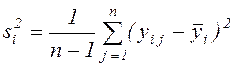            ,        .                              (37)

Результаты выполненной предварительной обработки исходных данных записывают в виде вектора средних значений и матрицы оценок дисперсий:

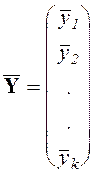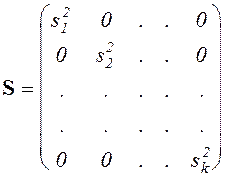,   .                               (38)

Равенства (36) образуют систему уравнений, которая может быть записана в матричном виде

,                                                     (39)

где вектор  определен в (38). Матрица X и вектор A имеют вид

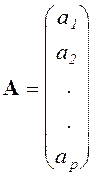, .                (40)

Всегда желательно, чтобы k > p + 1. Таким образом создается полезная избыточность, повышающая устойчивость оценок коэффициентов полинома. Но при этом матрица  X  неквадратная, и система (39) не имеет решения в обычном смысле. Для получения решения эту систему преобразуют к системе с квадратной матрицей путем умножения слева на транспонированную матрицу :

,

Решая эту систему, получают вектор оценок коэффициентов полинома:

.                                               (41)

Компонентами вектора  являются оценки  коэффициентов полинома (35). Описанный метод их получения называется методом наименьших квадратов (МНК), поскольку полином с такими коэффициентами пройдет между экспериментальными точками так, что сумма квадратов расстояний от него до этих точек окажется минимальным.

На практике точность измерений значений выходного сигнала при разных значениях входного сигнала может быть различной. Понятно, что более точным результатам следует придавать больший вес, чем менее точным. С этой целью в уравнение (41) вводится матрица S :

.                                      (42)

Дисперсии этих оценок  суть диагональные элементы матрицы

.                                               (43)

Появление множителя  1/n вызвано тем, что левая часть системы (36) и (39) - это вектор средних арифметических значений, дисперсия которых, как указано в п. 6.5.1, в n раз меньше дисперсии погрешности однократных измерений.

6.7.3. Определение коэффициента преобразования

      линейной функции.    

При разработке и изготовлении средств измерений обычно стремятся к тому, чтобы их функции преобразования были линейными по отношению к информативному параметру измеряемого или преобразуемого сигнала измеряемой величины. Мало того, обычно добиваются, чтобы эти функции обязательно проходили через начало координат.

Незначительная нелинейность и ненулевое значение выходного сигнала при нуле входного учитываются в составе систематической составляющей погрешности средства измерений. Значение этой погрешности зависит от входной величины и является