Синтез и исследование оптимальной системы ЛК-управления в непрерывном времени. Исследование компьютерных систем управления, страница 2

В эксперименте было принято, что вес управления (матрица R) остается неизменной. При увеличении матрицы коэффициентов Q увеличивается «штраф» на координаты объекта, поэтому коэффициенты ОС увеличиваются.

Исследование системы без регулятора (разомкнутой)

Теоретические графики:

>> A = [0 1; -1 -0.5];

>> B = [0; 1];

>> C = [0 1];

>> D = 0;

>> sys = ss(A,B,C,D);

>> impulse(sys);

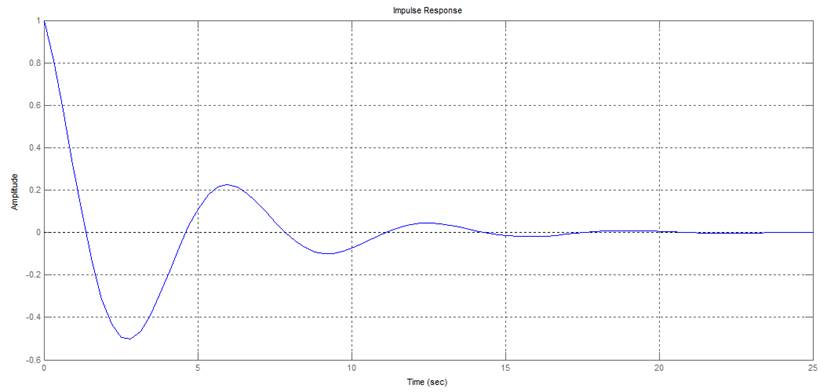
>> initial(sys,[1 0]);

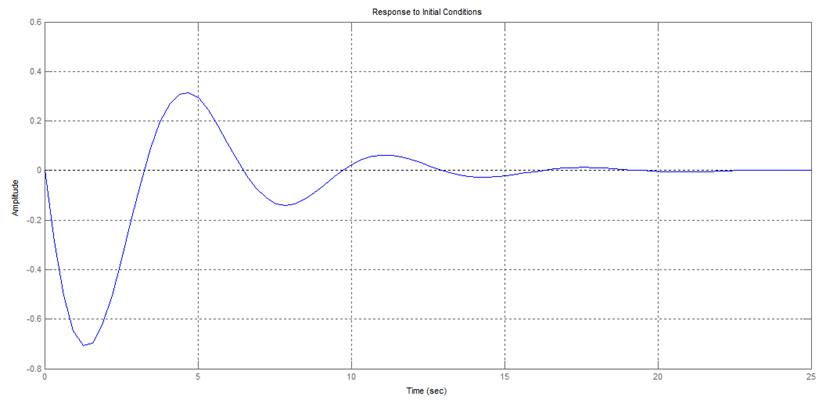
Экспериментальные графики:

Теоретические и экспериментальные зависимости совпадают, тем самым мы убедились в адекватности собранной модели объекта. Время переходного процесса составляет 14 секунд, максимальное перерегулирование 0.44 В.

Исследование переходных процессов в системе при вариациях коэффициентов обратной связи

Рассчитаем в Matlab оптимальные коэффициенты для заданных матриц Q и R и построим для них линии равного уровня. Найденные значения коэффициенов совпадают с рассчитанными  ранее вручую и полученными  с помощью программы в лаборатории. Значение критерия в этом случае: J = 1.540126895805001.

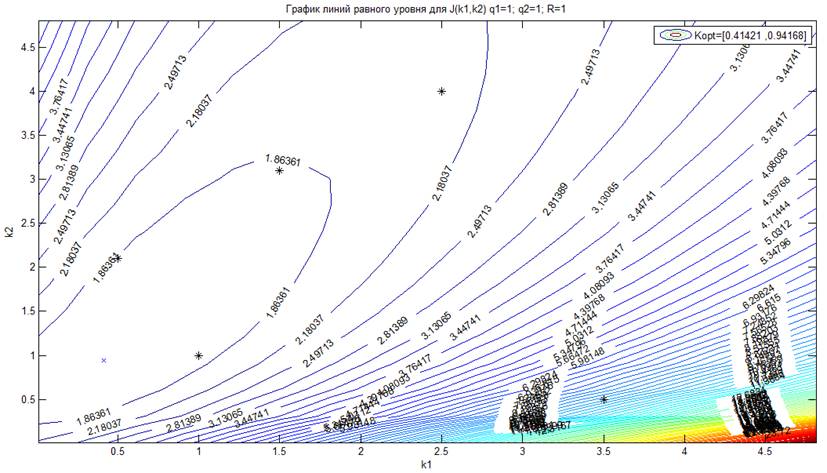
Установим рассчитанные значения коэффициентов обратной связи: К₁ = 0.415, К₂ = 0.945. Получившееся значение критерия: J = 1.57820

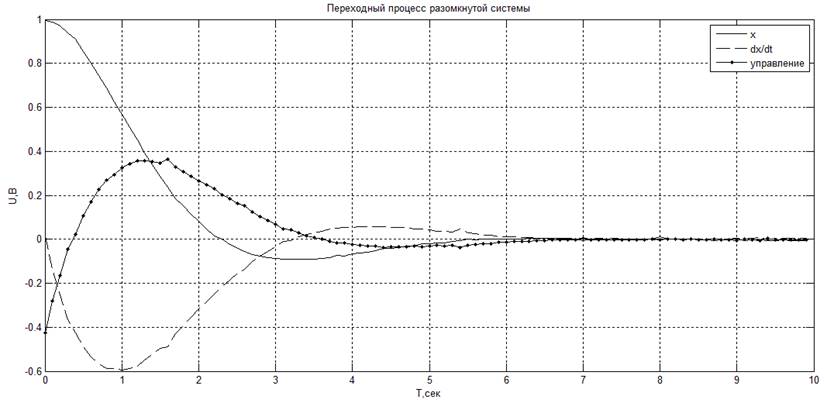
Время переходного процесса составило 4.5 секунды, максимальное перерегулирование – 0.09 В. Таким образом, можно сделать вывод, что использование регулятора существенно уменьшает данные параметры переходного процесса.

Теперь будем менять значения коэффициентов ОС (экспериментальные точки обозначены на рисунке с линиями равного уровня) и наблюдать, как при этом меняется значение критерия и вид переходного поцесса.

·  К₁ = 1, К₂ = 1. Получившееся значение критерия: J = 1.85251

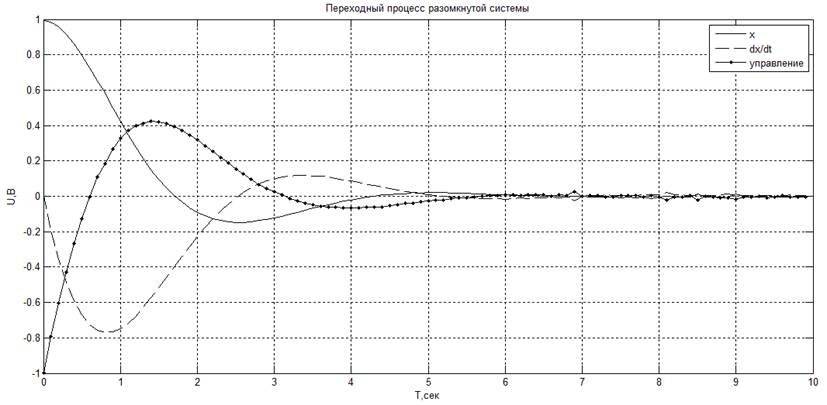
·  К₁ = 0.5, К₂ = 2.1. Получившееся значение критерия: J = 1.85184

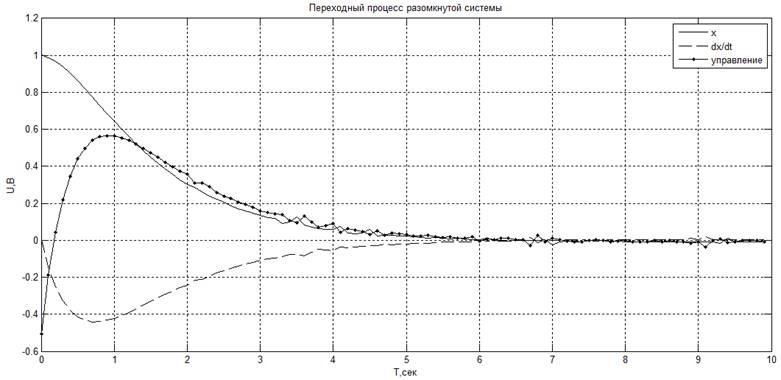
·  К₁ = 1.5, К₂ = 3.1. Получившееся значение критерия: J = 1.96764

·  К₁ = 2.5, К₂ = 4. Получившееся значение критерия: J = 2.11737

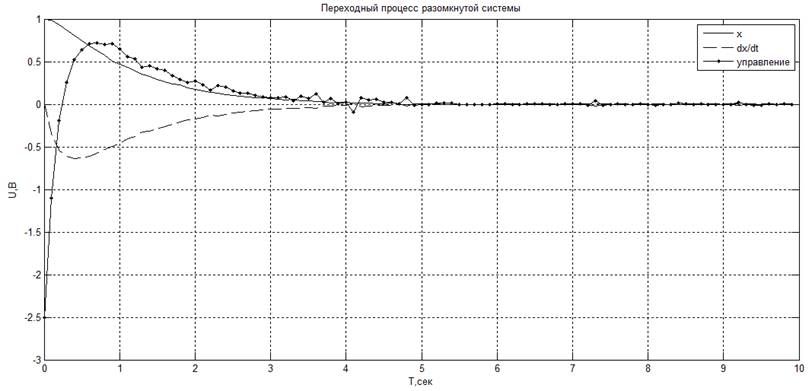
·  К₁ = 3.5, К₂ = 0.5. Получившееся значение критерия: J = 8.77845

Из получившихся графиков можно сделать вывод, что при оптимальных коэффициентах ОС значение критерия наименьшее. При отклонении коэффициентов от оптимальных значение критерия возрастает. Одновременно с этим параметры переходного процесса, такие как перерегулирование или время переходного процесса, могут улучшаться, а управление – ухудшаться. Это позволяет говорить о том, что при оптимальных коэффициентах ОС мы имеем наилучший баланс между отклонением координат объекта и затрачиваемым управлением.

Исследование переходных процессов в системе при вариациях матрицы Q

На рисунке представлены переходные процессы при разных значениях матрицы Q и, соответственно, разных оптимальных коэффициентах.

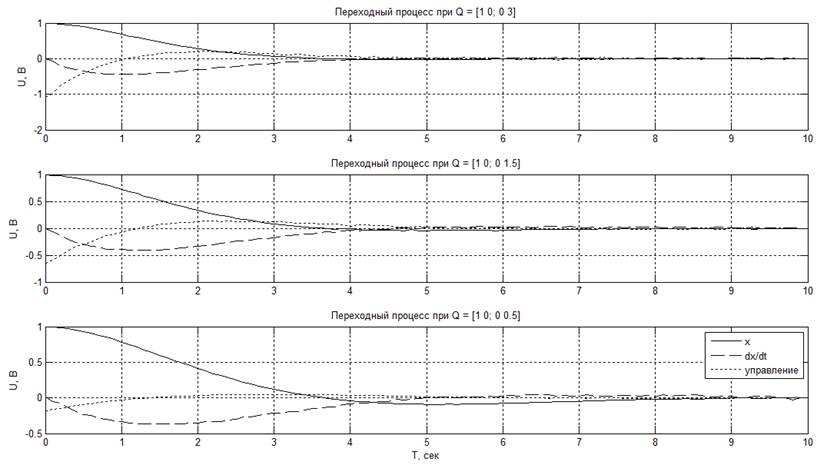
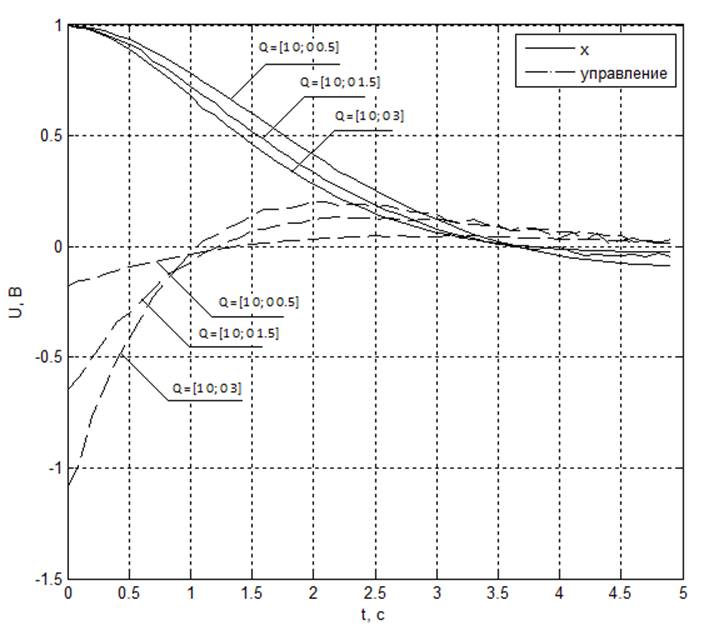
Из рисунков видно, что при увеличении веса координат по отношению к весу управления параметры переходного процесса объекта улучшаются: уменьшается колебательность и время переходного процесса, при этом управление, напротив, ухудшается.

Выводы

В работе производился синтез и изучение системы оптимального управления в непрерывном времени с интегральным квадратичным критерием качества.

Значение критерия важно при сравнении качества управления при одних и тех же условиях и заданных весовых коэфициентах управления и координаты критерия. Изменяя коэффициенты ОС, получаем различные кривые переходного процесса, площадь под которыми стремимся уменьшить (за счет уменьшения времени процесса и перерегулирования), поэтому минимум критерия дает оптимальные коэффициенты ОС.

Выполнение работы показало, что результат вычисления оптимальных коэффициентов с использованием уравнения Риккати не зависит от начальных значений коэффициентов. При большом отличии начальных коэффициентов от оптимальных увеличивается количество итераций, необходимое для вычисления оптимальных коэффициентов.

При различных требованиях к координате и управлению, которые задаются весами критерия J, получаем различные переходные процессы. Изменяя матрицу Q в уравнении Риккати, мы тем самым накладываем штраф на координаты объекта, поэтому коэффициенты ОС увеличиваются, вместе с ними изменяется и значение критерия.

При оптимальных коэффициентах ОС значение критерия наименьшее. При отклонении коэффициентов от оптимальных значение критерия возрастает, одновременно с этим изменяются параметры переходного процесса. Анализ получившихся в работе графиков позволяет сделать вывод о том, что  при оптимальных коэффициентах ОС мы имеем наилучший баланс между отклонением координат объекта и затрачиваемым управлением.