Стыковочные функции. В-сплайны
У кривых Безье каждая Pi оказывает влияние на кривую для всех значений t от 0 до 1. Желателен же локальный контроль. Решение - множество стыковочных функций, имеющих поддержку только на части интервала [0,1].
|
Данные функции должны: · быть простыми в вычислении; · Sf(t)=1 для любого t из [a,b]; · иметь поддержку лишь на небольшом участке интервала [a,b] для обеспечения локального контроля; · интерполировать определенные контрольные точки; · быть достаточно гладкими. (f(t) – гладкие внутри интервала, начинаются и заканчиваются с нулевым значением производной. |
Рис.1. Локальный контроль |
Кусочно-полиномиальные кривые и сплайны
Поиск кандидатов на роль стыковочных функций.
У кубической формы (вида R(t)= at3+ bt2+ct+d) недостаточно гибкости, чтобы "изогнуться" так, как этого требуется.
Выход – кусочные полиномы (несколько полиномов низкого порядка, различные на различных интервалах t).
Примерная форма кучсочных полиномов g(t), рис.2.
|
· Поддержка кривой g(t) : [0,3], функции определены в диапазонах; · Точки, в которых встречается пара отдельных сегментов – стыки; · Значения t в стыках – узлы; Сплайн-функция M-ой степени – это кусочно-полиномиальная функция степени M, обладающая в каждом узле (M-1) гладкостью. g(t) – пример сплайн-функции – кусочно-полиномиальной функции, обладающей достаточной гладкостью. g(t) – квадратичный сплайн, (непрерывная всюду первая производная). Построение из g(t) множества стыковочных функций gk(t)=g(t-k), где k=0,1,… Сумма gk(t) равна единице (тут выполняется для t в пределах от 2 до 7).
Рис. 3. Стыковочные функции g(t) |
Рис. 2 Примерная форма стыковочной функции g(t) |
Генерация кривой на базе g(t):
V(t)=SPkg(t-k) (t от 2 до 7)
Свойства кривых на базе g(t) функций:
· Некоторый локальный контроль над формой кривой;
· Кривая проходит через середины ребер контрольного полигона;
· Вся кривая 1-гладкая;
· Точки P на кривой не интерполируются;
· Степень полиномов не зависит от числа контрольных точек (любое число точек Pi).
Сплайны и базисные функции
Больший контроль над формой кривой? –> больше "изгибаться" и быть более гладкой кривой.
Общая форма вычисления сплайн кривой:
P(t)=SLk=0PkRk(t)
(L+1) контрольных точек и (L+1) функций R0(t), R1(t)… RL(t).
Последовательность узлов – узловой вектор: T=(t0,t1,t2…) (не убывают).
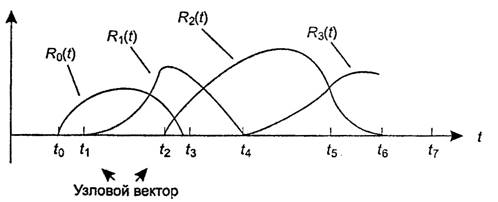
Рис. 4. Узловой вектор
Оющие требования к стыковочным функциям Rk(t):
· Rk(t) – кусочный полиномом, Rk(t)=0 до момента tk,
· Rk(t)¹0 на протяжении нескольких диапазонов вектора T.
· Rk(t) – сплайн-функция, (достаточная степень гладкости).
- Кривая Безье. t Ì 0..1, полиномы Бернштейна – степени (L), (L+1) узел при t=0 и еще (L+1) узел при t=1. Полиномы Бернштейна являются сплайнами, поскольку их производные непрерывны до (L-1)-го порядка включительно.
- Смещения g(t). Узловыми значениями являются целые числа 0,1,…((L+1)+2), каждый компонент g(t-k) является сплайном, 3 полинома 2 степени, активны в диапазоне шириной 3.
Базис сплайнов – некоторое семейство стыковочных функций на заданном узловом векторе, которые можно использовать для генерирования всех возможных сплайн-кривых, определяемых данным узловым вектором.
Существует множество таки семейств. Один особенный базис – B-сплайны ("Basis").
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.