Исследование рекуррентных алгоритмов цифровой фильтрации сигналов методом усреднения. Знакомство с различными алгоритмами цифровой фильтрации сигналов методом усреднения и исследование эффективности их работы в условиях

1.  Цель работы.

Цель работы – знакомство с различными алгоритмами цифровой фильтрации сигналов методом усреднения и исследование эффективности их работы в условиях, когда на полезный сигнал наложена помеха типа «белого шума» с нулевым математическим ожиданием и регулируемой дисперсией.

2.  Методика исследования

Исследуются фильтры на основе следующих алгоритмов:

1) Рекуррентный алгоритм усреднения с бесконечной памятью. Он используется для выделения постоянной составляющей полезного сигнала на фоне помех.

Выражение для него в рекуррентной форме:

При  он обеспечивает .

2) Рекуррентный алгоритм усреднения с постоянным коэффициентом коррекции.

Если принять , то можно записать это уравнение в форме:

Откуда при переходе к непрерывному времени получим передаточную функцию фильтра:

То есть фильтр, построенный по такому алгоритму, при малых значениях  эквивалентен аналоговому низкочастотному фильтру первого порядка.

3) Рекуррентный алгоритм усреднения с конечной памятью.

Эффективность цифровой фильтрации, то есть меру снижения уровня помех на выходе фильтра по сравнению с уровнем помех на входе, будем оценивать следующим образом:

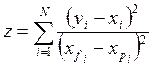
Где:      - зашумленный сигнал на входе фильтра

 - полезный сигнал на входе фильтра

 - сигнал на выходе фильтра

 - полезный сигнал на выходе фильтра

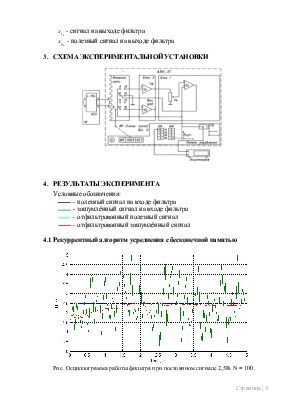
3.  Схема Экспериментальной установки

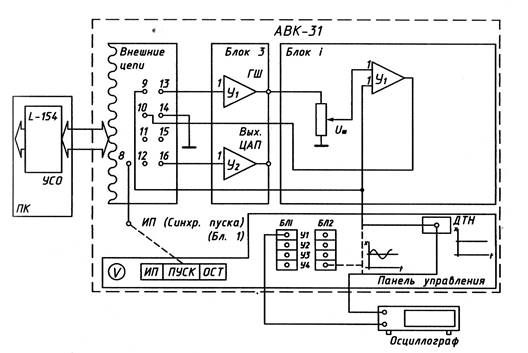
4.  Результаты Эксперимента

Условные обозначения:

- полезный сигнал на входе фильтра

- зашумлённый сигнал на входе фильтра

- отфильтрованный полезный сигнал

- отфильтрованный зашумлённый сигнал

4.1  Рекуррентный алгоритм усреднения с бесконечной памятью

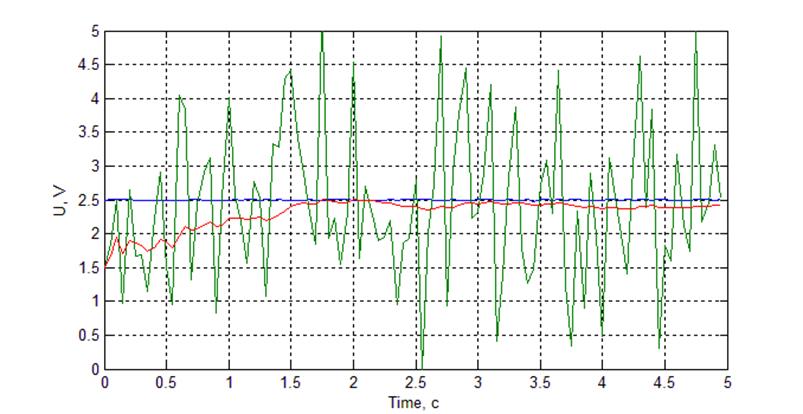
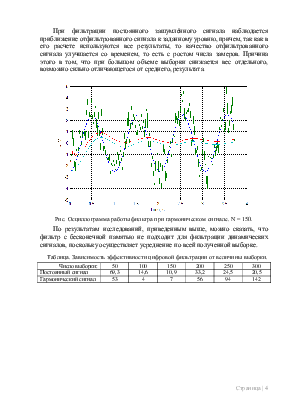
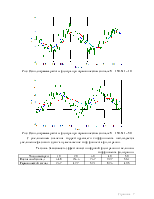
Рис. Осциллограмма работы фильтра при постоянном сигнале 2,5В. N = 100.

При фильтрации постоянного зашумлённого сигнала наблюдается приближение отфильтрованного сигнала к заданному уровню, причем, так как в его расчете используются все результаты, то качество отфильтрованного сигнала улучшается со временем, то есть с ростом числа замеров. Причина этого в том, что при большом объеме выборки снижается вес отдельного, возможно сильно отличающегося от среднего, результата.

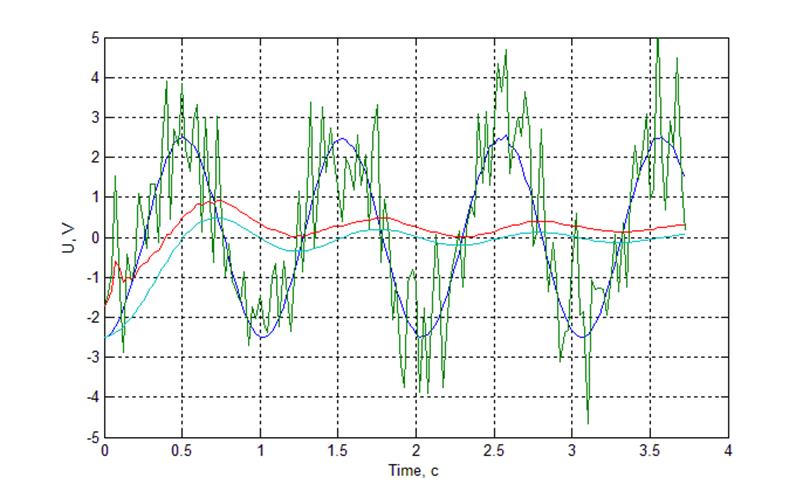
Рис. Осциллограмма работы фильтра при гармоническом сигнале. N = 150.

По результатам исследований, приведенным выше, можно сказать, что фильтр с бесконечной памятью не подходит для фильтрации динамических сигналов, поскольку осуществляет усреднение по всей полученной выборке.

Таблица. Зависимость эффективности цифровой фильтрации от величины выборки.

4.2  Рекуррентный алгоритм усреднения с постоянным коэффициентом коррекции

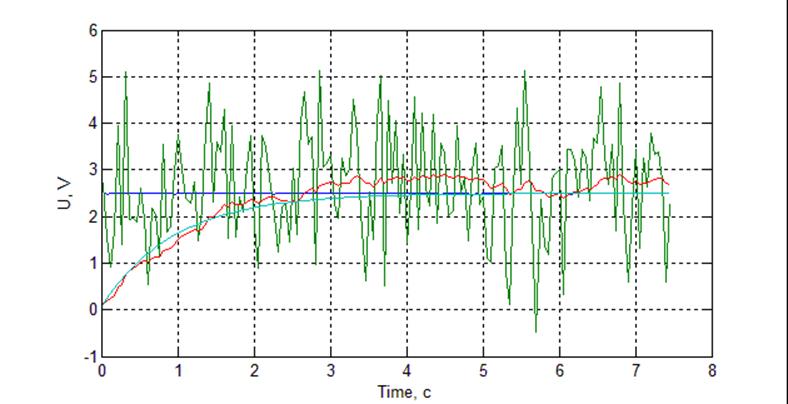
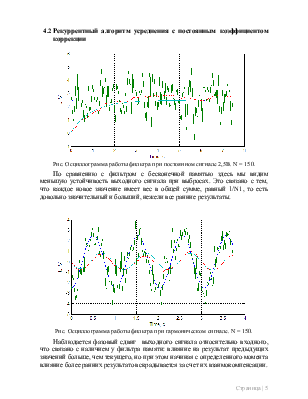
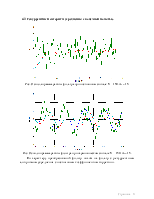
Рис. Осциллограмма работы фильтра при постоянном сигнале 2,5В. N = 150.

По сравнению с фильтром с бесконечной памятью здесь мы видим меньшую устойчивость выходного сигнала при выбросах. Это связано с тем, что каждое новое значение имеет вес в общей сумме, равный 1/N1, то есть довольно значительный и больший, нежели все ранние результаты.

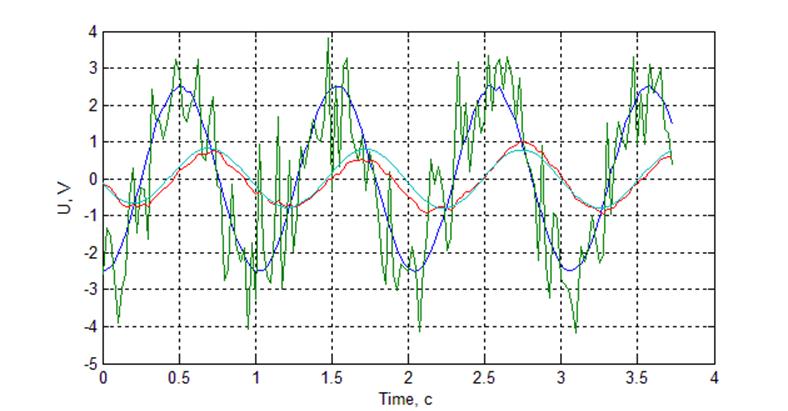
Рис. Осциллограмма работы фильтра при гармоническом сигнале. N = 150.

Наблюдается фазовый сдвиг  выходного сигнала относительно входного, что связано с наличием у фильтра памяти: влияние на результат предыдущих значений больше, чем текущего, но при этом начиная с определенного момента влияние более ранних результатов скрадывается за счет их взаимокомпенсации.

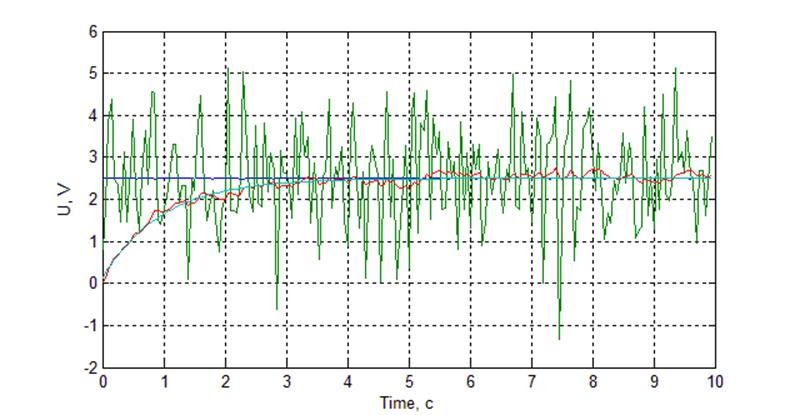
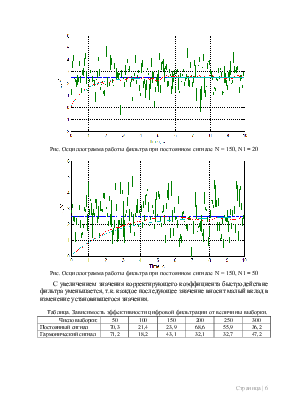
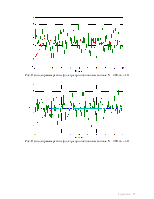
Рис. Осциллограмма работы фильтра при постоянном сигнале N = 150, N1 = 20

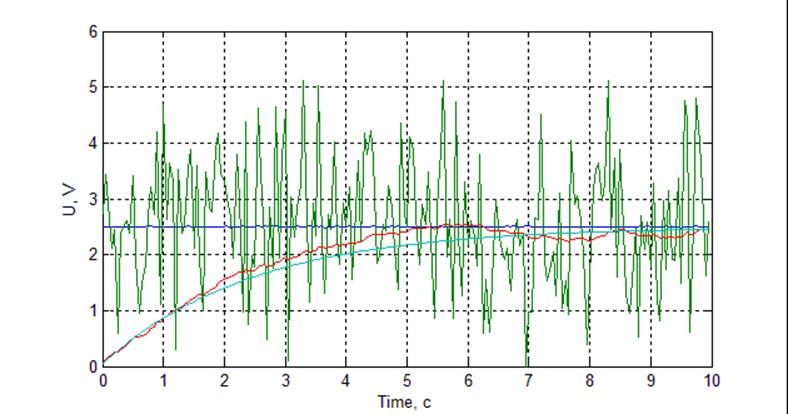
Рис. Осциллограмма работы фильтра при постоянном сигнале N = 150, N1 = 50

С увеличением значения корректирующего коэффициента быстродействие фильтра уменьшается, т.к. каждое последующее значение вносит малый вклад в изменение установившегося значения.

Таблица. Зависимость эффективности цифровой фильтрации от величины выборки.

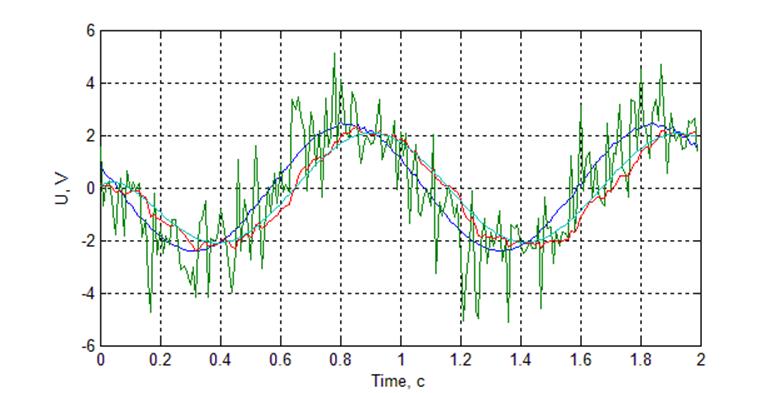
Рис. Осциллограмма работы фильтра при гармоническом сигнале N = 150, N1 = 10

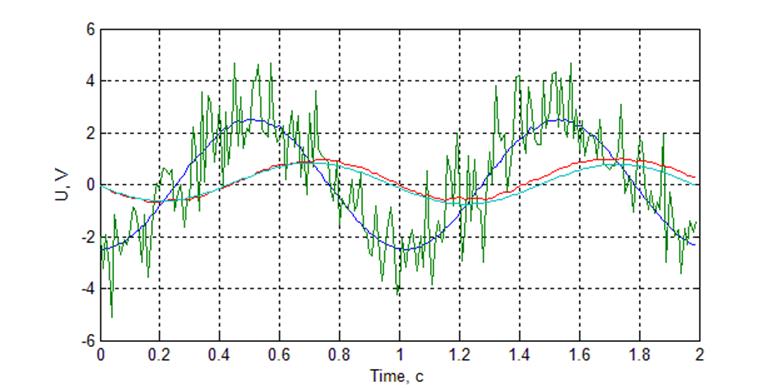
Рис. Осциллограмма работы фильтра при гармоническом сигнале N = 150, N1 = 50

С увеличением значения корректирующего коэффициента наблюдается увеличение фазового сдвига и уменьшение коэффициента фильтрации.

Таблица. Зависимость эффективности цифровой фильтрации от величины коэффициента фильтрации.

4.3  Рекуррентный алгоритм усреднения с конечной памятью

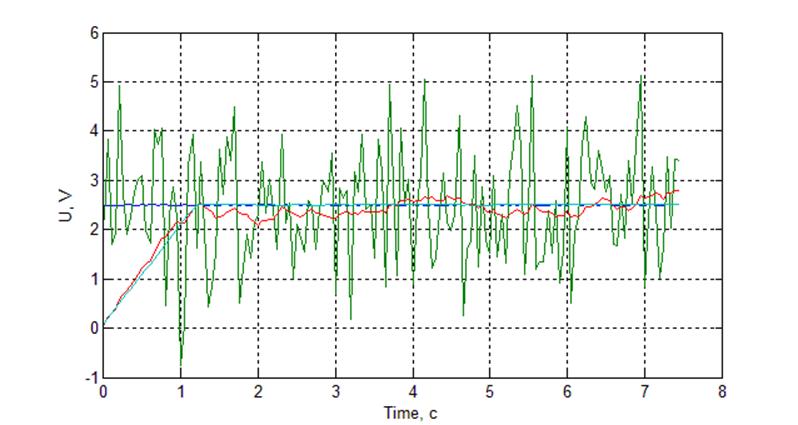
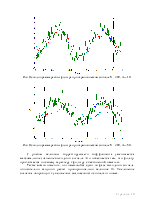
Рис. Осциллограмма работы фильтра при постоянном сигнале N = 150, m = 15.

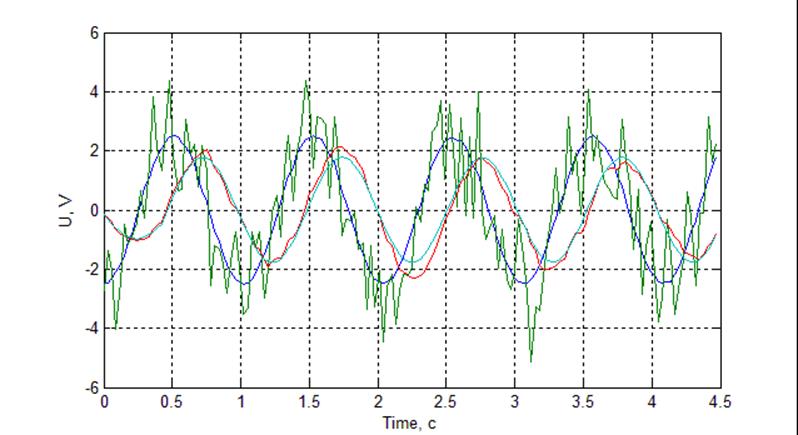
Рис. Осциллограмма работы фильтра при гармоническом сигнале N = 150, m = 15.

По характеру преобразований фильтр похож на фильтр с рекуррентным