Санкт-Петербургский государственный политехнический университет
Кафедра компьютерных систем и программных технологий
Расчётное задание
Дисциплина: Адаптивные системы управления
Тема: Исследование дифференциальной динамики оптимальной системы управления линейным объектом
Выполнил студент группы 5081/1 подпись
Преподаватель С.
подпись
Санкт-Петербург
2011
1. Задание
Задан объект, описываемый линейным дифференциальным уравнением 2-го порядка:
Целевой функционал:
1) Построить линии равного качества вблизи точки оптимума и гиперповерхность критериальной функции.
2) Сравнить процессы в разных точках по интегральному и прямым показателям качества.
3) Исследование влияния на критерий качества и вид переходного процесса дискретности регулятора.
2. Исходные данные
Получим следующее уравнение:
3. Выполнение работы
3.1. Переход к уравнениям состояния
Уравнения состояния и выхода в матричном виде:
.
Получим векторно-матричное уравнение состояния:
3.2. Определение оптимальных коэффициентов обратной связи
Наш многомерный линейный стационарный объект описывается векторно-матричным уравнением вида:
Необходимо синтезировать управление, обеспечивающее перевод объекта из некоторого начального состояния x(t0) = x0 в заданное конечное состояние x(tf) = 0 и минимизацию целевого функционала вида:
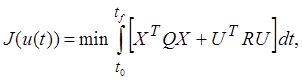
где Q и R – симметричные
неотрицательно определённые диагональные матрицы (Q 
).
В теории управления эта задача известна как линейно-квадратичная (ЛК) проблема оптимального управления.
Её решение позволяет определить параметры обратной связи (регуляторов), обеспечивающей наилучшие процессы в смысле минимального значения функционала.
Решение ЛК-проблемы для стационарных систем может быть получено путём решения алгебраического матричного квадратного уравнения Рикатти вида:
где S – квадратная положительно определённая симметричная матрица.
В результате его решения находится оптимальное значение матрицы S* и матрицы оптимальных коэффициентов ОС:
Оптимальное уравнение формируется в виде:
т. е. в форме пропорциональной обратной связи по всем координатам вектора состояния.
Итак, требуется решить нелинейную векторно-матричную систему вида:
Решение системы можно получить итерационным способом, предварительно преобразовав её к линейной форме.
Для этого помножим второе уравнение слева на R:
Учитывая симметричность матриц S и R, его можно переписать в виде
В результате первое уравнение системы можно преобразовать к виду:
Определим матрицы Q и R, преобразовав 
в 
Отсюда находим 
=> 
Т. к. R – скаляр и S – симметричная матрица, система уравнений примет следующий вид:
Произведём подстановку матриц A, B, S и Q.
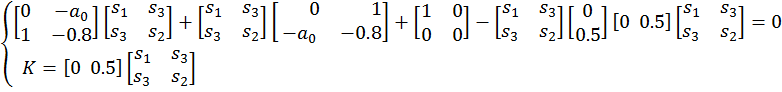
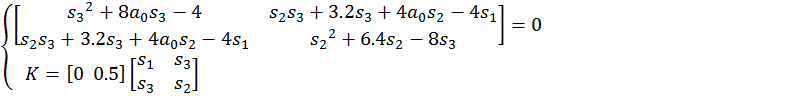
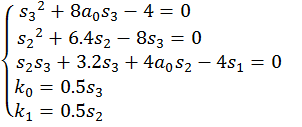
3.3. Построение линий равного качества вблизи оптимума и гиперповерхность критериальной функции
Скрипт в Matlab:
% Формируем ДУ 2 порядка
function out = du(t, params)
a0 = 0.5;
A = [0 1; -a0 -0.8];
B = [0; a0];
k0 = params(4);
k1 = params(5);
U = -k0*params(1) - k1*params(2);
out = zeros(5,1);
out(1:2) = A*params(1:2) + B*U;
out(3) = params(1)^2 + U^2;
out(4:5) = 0;
% Формирование значений матриц
[k0, k1] = meshgrid(0:.1:5);
% Время интегрирования
T = [0 10];
% Начальные условия
X0 = [2; 0];
J0 = 0;
for i=1:length(k0)
for j=1:length(k1)
[t, out] = ode45(@du, T, [X0(1); X0(2); J0; k0(1,i); k1(j,1)]);
J(i, j) = out(end, 3);
end
end
figure
mesh(k0, k1, J)
xlabel('k0')
ylabel('k1')
zlabel('J')
figure
contour(k0, k1, J);
xlabel('k0')
ylabel('k1')
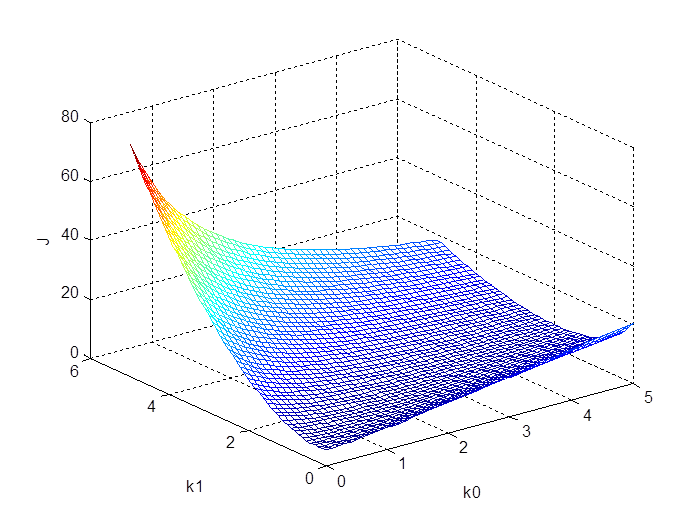
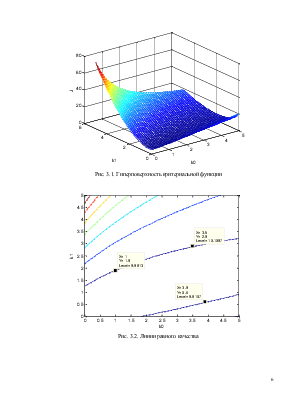
Рис. 3.1. Гиперповерхность критериальной функции
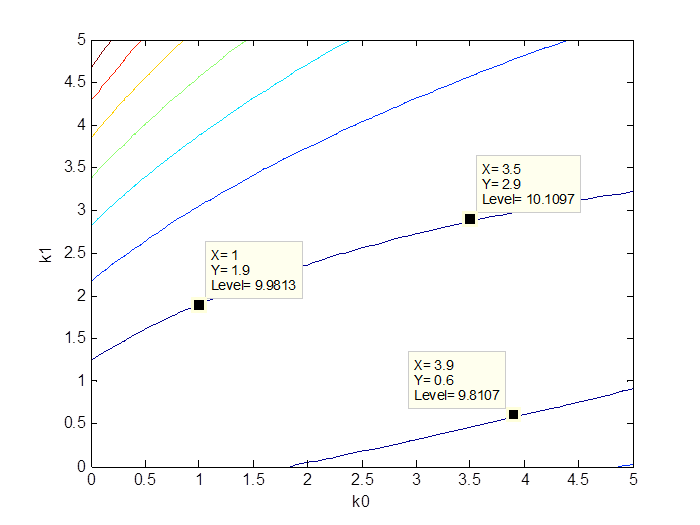
Рис. 3.2. Линии равного качества
3.4. Сравнение процессов в разных точках по интегральному и прямым показателям качества
Выберем одну линию равного качества (J = 10) и несколько пар оптимальных коэффициентов (рис. 3.3).
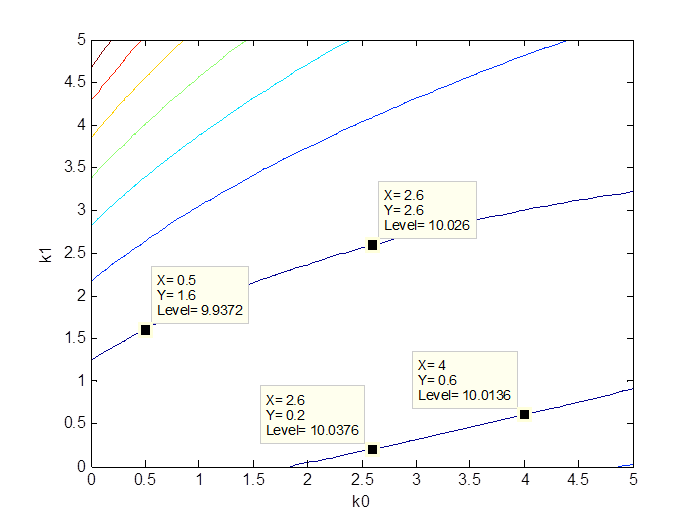
Рис. 3.3. Значения оптимальных коэффициентов для J = 10
Рассмотрим переходные процессы при данных коэффициентах.
На рис. 3.4 представлена схема в Simulink.
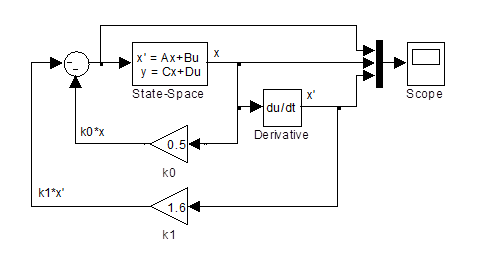
Рис. 3.4. Схема в Simulink
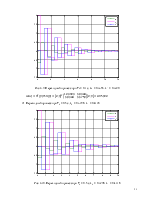
1) Переходный процесс при k0 = 0.5, k1 = 1.6
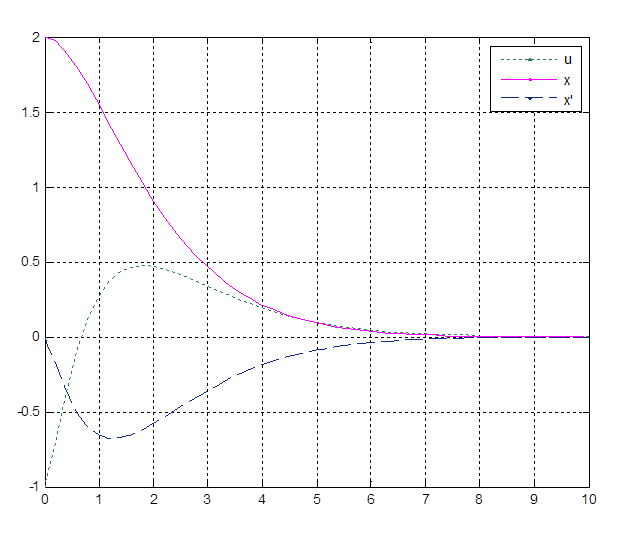
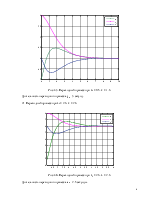
Рис. 3.5. Переходный процесс при k0 = 0.5, k1 = 1.6
Длительность переходного процесса tпп – 5 секунд.
2) Переходный процесс при k0 = 2.6, k1 = 2.6
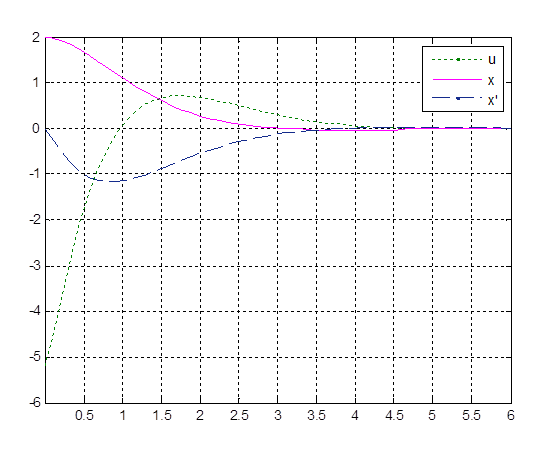
Рис. 3.6. Переходный процесс при k0 = 2.6, k1 = 2.6
Длительность переходного процесса tпп – 2.5 секунды.
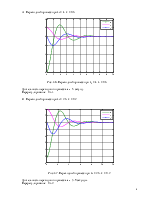
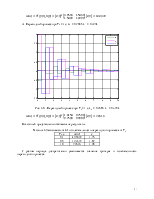
3) Переходный процесс при k0 = 4, k1 = 0.6
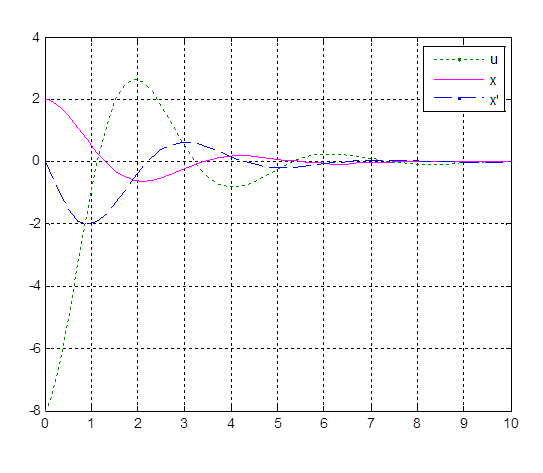Рис. 3.6. Переходный процесс при k0 = 4, k1 = 0.6
Длительность переходного процесса tпп – 5 секунд.
Перерегулирование – 0.31.
4) Переходный процесс при k0 = 2.6, k1 = 0.2
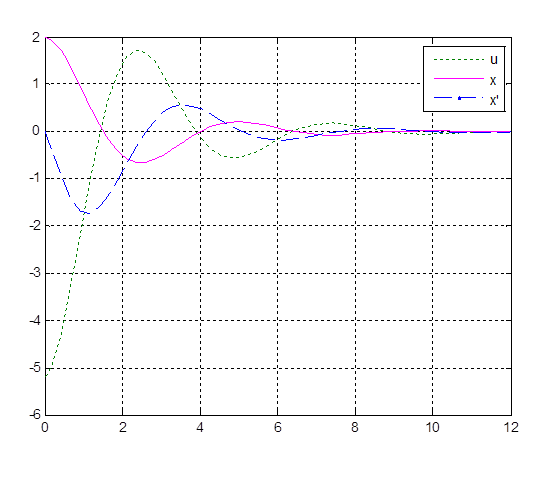
Рис. 3.7. Переходный процесс при k0 = 2.6, k1 = 0.2
Длительность переходного процесса tпп – 5.8 секунды.
Перерегулирование – 0.32.
Из полученных графиков видно, что при равенстве интегрального показателя качества прямые показатели различны. Причём процесс может быть как периодическим, так и апериодическим.
3.5. Исследование влияния на критерий качества и переходный процесс дискретности регулятора
Объект управления описывается линейным векторно-матричным уравнением вида:
Критерий оптимальности:
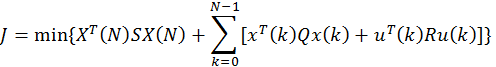
Для каждого из участков траектории можно получить следующие рекуррентные формулы для вычисления оптимальных коэффициентов KN-j, вспомогательной матрицы PN-j, управления u(N-j) и критерия оптимальности JN-j:
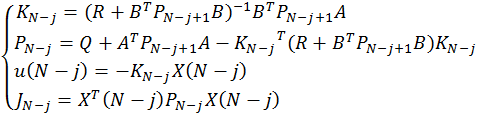
При 
При 
Рассчитаем матрицы 
и 
для
нескольких значений периода дискретизации.
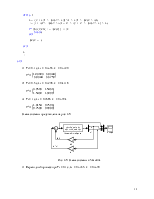
Скрипт в Matlab:
T0 = [0.1 0.5 1];
a0 = 0.5;
A = [0 1; -a0 -0.8];
B = [0; a0];
for i=1:length(T0)
Ad = eye(2);
Bd = eye(2)*T0(i);
for j=1:100
Ad = Ad + A^j*T0(i)^j/factorial(j);
Bd = Bd + A^j*T0(i)^(j+1)/factorial(j+1);
end
T0(i)
Ad
Bd = Bd*B
end
С ростом периода дискретизации уменьшается значение критерия и колебательность переходного процесса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.