Построение и исследование процессов в беспоисковых адаптивных системах прямого типа. Объект задан дифференциальным уравнением второго порядка

Санкт-Петербургский государственный политехнический университет

Кафедра компьютерных систем и программных технологий

Расчетное задание №3

Построение и исследование процессов в беспоисковых адаптивных системах прямого типа

                                  Работу выполнил:

студент гр. 5081/10

Работу проверил:

преподаватель

Санкт-Петербург

2012

1.  Постановка задачи

Объект задан дифференциальным уравнением второго порядка.

В работе производится построение и исследование процессов в беспоисковых адаптивных системах прямого типа.

2.  Программа работы

Требуется:

1)  Построить эталонную модель;

2)  Исследовать процессы во вторичном контуре при интегральных билинейных законах настройки;

3)  Провести модификацию исходных законов для улучшения процесса настройки.

3.  Вариант задания

При исследовании использовался тот же объект, что и в предыдущих расчетных заданиях. Математическая модель объекта описывается следующим образом:

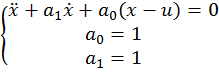
4.  Подготовка к выполнению работы

Беспоисковые адаптивные системы с эталонной моделью (БАСЭМ) нужны для ликвидации разности выходов основного контура и эталонной модели, т.е. для ликвидации координатной ошибки. БАСЭМ представляют собой наиболее важный класс, т.к. для него все доказано наиболее строго.

Достоинства подхода:

·  Формирование алгоритма адаптации происходит на основе легко доступных измеряемых величин, что определяет быстроту реакции.

·  Не нужны дополнительные пробные движения.

Структура БАСЭМ представлена на рисунке 4.1.

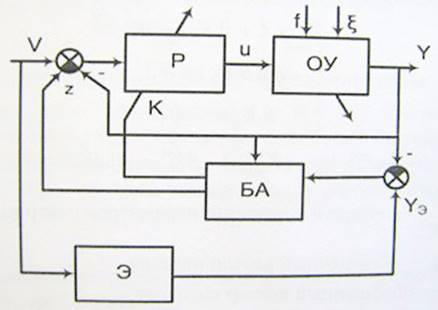
Рис. 4.1. Структура БАСЭМ

В качестве беспоискового алгоритма будем использовать метод скоростного градиента.

В этом алгоритме изменение настраиваемых параметров производится в направлении, противоположном градиенту скорости изменения  функционала, характеризующего качество оптимизации.

P = P^T > 0;

- основная функция качества;

P - симметричная и положительно определенная диагональная матрица;

Цель: при,

Скорость:

где: e – координатная ошибка основного контура по сравнению с эталоном

А_Э – матрица эталонного поведения системы

B – матрица управления системы

Р – обобщенный вектор сигналов

Целевая функция:

Отсюда получим закон изменения параметров регулятора:

Запишем уравнение регулятора как:

В этом случае можно записать следующие выражения для коррекции его коэффициентов:

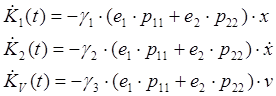
где:  - диагональные элементы матрицы Г

 - ошибка по

 - ошибка по

5.  Результаты исследований

5.1.Исходная система

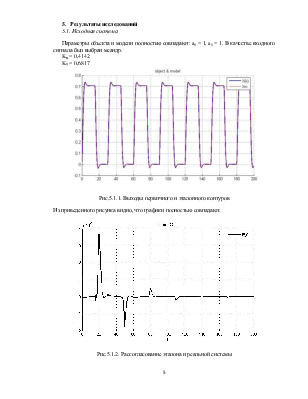
Параметры объекта и модели полностью совпадают: a₀ = 1, a₁ = 1. В качестве входного сигнала был выбран меандр.

K_п = 0,4142

K_д = 0,6817

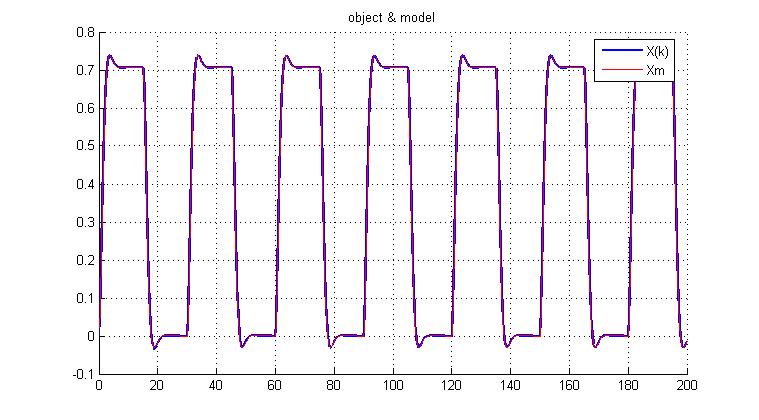
Рис.5.1.1. Выходы первичного и эталонного контуров

Из приведенного рисунка видно, что графики полностью совпадают.

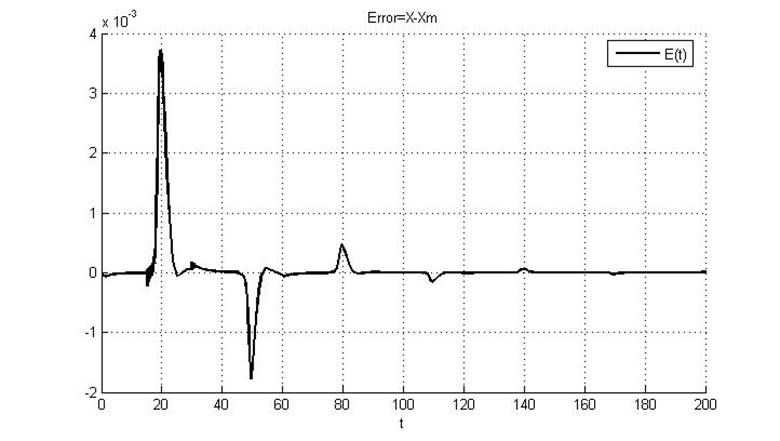
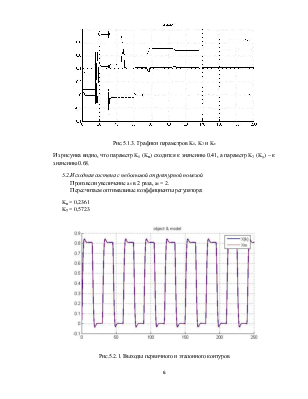
Рис.5.1.2. Рассогласование эталона и реальной системы

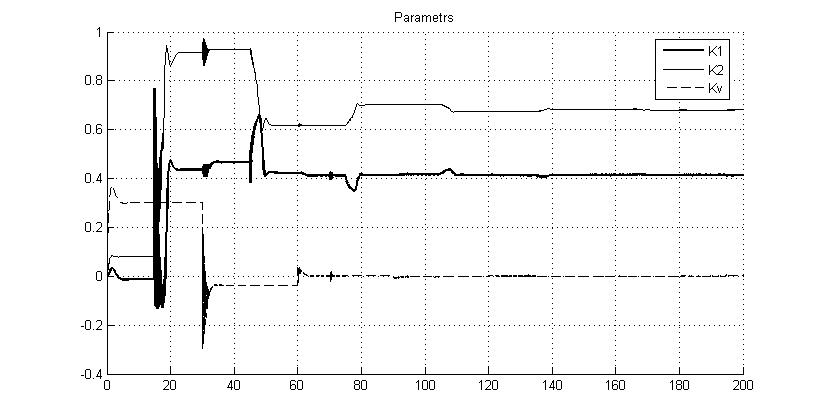
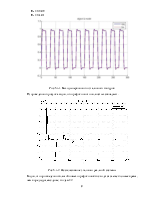
Рис.5.1.3. Графики параметров K₁, K₂ и K_v

Из рисунка видно, что параметр K₁ (K_п) сходится к значению 0.41, а параметр K₂ (K_д) – к значению 0.68.

5.2.Исходная система с небольшой структурной помехой

Произвели увеличение a₀ в 2 раза, a₀ = 2.

Пересчитаем оптимальные коэффициенты регулятора:

K_п = 0,2361

K_д = 0,5723

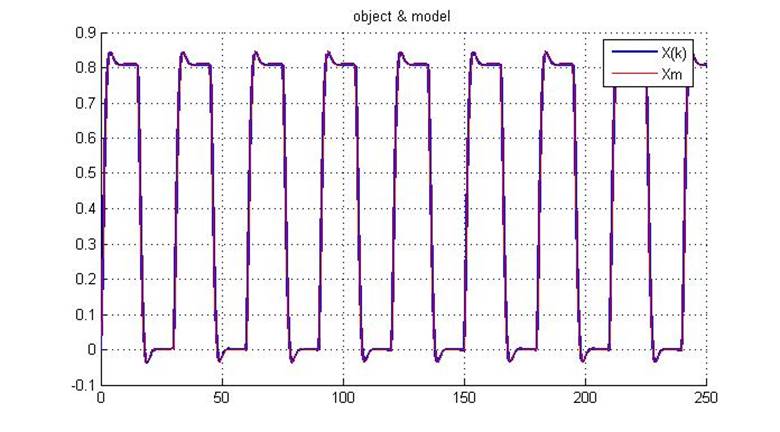
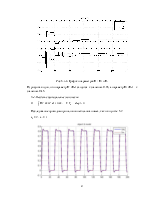
Рис.5.2.1. Выходы первичного и эталонного контуров

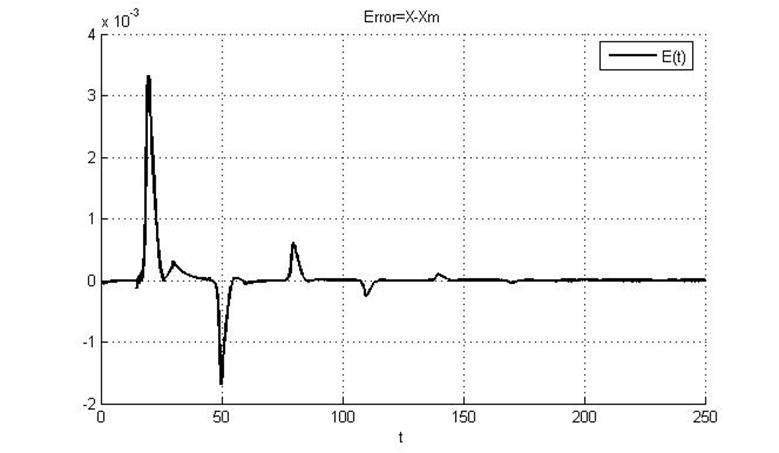
Рис.5.2.2. Рассогласование эталона и реальной системы

Видно, что при введении небольшой помехи график ошибки сходится за большее время.

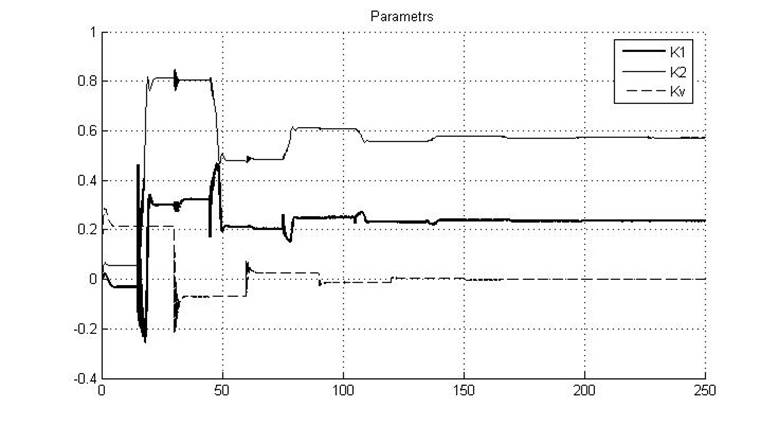
Рис.5.2.3. Графики параметров K₁, K₂ и K_v

Из рисунка видно, что параметр K₁ (K_п) сходится к значению 0.23, а параметр K₂ (K_д) – к значению 0.57.

5.3.Исходная система с большой структурной помехой

Произвели увеличение a₀ в 10 раза, a₀ = 10.

Пересчитаем оптимальные коэффициенты регулятора:

K_п = 0,0499

K_д = 0,4491

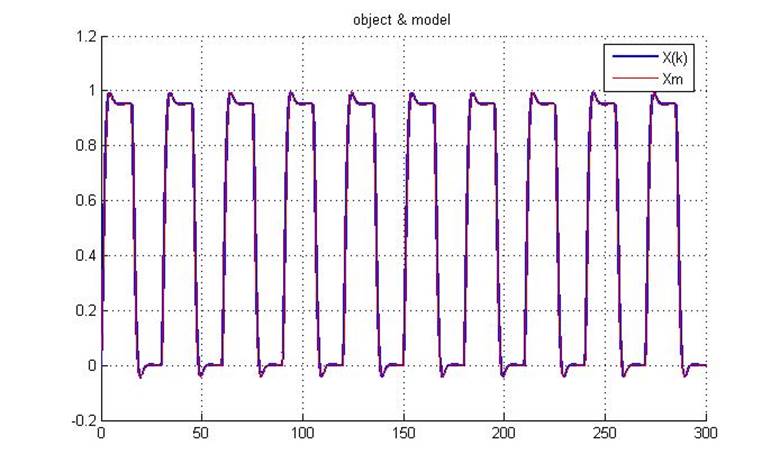
Рис.5.3.1. Выходы первичного и эталонного контуров

Из приведенного рисунка видно, что графики почти полностью совпадают.

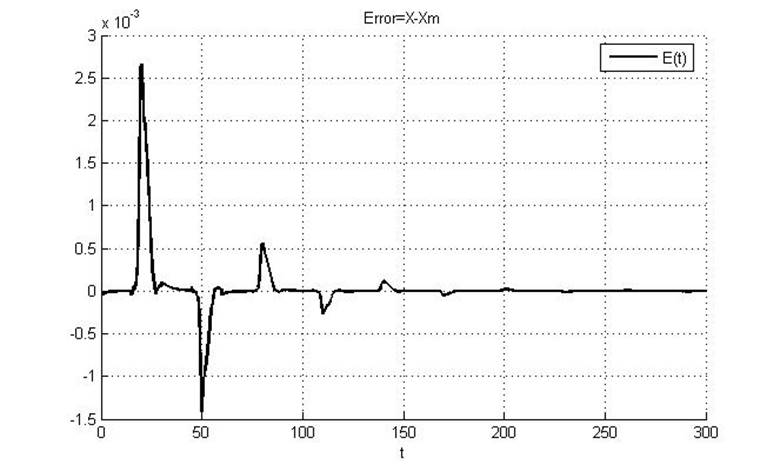
Рис.5.3.2. Рассогласование эталона и реальной системы

Видно, что при введении большой помехи график ошибки сходится за еще большее время, чем в предыдущем случае, когда a₀=2.

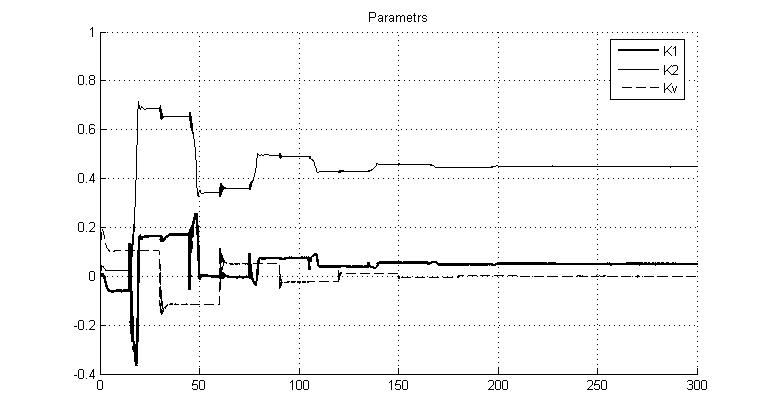
Рис.5.3.3. Графики параметров K₁, K₂ и K_v

Из рисунка видно, что параметр K₁ (K_п) сходится к значению 0.05, а параметр K₂ (K_д) – к значению 0.45.

5.4. Введение пропорционального члена

Исследование проводим при наличии небольших помех, как и в пункте 5.2

a₀ = 2,   a₁ = 1

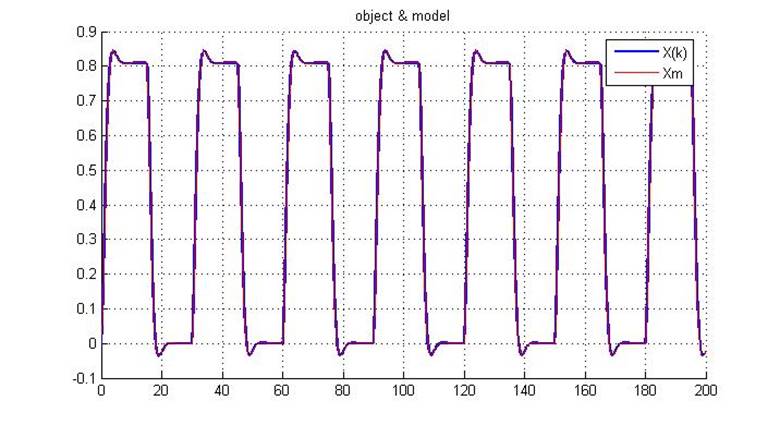
Рис.5.4.1. Выходы первичного и эталонного контуров

Как видно из рисунка, графики полностью совпадают.

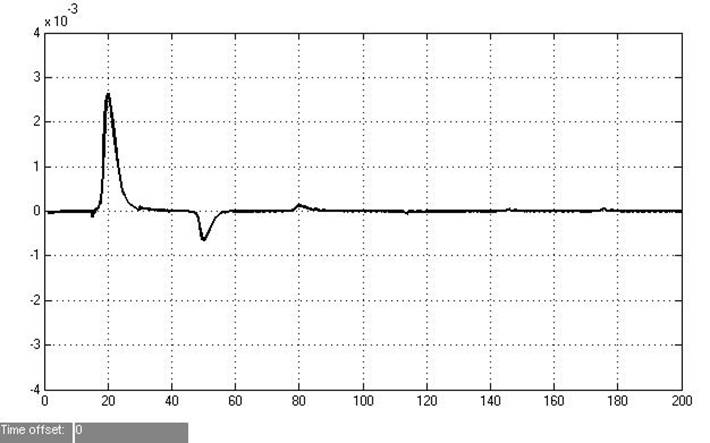
Рис.5.4.2. Рассогласование эталона и реальной системы

После введения пропорциональной составляющей величина ошибки уменьшилась и график стал сходится к 0 гораздо быстрее (100 с.)

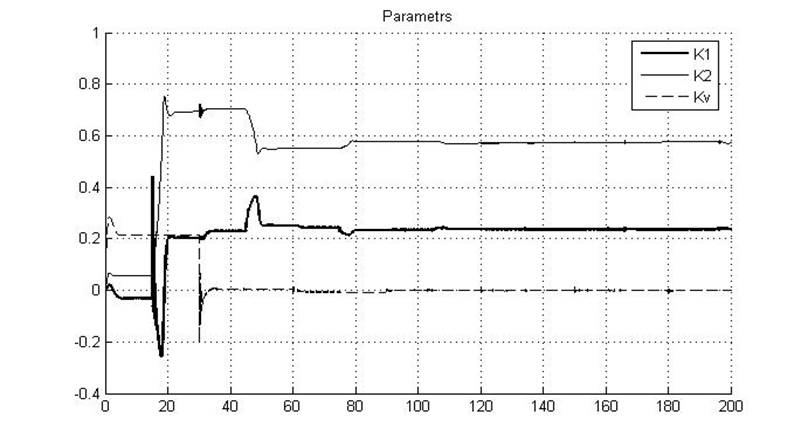
Рис.5.4.3. Графики параметров K₁, K₂ и K_v

Из рисунка видно, что параметр K₁ (K_п) сходится к значению 0.23, а параметр K₂ (K_д) – к значению 0.57.

5.5 Добавление дифференциального члена

Как и в пункте 5.2 исследование будем производить при при наличии структурной помехи, т.е. a₀ = 2.

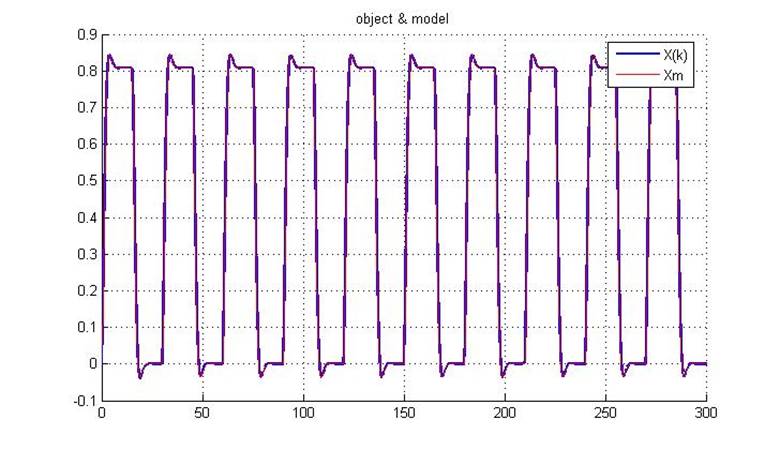
Рис.5.5.1. Выходы первичного и эталонного контуров

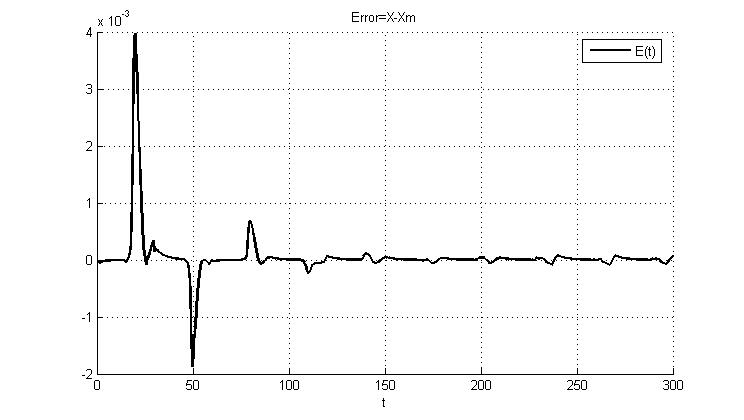
Рис.5.5.2. Рассогласование эталона и реальной системы

После введения дифференциальной составляющей усилилось влияние помех, значение выбросов ошибки увеличилось. Эти небольшие выбросы заметны и после 300 с. Однако, сходимость ошибки, по сравнению с п.5.2 улучшилась.

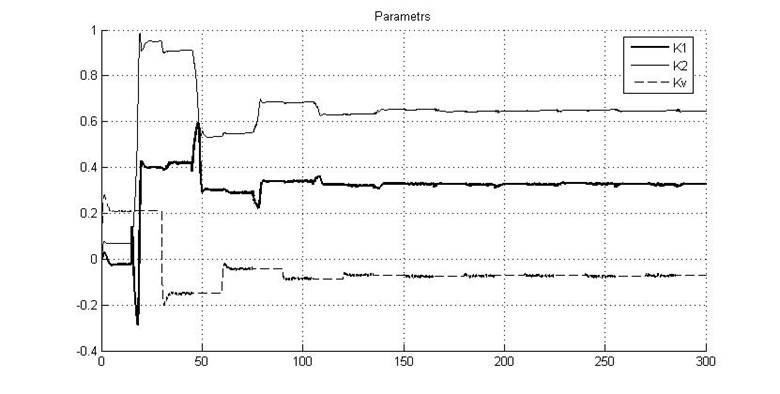
Рис.5.5.3. Графики параметров K₁, K₂ и K_v

Из рисунка видно, что параметр K₁ (K_п) сходится к значению 0.34, а параметр K₂ (K_д) – к значению 0.63.

6.  Выводы

В ходе выполнения данной работы была исследована беспоисковая адаптивная система с эталонной моделью, построенная на основе метода скоростного градиента. Можно утверждать, что система оказалась работоспособной, т.к. во время работы она производит коррекцию коэффициентов регулятора и подстройку выходов основного контура относительно эталонного, что можно наблюдать на примере затухающего характера ошибки по x.

При введении даже структурных помех ошибка по x и время подстройки увеличивались.

Введение в систему пропорционального члена приводит к значительному уменьшению величины колебаний ошибки и, как видно из графика, уменьшению времени подстройки.

При введении дифференциального члена наблюдается увеличение быстродействия системы, но усиливается влияние даже малых по величине помех.