Совершенствование тяговых электрических машин на автономных локомотивах. Электрические передачи мощности тепловозов с асинхронными двигателями

Если прямой расчет упругой характеристики резинового элемента простейшей формы с некоторыми допущениями еще возможен, то демпфирующее действие непосредственно рассчитать нельзя. В этом случае расчетные данные контролируются путем измерений, результаты которых затем используются и качестве основы для моделирования.

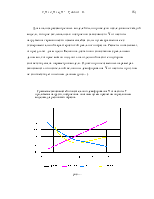
Если к резиновому амортизатору прикладывают статическую и динамическую нагрузки с постоянной амплитудой и частотой на установке для испытаний на растяжение и сжатие с пульсирующим воздействием, то по результатам снятия характеристики сила-прогиб для одного цикла нагружения можно построить кривую гистерезиса. 

Жесткость амортизатора определяется из уравнения     

Для оценки демпфирования может быть использована относительная величена демпфирования. Данная величена представляет собой численное значение отношения совершенной в течении цикла работы демпфирования Адемпф (работа потерь) к потенциальной энергии Аакком (работа накопления) и находится из кривой гистерезиса :

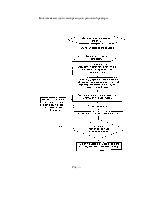
С помощью данных характеристик можно определить наиболее важные для динамических процессов свойства резиновых амортизаторов. На основании этого разработана схема расчетно-экспериментального метода определения параметров математической модели резинового амортизатора, представленная на рис.N. Для проведения испытаний был использован испытательный стенд типа ЦД-100 предприятия   “ Werkstoffprufmaschinen”.Стенд позволяет реализовать относительно небольшой диапазон получаемых частот (от 2 до 10 Гц). В качестве резинового образца был изготовлен фрагмент резиновой рессоры, предлагаемой к установке на новую конструкцию тележки для грузовых вагонов повышенно грузоподъемности. Рессора имела пластинчатую форму толщиной 20 мм с продольными прорезями для компенсации формоизменения при деформации.

Для проведения испытаний был выбран режим, при котором к образцу прикладывалась нагрузка в диапазоне от 2 до 4 тс . После того, как стенд выходил на режим постоянной частоты, регистрировались величена нагрузки, действующей на образец и перемещения образца под нагрузкой. По данным значениям строились кривые гистерезиса. Полученные экспериментальные данные, согласно алгоритму на рис.N служат основой для выбора математической модели поведения резиновой рессоры под периодической нагрузкой.

Блок-схема методики выбора модели резиновой рессоры.

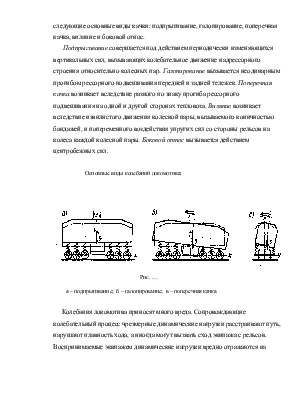
Рис. …

В процессе разработки математической модели использовались простейшие реологические модели Максвелла и Кельвина. Для оптимального выбора модели и анализа свойств рессоры разрабатывались три условия для каждой модели:

1)  безынерционная  модель с внешней  вынуждающей периодической силой;

2)  инерционная модель (без внешней вынуждающей периодической силы);

3)  инерционная модель с внешней вынуждающей периодической силой;

В модели Кельвина резиновый амортизатор представлен в виде параллельно включенных пружин и демпфер, не имеющих массы (рис…). Для определения перемещений точки А в системе составлено уравнение, характеризующее состояние системы. Так как система безинерционная, то все уравнения сводятся к одному уравнению кинетостатики:

        Безинерционная модель Кельвина с внешней вынуждающей силой.

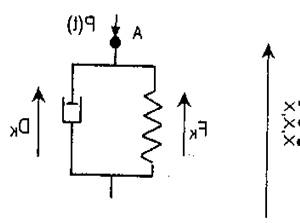
Рис…

, или с учетом представления сил и того, что Р(t)=P*sin(t), получим:

,                                                            (1)

где - круговая частота воздействия внешней вынуждающей силой;

- жесткость пружины в модели Кельвина; X- перемещение в системе;

- коэффициент демпфирования в гасителе модели Кельвина.

Для решения уравнения используется численный метод. Решение для 

i+1 временного слоя находится из уравнения (1), аппроксимированного разностной схемой по формуле

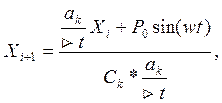                                                              (2)

где - шаг интегрирования.

Модель Максвелла в безинерционном варианте состоит из последовательно соединенных пружины и демпфера, не имеющих массы (рис…). В модели Максвелла сохраняется основной закон механик- действие равно