Ортогональные сигналы. Скалярное произведение сигналов. Ортогональные сигналы и обобщенные ряды Фурье

Лекция 3

Ортогональные сигналы

1. Скалярное произведение сигналов.

2. Ортогональные сигналы и обобщенные ряды Фурье.

3. Примеры ортонормированных базисов.

4. Энергия сигнала, представленная в виде обобщенного ряда Фурье.

5.Апаратурная реализация разложения сигнала по ортонормированному базису.

Рассмотрев структуру ЛПС, определив норму и метрику, мы пока лишены возможности вычислить угол между векторами, это удается при введении скалярного произведения сигналов.

c=(a,b)=|a|*|b|cosφ

1. Если в обычном декартовом пространстве известны два вектора, то:

                                                                        (1)

По аналогии вычислим энергию суммы двух сигналов U и V:

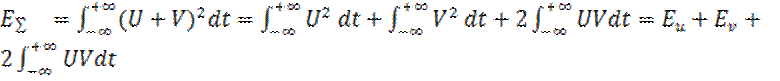                                                                                                         (2)

Сигналы U и V аддитивны, а их энергии нет. Энергия суммарного сигнала содержит в себе некую взаимную энергию:

Сравнивая (2) и (1) определяем скалярное произведение сигналов U и V:

                                                                                     (3)

а также                                                                                     (4)

Свойства скалярного произведения сигналов (5):

1) (U,V)≥0.

2) (U,V)=(V,U).

3) (λU,V)=λ(U,V), λ – вещественное число.

4) (U+V,W)=(U,W)+(W,V).

ЛПС в котором введено скалярное произведение (3), при этом условия (5) – справедливы, то оно называется вещественным гильбертовым пространством H.

В гильбертовом пространстве справедливо неравенство Коши-Буняковского:

|(U,V)|≤||U||*||V||                                                                                                     (6)

Для комплексного гильбертового пространства скалярное произведение:

                                                                                     (7)

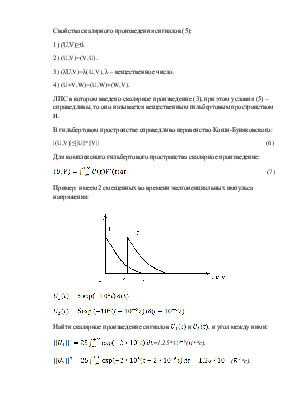
Пример: имеем 2 смещенных во времени экспоненциальных импульса напряжения:

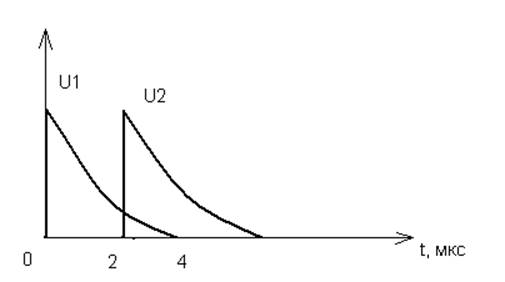
Найти скалярное произведение сигналов  и , и угол между ними:

=1.25*(*c).

(*c).

(*c).

2. Два сигнала U, V – ортогональны, если их скалярное произведение и взаимная энергия равны нулю.

                                                                              (8)

То есть ортогональные сигналы предельно не похожи друг на друга.

Ортонормированный базис.

Пусть H – это гильбертовое пространство сигналов (ГПС) с конечным значением энергии. Эти сигналы определены на промежутке [t1, t2], конечном или бесконечном. Пусть на этом же интервале определена бесконечная система функций {U1, U2, …, Un, …} попарно ортогональных друг другу, обладающих единичными нормами. Это означает, что

                                                                                                 (9)

Следовательно, говорят, что при этом в ГПС задан ортонормированный базис.

Произвольный сигнал S(t), пренадлежащий H, можно разложить в следующий ряд:

                                                                                (10)

Получили обобщенный ряд Фурье.

Отыщем коэффициент  ряда (10): C1, C2, …:

возьмем базисную функцию φ_k. Умножим на нее обе части (10) и проинтегрируем обе части по заданному интервалу [t1, t2].

                                                                (11)

В следствии ортонормированности базиса правая часть (11) равняется Ck.

                                                                         (12)

Из формулы (12) следует алгоритм вычисления коэффициентов C1, C2, … обобщенного ряда Фурье (ОРФ).

Представления сигналов ОРФ освобождает нас от необходимости изучать функциональную зависимость в несчетном множестве точек и дает право характеризовать эти  сигналы коэффициентами C1, C2, …, которые являются проекциями вектора S(t) на базисные направления ГПС.

3. а) ортонормированная система гармонических сигналов на интервале [0,T] (13):

…

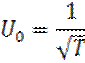
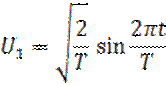
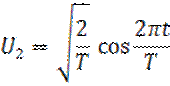
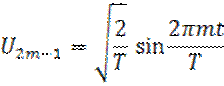
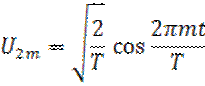
Разложение периодической функции в ряды Фурье по этой ортонормированной системе будет рассмотрено далее.

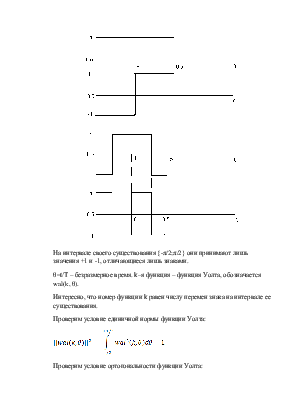
б) система функций Уолта.

Эта система, графики которой на рисунке 1, являются ортонормированными:

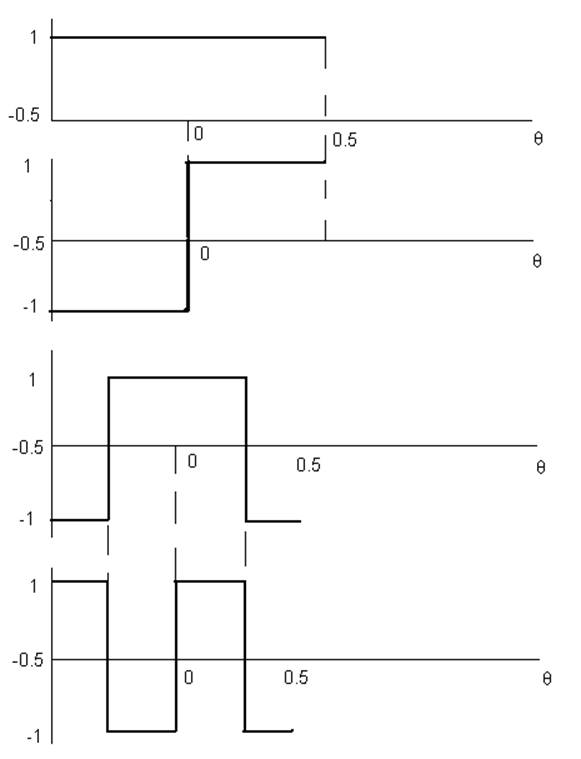
На интервале своего существования {-π/2;π/2} они принимают лишь значения +1 и -1, отличающиеся лишь знаками.

θ=t/T – безразмерное время. k–я функция – функция Уолта, обозначается wal(k, θ).

Интересно, что номер функции k равен числу перемен знака на интервале ее существования.

Проверим условие единичной нормы функции Уолта:

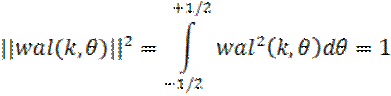
Проверим условие ортогональности функции Уолта:

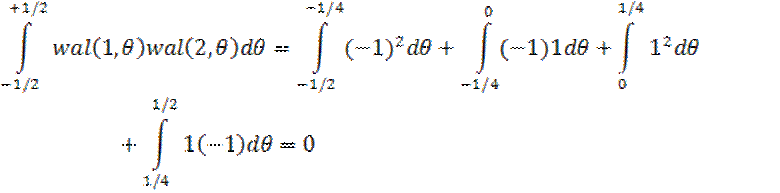
Сигнал с конечной энергией, заданный на интервале (-Т/2; Т/2), можетбыть разложен в обобщенный ряд Фурье по функции Уолта так:

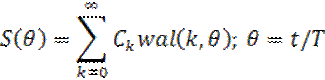                                                                      (14)

4. Пусть сигнал s(t) разложен в обобщенный ряд Фурье:

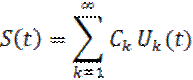
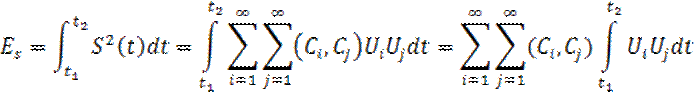         (15)

Поскольку базисная система ортонормированная, то в формуле (15) отличаются от нуля члены с i=j.

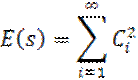                                                                                                        (16)

Следовательно, энергия сигнала равна сумме энергий всех компонент из которых складывается обобщенный ряд Фурье.

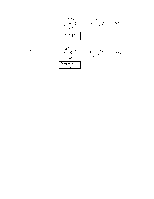
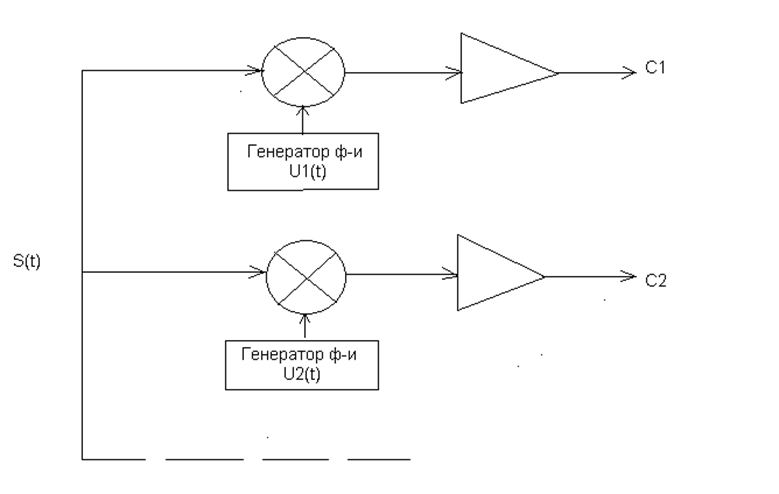
5. Схема, изображенная на рисунке, реализует алгоритм вычисления коэффициентов обобщенного ряда Фурье по формуле (12).

Ck появляется на выходе интеграторов в виде неизменного во времени сигнала в концне промежутка времени интегрирования.