Оптимальный прием сигналов. Показатели качества приема сигнала. Критерии оптимальности приема сигналов

Лекция 14-15

Оптимальный прием сигналов

1) Показатели качества приема сигнала.

2)Критерии оптимальности приема сигналов.

3) Алгоритм оптимального приема (ОП).

4) Статистика принятого сигнала.

1. Задачи приема решаются при двух взаимоисключающих условиях:

A₀ – сигнала нет.

A₁ – сигнал есть.

Эти условия обычно неизвестны или заданы априорными вероятностями: P(A₀) и P(A₁), для которых P(A₀)+P(A₁)=1.

Наличие помех и флюктуаций сигнала приводит к возможности принятия ошибочных решений: ведь при каждом условии A₀ и A₁ могут быть приняты 2 оценочных решения .

Вероятности этих событий:

, , ,  – дают полную характеристику качества приема.

Поскольку условие  и решение  - зависимые события, то каждая из этих вероятностей может быть определена по такой формуле:

                                                                                           (1)

 - априорная вероятность.

 - условная вероятность.

Априорные вероятности  и  практически всегда неизвестны, поэтому за показатели качества обнаружения принимают следующие условные вероятности решений (2):

 - правильное обнаружение.

 - ложная тревога.

 – вероятность пропуска.

 - правильное необнаружение.

Вероятности, соответствующие одному условию, связаны такими соотношениями:

                                                                                                             (3)

Показателями качества обнаружения может быть любая из пар:

D, F; D, ; , F;  .

D – условная вероятность правильного обнаружения.

F – условная вероятность ложной тревоги.

2. Критерии ОП – правило, по которому из всех возможных приемников выбираем наилучший.

Наиболее известный критерий Байеса (критерий минимума среднего риска).

Оптимальный такой приемник, который имеет минимальную вероятность ошибочных решений, учитывая их вес или степень нежелательности.

Оптимизация по критерию Байеса:

1) Каждому ошибочному решению (пропуск сигнала или ложная тревога) ставится в соответствие некоторый вес или стоимость: .

2) Определяется средний риск – средняя стоимость ошибочных решений:

                                                                      (4)

3) Производится определение правила обработки принятого сигнала, при котором минимизируется средний риск. В (4) подставим (1) с учетом (2) и (3):

Вынесем за скобки :

                                                                                (5)

 - весовой множитель                                                                        (6)

, если                                                                              (7)

Условие (7) характеризует оптимальный приемник. Сравнивая последний с любым неоптимальным, можно записать, что:

                                                                          (8)

Из (8) следует основное свойство оптимального приемника: он обеспечивает наибольшую условную вероятность правильного обнаружения D среди всех обнаружителей, у которых .

3. Принятый сигнал y(t) отличается от передаваемого сигнала x(t) тем, что к нему на входе приемника примешивается помеха n(t):

y(t) = A x(t) + n(t)                                                                                                   (9)

A=1, если сигнал есть (A₁).

A=0, если сигнала нет (A₀).

Задача приема: все множество возможных значений принимаемого сигнала y(t) надо разбить на 2 непересекающиеся подмножества Y₀ и Y₁ и если принятая реализация y(t) попадает в Y₀, то A₀, а если в Y₁, то A₁ (сигнал есть). При этом Y1 называется областью принятия решения.

Каждая реализация случайного процесса (СП) y(t) полностью характеризуется плотностями вероятности:

 - плотность вероятности “сигнал + помеха”.

 - плотность вероятности помехи.

Эти плотности считаются заданными и позволяют определить искомые показатели приема сигнала.

                                                                                               (10)

                                                                                                 (11)

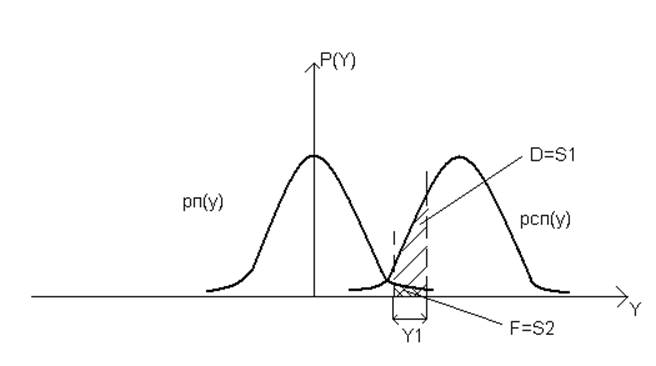
Рисунок 1

Для нахождения правила оптимального приема (выбора оптимальной области решений [Y_1опт]) надо в (10) и (11) подставить основное условие критерия (7) и решить его, получим (12):

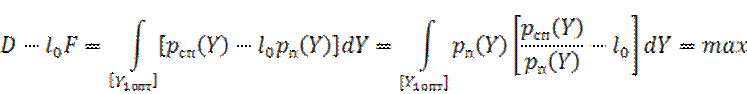
Интеграл в (12) принимает максимальное значение, если подинтегральное выражение положительно.

                                                                           (13)

Левая часть (13) называется отношением правдоподобия:

                                                                            (14)

Отсюда правило оптимального приема:

оптимальный по критерию минимального среднего риска приемник должен по принятой реализации входного сигнала Y вычислять отношение правдоподобия l(Y) и сравнивать его с порогом . В случае если , то сигнал есть, а если , то сигнала нет.

Отношение правдоподобия l(Y) показывает во сколько раз условная вероятность приема реализации Y, при наличии полезного сигнала отличается от условной вероятности той же реализации при отсутствии сигнала (рисунок 2). Чем больше амплитуда сигнала, тем больше l(Y).

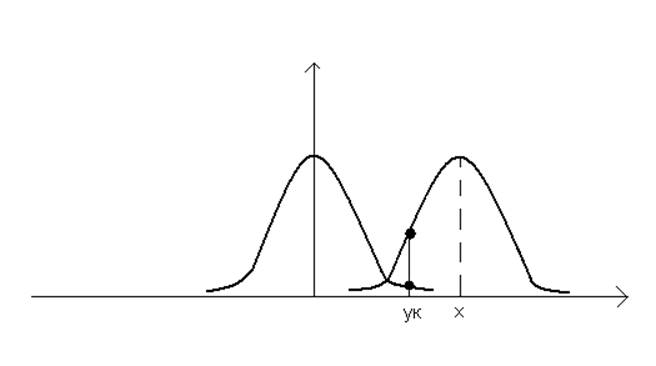
Рисунок 2

Величина l(y_k) является случайной, так как соответствует отношению двух функций от СВ.