Оптимальный прием сигналов. Показатели качества приема сигнала. Критерии оптимальности приема сигналов, страница 2

Для реализации сигнал l(Y) описывается весьма сложным выражением. С целью упрощения структуры обнаружителя можно вместо l(Y) вычислять монотонно связанную с ней функцию, зависящую от Y и сравнивать с соответствующим этой функции порогом. Такая функция называется достаточной статистикой λ(Y).

Она определяется путем перехода l(Y) в lnl(Y) и тогда λ(Y) есть информационная часть lnl(Y).

Правило ОП может быть записано в следующих вариантах (15):

l(Y)> или λ(Y)> (при )

l(Y)< или λ(Y)< (при )

Величина порога  (формула (6)) . Это требует знания стоимости ошибочных , , , . И вместо общего критерия Байеса используют частные.

Наибольшее применение находит критерий Неймана-Пирсона. По этому критерию фиксируется условная вероятность ложной тревоги F  и максимизируется условная вероятность D:                   (16)

Основное преимущество:

порог принятия решения  определяется как функция F и не требует знания стоимости , , , : .

Правило обнаружения позволяет сформулировать методику синтеза оптимального приемника:

1) Изучение статистики принятого сигнала y(t) и получение выражений для  и .

2) Вычисление l(Y) и определение λ(Y).

3) Подбор физических реализуемых элементов, позволяющих вычислить l(Y) и λ(Y)

4) Составление структурой схемы приемника.

5) Оценка показателя качества приема D, F.

4. Рассмотрим статистику принятого сигнала при двух случаях:

1) y(t)=n(y) – флюктуационная помеха.

2) y(t)=n(t)+x(t, α, β) – на входе сигнал + помеха.

α – совокупность полезных параметров.

β – совокупность случайных не измеряемых параметров.

а) Флюктуационная помеха (ФП). Теорема Котельникова.

ФП – внутренние шумы приемника ТКС или внешние шумовые помехи.

ФП представляет собой ССП, обладающий свойством эргодичности с нормальным законом распределения мгновенного значения и нулевым математическим ожиданием.

Одномерная ПВ y(t)=n(t) определяется выражением:

                                                                                    (17)

 - дисперсия ФП.

С целью упрощения анализа используют две модели ФП: КБШ (квази белый шум) и БШ.

КБШ.

КБШ – шум, имеющий постоянную спектральную плотность N₀ от 0 до f_max≈10¹³ГЦ. Скорость изменения мгновенного значения определяется АКФ процесса:

                                              (18)

                                                                           (19)

Подставляя в (19)

                                       (20)

 

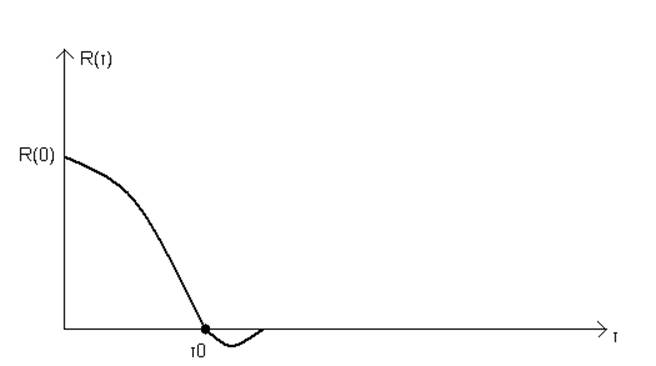
Время КБШ определяется из (20):

                                                                                                             (21)

БШ.

Описан в конце лекции 13. Эта модель ФП с постоянной спектральной плотностью  на бесконечном интервале частот .

Для БШ:

                                                               (22)

Из (22) следует, что БШ является дельта-коррелированным, что означает бесконечно высокую скорость изменения его мгновенных значений.

СП y(t) однозначно определяется некоторой совокупностью своих значений и следовательно принятая реализация при отсутствии сигнала y(t)=n(t) может быть заменена многомерной величиной.

 

Такая замена производится на основании теоремы Котельникова, по которой любая функция с ограниченным спектром полностью определяется отсчетами своих значений, взятых через интервал                        (23)

В соответствии с теоремой Котельникова:

                                                                                      (24)

 - элемент выборки СП в дискретные моменты времени.

 

 

Процесс (24) подчинен нормальному закону:

 – не коррелированны, так как  (время корреляции) (формула (21)), а поэтому коэффициенты разложения являются независимыми статистическими величинами.

Статистика принятого сигнала, обусловленного только помехой, описывается многомерной плотностью вероятности. При использовании теоремы Котельникова случайные коэффициенты разложения y₁, y₂, …, y_m независимы, а потому:

                                                                                            (25)

 - одномерная плотность (формула (17)).

Произведя замену:

 

Окончательно получим:

                                                                         (26)

б) Смесь сигнал + помеха.

В принятом полезном сигнале x(t, α, β) (α – параметр, подлежащий измерению в процессе обработки), (β – параметр не несущий информации).

Рассмотрим 3 модели сигналов:

1) x(t, α) – сигнал с полностью известными параметрами.

2) x(t, α, φ) – сигнал со случайной начальной фазой.

3) x(t, α, φ, β) – сигнал со случайной амплитудой и начальной фазой.

Для первой модели принятая реализация:

y(t) = n(t) + x(t, α)

по теореме Котельникова представляется в виде множества:

 

 - неслучайные величины, выполняющие роль математического ожидания для .

Многомерная плотность вероятности принятого сигнала первой модели:

                                   (27)

Для второй и третьей моделей  зависит от случайных параметров, поэтому сначала определяется  в соответствии с (27), а затем производит ее усреднение по плотности вероятности случайных параметров β.

                                                                               (28)

Для второй модели: .

Для третьей модели: .

Статистика принятого сигнала полностью описывается (27) и (28), которые используются для вычисления отношения правдоподобия и нахождения по нему алгоритма оптимального приема каждой модели сигнала.