Задача № 2.
Расчёт четырёхполюсной цепи .
Для заданной схемы четырёхполюсника требуется :
1. Представить сложный четырёхполюсник в виде двух простых и определить способ их соединения .
2. Определить коэфициенты матрицы А, элементы четырёхполюсника и коэффициенты других матриц, соответствующих соединению четырёхполюсника.
3. Использовать правила сложения и умножения матриц,определяя коэфициенты матрицы А составного четырёхполюсника.
4. Определить собственные и рабочие параметры составного четырёхполюсника (Zc1,Zc2,g,a,b,Zвх1,Zвх2,Араб.,Авн.).
5. Рассчитать и построить зависимости модуля и аргумента входного сопротивления четырёхполюсника от сопротивления нагрузки Zвх1(Rн),fвх1(Rн).
6. Записать уравнения передачи четырёхполюсника в матричной ипарраллельных формах.
Исходные данные:
![]()
![]()
![]()
![]()
![]()
Ом
![]()
Ф
![]()
![]()
Гн
![]()
Гц
![]()
Решение :
1. Представим сложный ЧП в виде двух простых и определим способ их соединения :
- Последовательно-параллельное соединение двух четырехполюсников
![]()
![]()
1/с
2. Определим коэффициенты матрицы А элементарных ЧП, а также коэффициентов других матриц, соответствующих соединению ЧП.
![]()
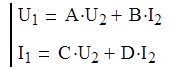
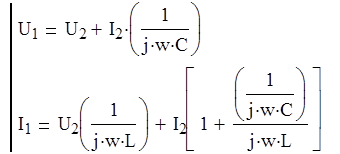
=>
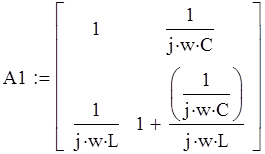
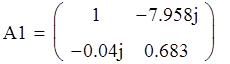
Определим по формулам перехода коэффициенты матрицы Y :
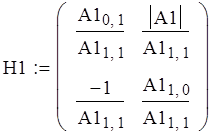
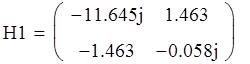
б).
Определим коэффициенты матрицы А, используя непосредственное применение законов Ома и Кирхгоффа ,сответствующих соединению ЧП :
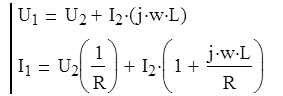
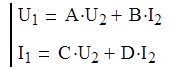
=>
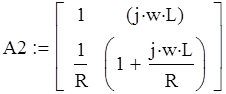
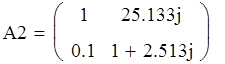
Так как при послеловательно-параллельном соединениии выходные зажимы перекрещены, следовательно запишем матрицу А2' :
![]()
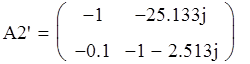
![]()
Определим по формулам перехода коэффициенты матрицы Y :
![]()
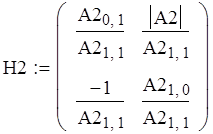
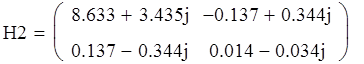
в). Определим коэффициенты матрицы Y сложного ЧП :
![]()
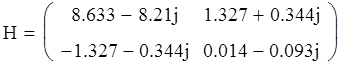
3. Определим коэффициенты матрицы А сложного ЧП ( матрицу А обозначим Ач):
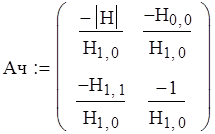
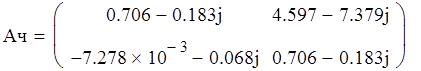
![]()
4. Определим собственные и рабочие параметры составного ЧП :
Так как сложный ЧП является симметричным, что видно из схемы в пункте 1(т.е. данный сложный ЧП можно разделить на две части осью симетрии) характериастическое сопротивление его равно :
![]()
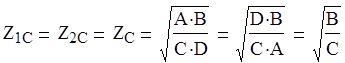
a).
Коэффициенты А, В, С, D, найдем из матрицы А
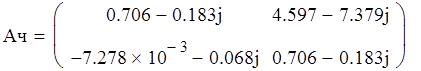
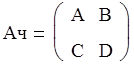
![]()
![]()
![]()
![]()
![]()
![]()
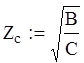
![]()
Ом
![]()
Ом
![]()
б). Определим собственную характеристическую постоянную передачи ЧП:
![]()
![]()
Нп
![]()
Нп
![]()
в). Определим a - характеристический коэффициент затухания ЧП и
b - характеристический коэффициент фазы.
![]()
![]()
![]()
Нп
![]()
Нп где Re - действительная часть комплексного числа (постоянной передачи)
Im - мнимая часть комплексного числа (постоянной передачи)
г). Определим входные сопротивления ЧП : Zвх1 и Zвх2
Так как составной ЧП - симметричный, то
![]()
![]()
![]()
Ом
![]()
Ом
![]()
д). Определим рабочее и вносимое ослабление :
![]()
Ом
Определим k1 и k2 - коэффициенты отражения (несогласованности) на входе и выходе.
Так как сложный ЧП является симметричным, то характеристическое сопротивление его равно :
![]()
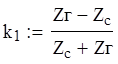
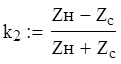
![]()
![]()
![]()
![]()
![]()
![]()
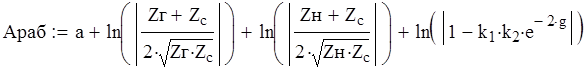
![]()
Нп
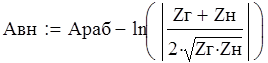
![]()
Нп
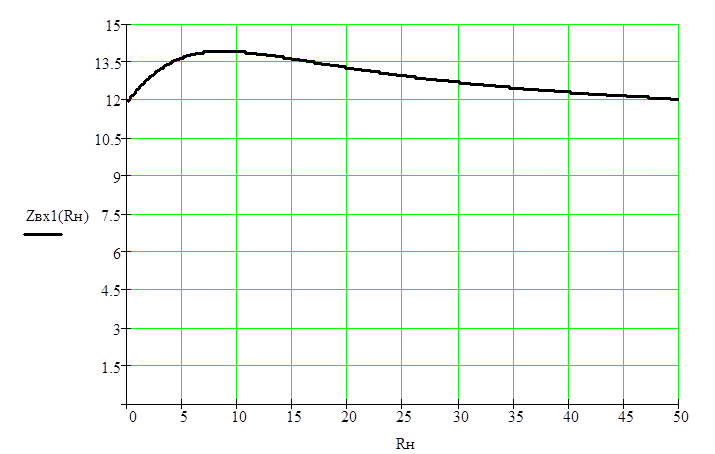
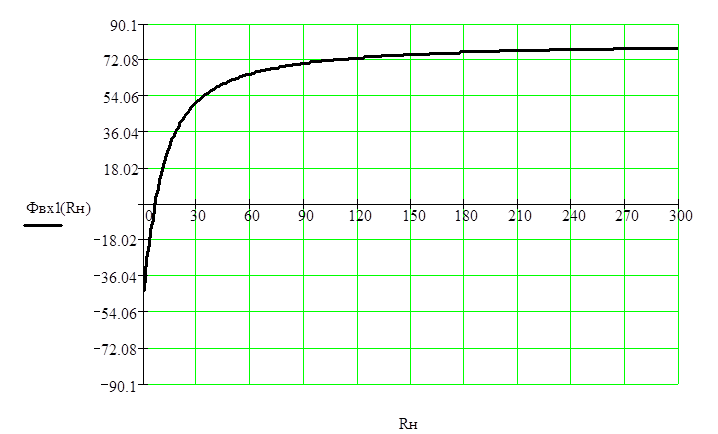
5. Рассчитаем и построим зависимости модуля и аргумента входного сопротивления составного ЧП от сопротивления нагрузки :
![]()
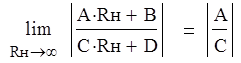
![]()
![]()
![]()
![]()
![]()
![]()
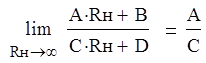
![]()
6. Запишем уравнения передачи ЧП в матричной и параметрической формах :
a). Матричная форма :
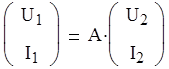
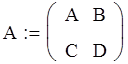
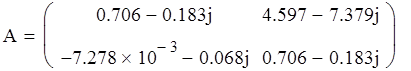
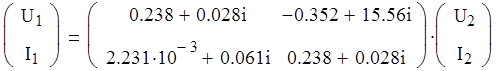
б). Параметрическая форма :
Для симметричного четырёхполюсника имеет вид :
![]()
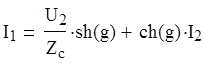
где g-собственная характеристическая постоянная передачи ЧП
в данных уравнениях через g мы выразили характеристичесие постоянные ослабления и фазы т.к. четырех полюсник можно полностью охарактеризовать через характеристические сопротивления и постоянную передачи.
Так как
![]()
Нп
![]()
![]()
![]()
Ом
![]()
![]()
Следовательно уравнения передачи ЧП в параметрической форме следующие :
![]()

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.