Синтез дискретных устройств. Рассмотрение ряда базовых вопросов построения логических устройств с жесткой логикой на базе современных интегральных схем, страница 5

Задание 2         

По заданию необходимо построить асинхронный автомат по известным таблицам переходов и выходов.

Асинхронный автомат это устройство, которое работает без использования синхронищзации.

Составим  алгоритм работы асинхронного автомата и запишем его в табличной форме [таблица 9]. Данная таблица составляется следующим образом:

По таблице переходов [таблица 7] составим линомы, которые представляют собой одни и те же состояния при фиксированном состоянии входа  ‘а’ автомата.

Затем произвольным образом закодируем линомы двоичным кодом. Так как в нашем случае четыре линома, то для их кодировки нам понадобится две переменные y1, y2.

По таблице выходов [таблица 8]  проставим состояния выхода автомата.

Эти действия необходимо проделать для двух состояний входа ‘a’ асинхронного автомата, а=0 и а=1.

Составим таблицу воздействий [таблица 10]. Она представляет собой упрощенный вариант таблицы 9.

Так как для работы автомата нам необходимо четыре входных воздействия, y1, y2, y3, y4, то составим обобщенную таблицу воздействий [таблица 11], в которую запишем состояние выхода автомата при всех комбинациях входных воздействий, y1, y2, y3, y4, a. Причем в этой таблице запишем нулевое состояние выхода автомата при тех комбинациях входных воздействий которые не используются для работы автомата.

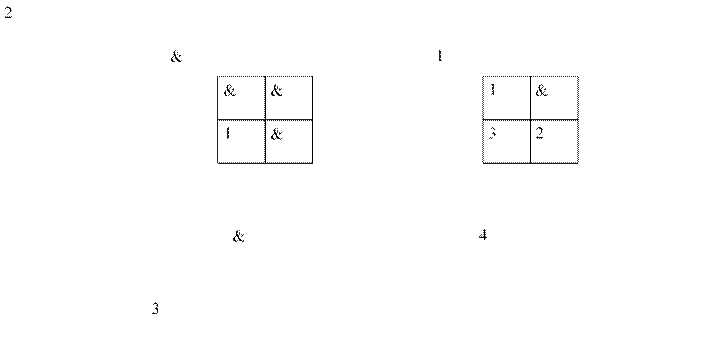
Перезапишем таблицу 11 с учетом использования в качестве элементов памяти jk - триггеров [таблица 13]. Алгоритм работы jk - триггера приведен в таблице 12. Минимизация логических функций необходимых для работы jk - триггеров представлена на рисунке 12.