Делитель частоты - это устройство, которое при подаче на его вход периодической импульсной последовательности формирует на выходе такую же импульсную последовательность, но имеющую частоту повторения импульсов в заданное число раз меньше чем во входной последовательности. Для работы мультиплексора необходимо на адресные входы подать импульсную последовательность определенной частоты. Частота импульсной последовательности зависит от количества информационных входов (в нашем случае 5 входов), т.е. информация на адресных входах мультиплексора должна изменяться в пять раз быстрее, чем на информационных. Для этого синтезируем делитель частоты с коэффициентом пять. В качестве делителя частоты используем микросхемы К555ТВ9, которые содержат по два JK - триггера [3]. Делитель частоты строим по методу построения двоичного счётчика с коэффициентом счёта ксч=5.
Определим число триггеров путём перевода ксч, заданного в десятичной форме в двоичную систему счисления:
2к-1
52к
Отсюда, к = 3, т.е. необходимо три триггера;
Составим таблицу 1 – таблицу состояний JK – триггера, а в таблицу 2 занесем предыдущее и последующее состояние счётчика, а также состояния входов триггеров:
Таблица 1 |
||
Переход |
Входы |
|
|
J |
K |
|
|
0 ® 0 |
0 |
~ |
|
0 ® 1 |
1 |
~ |
|
1 ® 0 |
~ |
1 |
|
1 ® 1 |
~ |
0 |
Таблица 2 |
||||||||||||
|
№ |
Предыдущее состояние |
Последующее состояние |
Сигналы на информационных входах триггеров |
|||||||||
|
Q3n |
Q2n |
Q1n |
Q3n+1 |
Q2n+1 |
Q1n+1 |
J3 |
K3 |
J2 |
K2 |
J1 |
K1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
~ |
0 |
~ |
1 |
~ |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
~ |
1 |
~ |
~ |
1 |
|
2 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
~ |
~ |
0 |
1 |
~ |
|
3 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
~ |
1 |
~ |
1 |
|
4 |
1 |
0 |
0 |
0 |
0 |
0 |
~ |
1 |
0 |
~ |
0 |
~ |
Используя методику минимизации не полностью определенных логических функций с помощью карт Карно, найдем:
 |
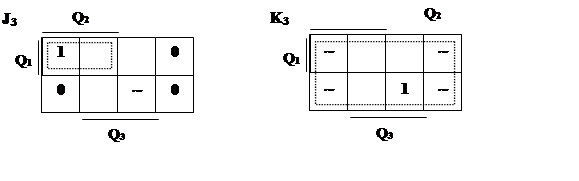K3=1
 |
 |
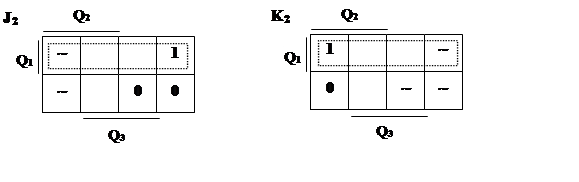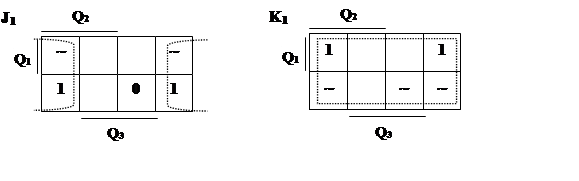K1=1
Переведем функции в базис И-НЕ:
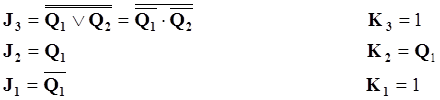
На рисунке 1.3.1 представлена структурная схема делителя частоты с kсч=5.
 |
|||
|
|||
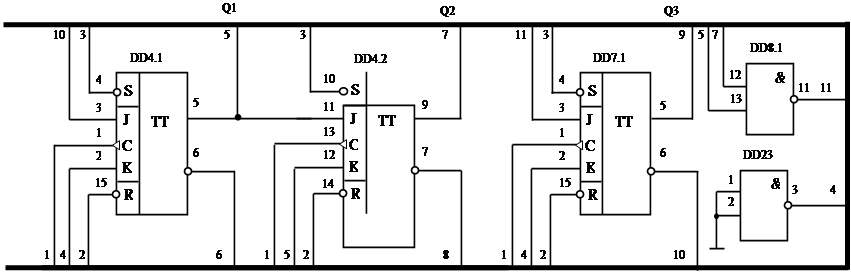На рисунке 1.3.2
представлена временная диаграмма работы делителя частоты.
|
|||||||||
 |
|||||||||
|
|||||||||
 |
|||||||||
 |
|||||||||
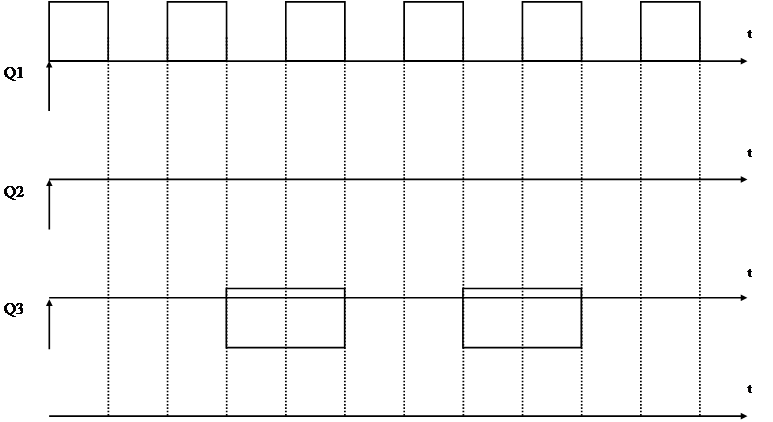По заданию необходимо провести минимум один раз минимизацию методом Квайна. Минимизируем функцию J2:
Запишем СДНФ функции J2, полученную из функции J2 путём задания единиц на некоторых неопределённых наборах аргументов и произведём попарное склеивание:
Составим импликантную таблицу из всех членов функции J2 (таблица 2.1):
Таблица 2.1
|
|
|
|
|
|
|
|
1 |
|
-- |
|
|
|
|
1 |
|
-- |
|
|
-- |
|
1 |
|
|
|
|
-- |
|
1 |
Продолжим минимизацию функций (таблица 2.2):
Таблица 2.2
|
|
|
|
|
|
|
|
1 |
-- |
-- |
|
|
|
-- |
1 |
|
-- |
|
|
-- |
|
1 |
-- |
|
|
|
-- |
-- |
1 |
Результат минимизации: J2=Q1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
