Сравнивая соседние группы, получим разложение 1-го ранга:
1группа:-001, 0-01, 00-1
2 группа:1-01, -101, 10-1, -011, 01-1, 0-11
Теперь находим члены разложения 2-го ранга:
1 группа:--01, -0-1, 0--1
Составим импликантную таблицу
|
0001 |
1001 |
0101 |
0011 |
1101 |
1011 |
0111 |
|
|
--10 |
|
|
|
|
|||
|
-0-1 |
|
|
|
|
|||
|
0--1 |
|
|
|
|
Q3Q1Q4Q1 =(Q2 Q1) (Q3 Q1) (Q4
Q1) По полученным выражениям построена схема счетчика, изображенная на рисунке 1.3.1.
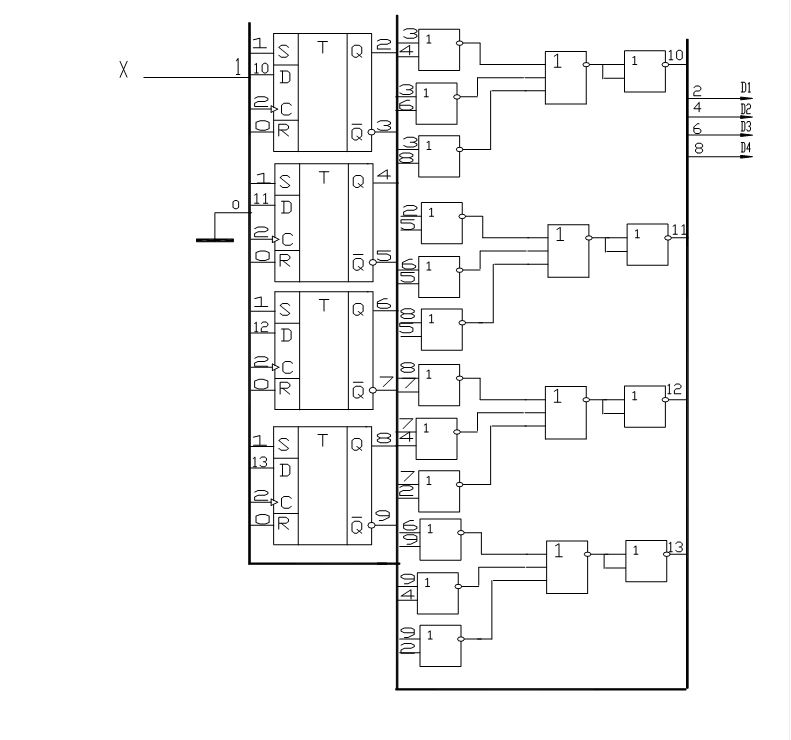
Рисунке 1.3.1 Принципиальная схема счетчика
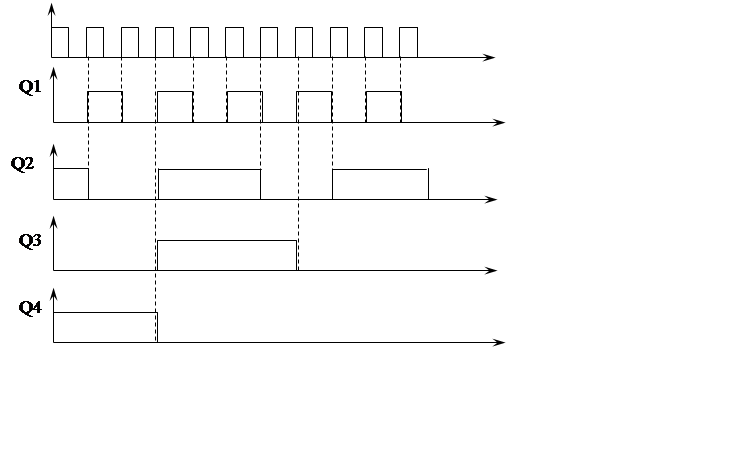
t
t
t
t
t
Рисунок 1.3.2 Временная диаграмма работы счётчикаНеобходимо построить преобразователь из кода 8421 в код с избытком 3 в базисе ИЛИ-НЕ.
Преобразователем кодов называется устройство для преобразования одного вида двоичного кода в другой. Преобразователи используются для повышения помехоустойчивости процесса передачи информации. Двоичные сигналы с помощью преобразователя кодируют , то есть придают некоторый признак, по которому на приемной стороне можно сказать, произошла или не произошла ошибка при передачи сообщения [1, c.23] .
Код с избытком 3 представляет интерес тем, что в нем кодовая комбинация, соответствующая любой из десятичных цифр, представляет собой инверсию комбинации , необходимую ей для дополнения до девяти .
Функционирование преобразователя кодов задано табл.1.4.1.
Таблица 1.4.1 Таблица истинности преобразователя кодов
|
Десятичные шифры |
Вход (8421) |
Выход(с избытком 3) |
|||||||
|
D4 |
D3 |
D2 |
D1 |
Y5 |
Y4 |
Y3 |
Y2 |
Y1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
7 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
8 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
9 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
10 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
12 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
13 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
14 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
Запишем СДНФ для выходов преобразователя Y1, Y2, Y3, Y4, Y5.
Y1= D4D3D2D1D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1
D4D3D2D1 D4D3D2D1
Y2= D4D3D2D1D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1
D4D3D2D1
Y3= D4D3D2D1D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1
D4D3D2D1 D4D3D2D1
Y4= D4D3D2D1D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1 D4D3D2D1
D4D3D2D1 D4D3D2D1
Y5= D4D3D2D1D4D3D2D1 =(D4 D3 D2 D1)
( D4 D3 D2 D1)
Минимизируем функции выходов преобразователя кодов Y1, Y2, Y3, Y4 методом Квайна-Мак-Класски (таблицы 1.4.2-1.4.4).
Выход преобразователя кодов Y1:
Запишем члены разложения СДНФ по группам в двоичном коде:
0 группа:0000
1 группа:0010, 0100, 1000
2 группа:0110,1010, 1100
3 группа:1110
Сравнивая соседние группы, получим разложение 1-го ранга:
0 группа:00-0, 0-00, -000
1 группа:0-10, -010, 01-0, -100, 10-0, 1-00
2 группа:-110, 1-10, 11-0
Находим члены разложения 2-го ранга:
0 группа:0--0, -0-0, --00
1 группа:--10, -1-0, 01-0, 1—0
Находим члены разложения 3-го ранга:
0 группа:---0
 |
Y1=D1
Выход преобразователя кодов Y2:
Запишем члены разложения СДНФ по группам в двоичном коде:
0 группа:0000
1 группа:0100, 1000
2 группа:0011, 1100
3 группа:0111, 1011
Сравнивая соседние группы, получим разложение 1-го ранга:
0 группа:0-00, -000
1 группа:-100, 1-00
2 группа:0-11, -011
Находим члены разложения 2-го ранга:
0 группа:--00, -0-0, --00
2 группа:0-11, -011
Составим импликантную таблицу:
|
0000 |
0100 |
1000 |
0011 |
1100 |
0111 |
1011 |
|
|
--00 |
|
|
|
|
|||
|
0-11 |
|
|
|||||
|
-011 |
|
|
D4D2D1D3D2D1 =(D2
D1) (D4 D2 D1) (D3 D2
D1)Выход преобразователя кодов Y3:
Запишем члены разложения СДНФ по группам в двоичном коде:
1 группа:0001, 0010, 0100
2 группа:0011, 1001, 1010,1100
3 группа:1011
Сравнивая соседние группы, получим разложение 1-го ранга:
1 группа:00-1, -001, 001-, -010, -100
2 группа:-011, 10-1, 101Находим члены разложения 2-го ранга:
1 группа:-0-1, -01-, -100
Составим импликантную таблицу:
|
0001 |
0010 |
0011 |
0100 |
1001 |
1010 |
1011 |
1100 |
|
|
-0-1 |
|
|
|
|
||||
|
-01- |
|
|
|
|
||||
|
-100 |
|
|
D3D2D3D2D1 =(D3
D1) (D3 D2 ) (D3 D2 D1)Выход преобразователя кодов Y4:
Запишем члены разложения СДНФ по группам в двоичном коде:
1 группа:1000
2 группа:0101, 0110, 1001, 1010, 1100
3 группа:0111, 1011
Сравнивая соседние группы, получим разложение 1-го ранга:
1 группа:100-, 10-0, 1-00
2 группа:01-1, 011-, 10-1, 101Находим члены разложения 2-го ранга:
1 группа:10--, 1-00
2 группа:01-1, 011Составим импликантную таблицу:
|
1000 |
0101 |
0110 |
1001 |
1010 |
1100 |
0111 |
1011 |
|
|
10-- |
|
|
|
|
||||
|
01-1 |
|
|
||||||
|
011- |
|
|
||||||
|
1-00 |
|
D4D3D1D4D3D2D4D2D1=(D4
D3) (D4 D3 D1) (D4 D3 D2)
(D4D2D1)По полученным выражениям построена схема преобразователя кодов, изображенная на рисунке 1.4.1.
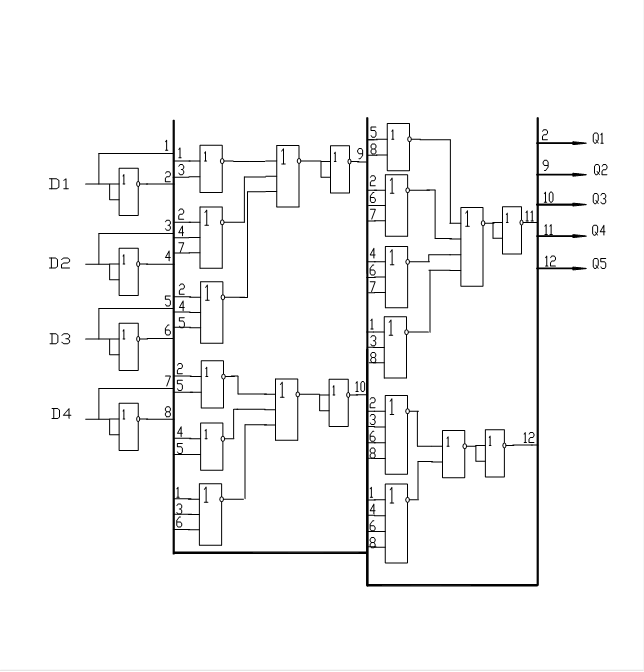
Рисунок 1.4.1 Cхема преобразователя кодов
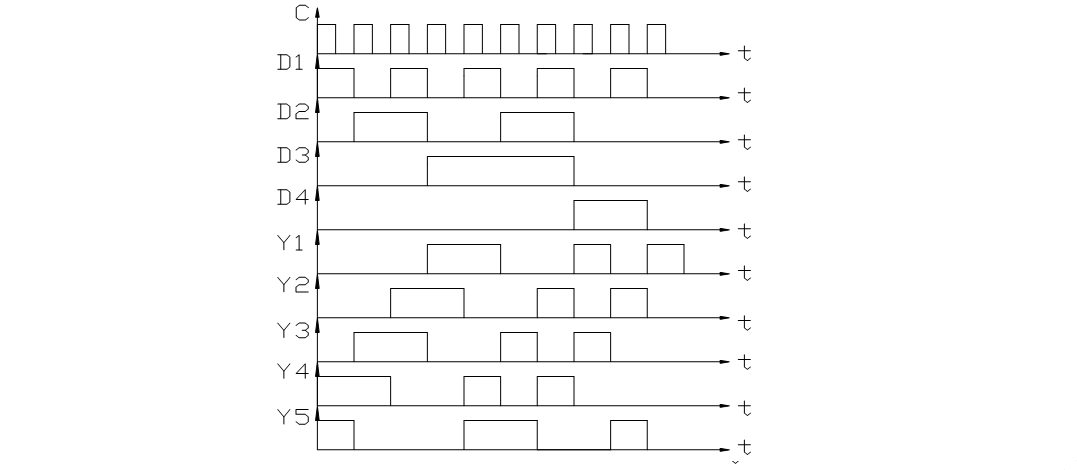
Рисунок 1.4.2 Временная диаграмма работы преобразователя кодов
Делитель частоты - устройство, которое при подаче на его вход периодической импульсной последовательности формирует на выходе такую же последовательность но имеющую частоту повторения импульсов, в определенное число раз меньшую, чем частота повторения импульсов входной последовательности.
По заданию необходимо чтобы на выходе частота импульсов была в 30 раз меньше, чем на входе. Для синтеза делителя частоты будем использовать JK-триггеры с динамическим управлением.
Деление частоты произойдет, когда на триггерах А, В, С, Е на выходе будет логическая «1», а на триггере D – логический «0». Таким образом на выходе будет
 |
Y=A
BCDE
Преобразуем полученное выражение к базису ИЛИ-НЕ:
 |
|||||||
 |
 |
|
|||||
Y=A B C D E
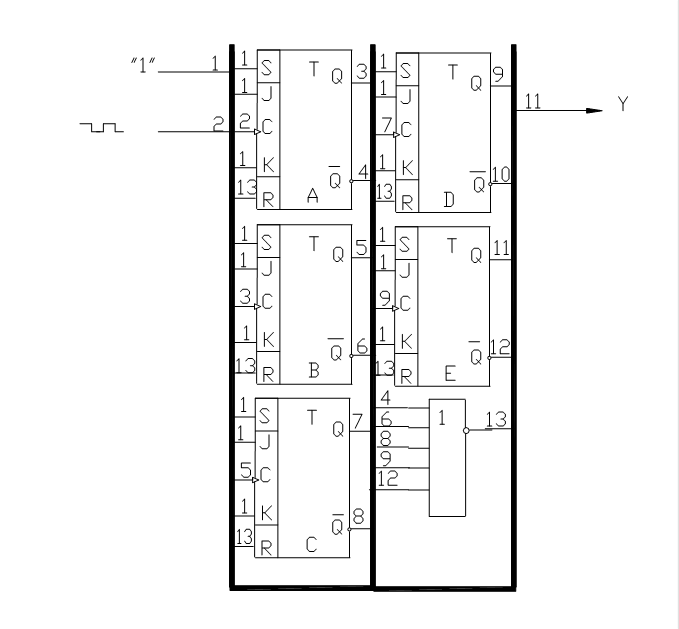
Рисунок 1.5.1 Принципиальная схема делителя частоты
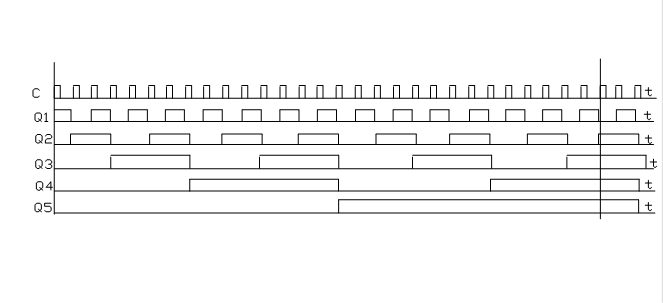
Рисунок 1.5.2 Временная диаграмма работы делителя частоты
Сумматор - дискретное устройство, выполняющее операцию сложения по модулю два . Сумматор служит для выполнения операций сложения и вычитания чисел представленных в двоичной системе счисления . Сумматоры относятся к классу комбинационных схем.
Многоразрядный сумматор состоит из отдельных одноразрядных сумматоров. Каждый из одноразрядных сумматоров формирует на своих выходах соответствующий разряд суммы и перенос передаваемый на вход следующего более старшего разряда.
Так как по схеме сумматор будет складывать выходные сигналы преобразователя кода и делителя частоты, то наш сумматор будет состоять из пяти одноразрядных сумматоров.
В качестве сумматора будем использовать сумматор ИМ5, выполненный на микросхеме К555ИМ5. Микросхема К555ИМ5 представляет собой два одинаковых одноразрядных двоичных полных сумматора. Он выполняет операцию сложения двух одноразрядных чисел в двоичном
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
