Другие предметы \ Теория дискретных устройств

Разработка дискретного устройства. Схема электрическая принципиальная дискретного устройства. Схема абстрактного автомата, электрическая принципиальная, страница 2


Так как мы знаем выходную частоту генератора f=100 кГц, то исходя из формулы найдём номиналы резистора R и конденсатора C:

Взяв конденсатор номиналом 6,8 нФ,  мы получим номинал резистора равный 490 Ом. Для точной установки номинала резистора будем использовать два резистора: подстроечный резистор серии СП3 и резистор серии МЛТ.

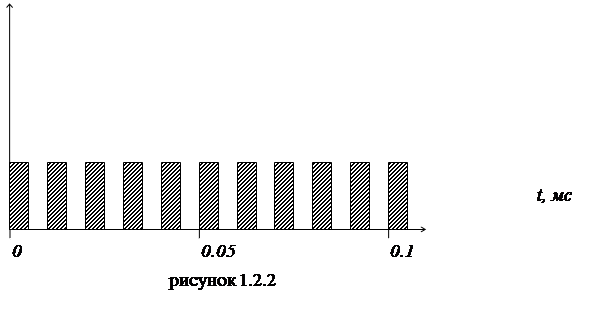
Для наглядной демонстрации работы генератора на рисунке 1.2.2  представлена временная диаграмма.

 



1.3 Разработка счётчика.

 


Счётчик специальное устройство считающее поступившие на вход активные сигналы.

В данном варианте курсового проекта нам необходимо построить вычитающий двоичный счётчик на D-триггерах с коэффициентом счёта 15. Под коэффициентом счёта равным 15 будем понимать, что максимальное состояние счётчика 15. Счётчик имеет 16 состояний начиная с состояния 0. Вид выходного кода 2421. Для хранения 16 разных состояний в коде 2421 понадобиться пять D-триггеров.  Код 2421 для 16 состояний представлен в таблице 1.3.1

Таблица 1.3.1

№

Код

№

Код

0

00000

8

01110

1

00001

9

01111

2

00010

10

10000

3

00011

11

10001

4

00100

12

10010

5

01011

13

10011

6

01100

14

10100

7

01101

15

11011

На основе таблицы 1.3.1 сформируем таблицу переходов счётчика на пяти триггерах (таблица 1.3.2).

Таблица переходов.                 Таблица 1.3.2

№

состояния

Тек. сост.

Посл. сост.

Выход

Q1 Q2 Q3 Q4 Q5

Q1 Q2 Q3 Q4 Q5

D1 D2 D3 D4 D5

15

1 1 0 1 1

1 0 1 0 0

1 0 1 0 0

14

1 0 1 0 0

1 0 0 1 1

1 0 0 1 1

13

1 0 0 1 1

1 0 0 1 0

1 0 0 1 0

12

1 0 0 1 0

1 0 0 0 1

1 0 0 0 1

11

1 0 0 0 1

1 0 0 0 0

1 0 0 0 0

10

1 0 0 0 0

0 1 1 1 1

0 1 1 1 1

9

0 1 1 1 1

0 1 1 1 0

0 1 1 1 0

8

0 1 1 1 0

0 1 1 0 1

0 1 1 0 1

7

0 1 1 0 1

0 1 1 0 0

0 1 1 0 0

6

0 1 1 0 0

0 1 0 1 1

0 1 0 1 1

5

0 1 0 1 1

0 0 1 0 0

0 0 1 0 0

4

0 0 1 0 0

0 0 0 1 1

0 0 0 1 1

3

0 0 0 1 1

0 0 0 1 0

0 0 0 1 0

2

0 0 0 1 0

0 0 0 0 1

0 0 0 0 1

1

0 0 0 0 1

0 0 0 0 0

0 0 0 0 0

0

0 0 0 0 0

1 1 0 1 1

1 1 0 1 1

По таблице переходов построим функции алгебры логики и минимизируем их с помощью метода Квайна.

 


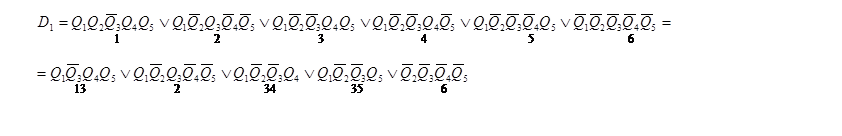
1

2

3

4

5

6

13

V

V

2

V

34

V

V

35

V

V

6

V
Скачать файл