Дискретные устройства. Разработка дискретного устройства. Генератор импульсов. Временная диаграмма работы генератора, страница 3

           1.5 Сумматор по модулю 2

Принцип работы сумматора по модулю 2 можно записать в виде таблицы:

Таблица 1.3. Зависимость входы-выход для сумматора по модулю 2

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	0

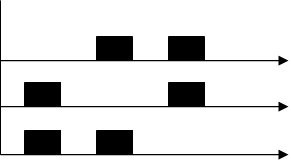
Диаграмма работы такого устройства выглядит следующим образом:

 

X₁

X₂

Y

Рис 1.8. Временная диаграмма работы сумматора по модулю 2

 

X₁

 

X₂

 

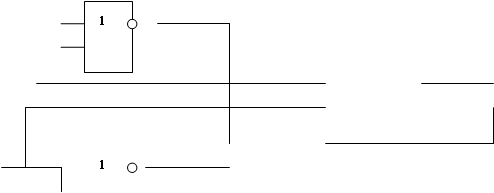
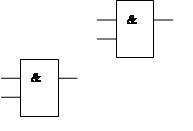
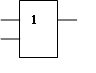
Рис 1.9. Схема сумматора по модулю 2

 

2 Синтез абстрактного автомата

                2.1 Задание исходных данных

Абстрактный автомат – это устройство изменяющее свои состояния под воздействием входных сигналов. Синхронный автомат характерен тем, что переключения его триггеров заранее известны. Синхронный автомат имеет ряд преимуществ перед асинхронными, как то простота исполнения, отсутствие критических состязаний, и др.

Для синтеза данного автомата использовался графический метод (граф автомата приведен в приложении) [построение графа см. л3.43]. Последовательность применения графического метода приведена ниже. Построим в соответствии с заданием таблицу переходов и таблицу выходов.

Таблица 2.1. Таблица переходов

a S	X	X
S0	S1	S0
S1	S2	S1
S2	S0	S3
S3	S3	S4
S4	S4	S2

Таблица 2.2. Таблица выходов

a S	a1	a2
S0	1	1
S1	1	1
S2	0	0
S3	0	0
S4	0	0

Закодируем состояния автомата

S0=000 S1=001 S2=010 S3=011 S4=100

Отсюда видно, что для синтеза автомата понадобиться всего три  

D-триггера. По построенному графу составим функции возбуждения и выхода автомата.

 

D_A=ABCX v ABCX v ABCX v ABCX

D_B=ABCX v ABCX

 

D_C=ABCX v ABCX v ABCX v ABCX

Y=ABCX v ABCX v ABCX v ABCX

Для нахождения неопределенных состояний необходимо найти так же инверсии этих функций.

D_A=ABCX v ABCX v ABCX v ABCX V ABCX v ABCX

 

D_B= ABCX v ABCX v ABCX v ABCX v ABCX v ABCX v ABCX v

 v ABCX