Наиболее часто в измерительной технике осуществляется квантование и дискретизация сигналов и их параметров. Процесс квантования сводится к представлению бесконечного числа значений непрерывных величин к конечному значению.
Квантованным сигналом называется физический процесс, основная характеристика которого принимает только квантованные значения.
Измерительные сигналы, у которых независимая переменная отличается от 0 только в определенных точках пространства и в определенные моменты времени называется дискретной.
Применяя комбинацию дискретизации и квантования получают 3 вида сигналов:
1. Непрерывные во времени и квантованные по значению информационного параметра.
2. Дискретные по времени или частоте с непрерывным по значению информационным параметром.
3. Дискретные по времени с квантованием по значению информационного параметра
При описании КС используются элементарные сигналы, к которым относятся: сигналы постоянного тока или напряжения, синусоидальные сигналы, единичные и импульсные сигналы.
X=A A=const постоянные сигналы;
X=d (t – tи) единичный импульс (дельта функция;
X=0 при t<>tи
X®¥ при t = tи
Параметр tи — указывает положение импульса на оси времени.
Единичный импульс обладает следующими свойствами:
Это означает то, что единичный импульс обладает стробирующим действием. Если X (t) = const.
Гармонический
сигнал широко применяется для синтеза измерительных сигналов.
Отдельный класс детерминированных сигналов — класс гармонических сигналов.
Ряд Фурье:
 |
 |
 |
 |
Если сигнал периодический, то спектр будет дискртный с огибающей:
 |
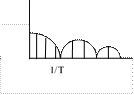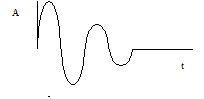При анализе
периодического сигнала рассматриваются следующие его параметры:
—
скважность
— среднее
значение постоянной
Средневыпрямленное значение:
Среднеквадратичное значение
В
математической модели используют сигналы, в которых основные спектральные
составляющие группируются в узкой полосе частот по сравнению с центральной
частотой.
где z — новая функция, которая связывается с x(t) соотношением.
Из него можно сделать выводы:
Функция x(t) — представляет собой проекцию вектора A(t)на ось абсцисс, относительно которой отсчитывается угол j(t). В тех точках, где z(t)=0, A(t)=x(t).
Также где z(t) = 0, там d A (t) dt = dx (t) dt
В точках где z (t) = 0 , там A(t) и x(t) имеют общие касательные.
Т. е. в точках, где z(t) = 0, x(t) принимает значения близкие к амплитуде, а функция A(t) — является огибающей быстроосциллирующей функции x(t).
Если
то:
В измерительной технике часто встречается сигнал измерительный, представленный в сумме двух гармонических колебаний с частотами w1 и w2, которые отстоят близко друг от друга.
Если D w = w2 - w1 << (w2 + w1)/2 , то сигнал считается узкополосным.
Отсюда огибающая A(t):
где к = A2 / A1
Используя эти выражения можно найти начальную фазу и мгновенную фазу начального колебания.
Данный сигнал называется «почти периодическим», т.к. образуется суммированием независимых периодических процессов.
Частотный спектр его является дискретным, хотя сигнал не периодический.
У непериодического сигнала спектр непрерывный. Описывается интегралом Фурье.
A и t — информационные параметры.
Постоянная затухания, t, A.
 |
Характеристики: Постоянная затухания, f, t, A.
Для этого используется разложение сигналов на сумму элементарных функций:
где Ai — коэффициент разложения;
ji — элементарная функция.
Для разложения сигнала на элементарные функции используют систему функций, которые удовлетворяют на интервале от tn до tk условию ортогональности:
при k<>n при k= 1…N; n=1…N.
jk (t) — является ортогональной, если:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
