Формирование матрицы соединений и матрицы главных контуров. Вектора источников токов, напряжений и диагональная матрица сопротивлений, страница 2

> restart:

> Uvh :=piecewise (t <= 0.003, 0, t >0.003 and t <= 0.015, 0.5, t > 0.015, 0 ) ;

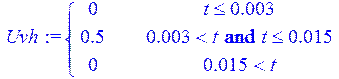
> plot(Uvh(t), t = -0.01 .. 0.02);

> with (linalg): with (inttrans):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the previous binding of the name hilbert has been removed and it now has an assigned value

Формируем  матрицу соединений и матрицу главных контуров:

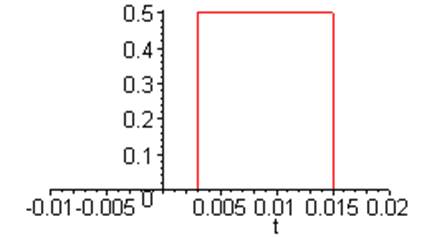
> A := matrix (3,5, [1,1,0,0,0,0,-1,1,1,0,0,0,0,-1,1] );

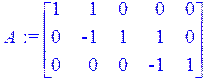
Задаём вектора источников токов, напряжений и диагональную матрицу сопротивлений:

> J := vector (5, [0,0,0,0,0] );

> E := vector (5, [E1,0,0,0,0] );

> Z := diag (Z1, Z2, Z3, Z4, Z5 );

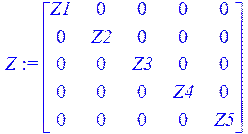
Выполняем транспонирование матрицы:

> At := transpose(A);

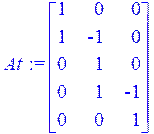
Сформируем уравнения контурных сопротивлений, контурных напряжений и  токов, а также  токов и напряжений в ветвях:

> Zk := multiply (A, Z, At);

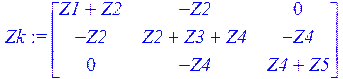
Распечатаем один из элементов матрицы контурных сопротивлений:

> Zk [1,1]; Zk [2,2];

> Ek := matadd ( multiply (A, E), - multiply (A, Z, J) ):

Таким образом, получили  систему контурных уравнений в матричном ном виде. Решая матричное уравнение   Zk * Ik = Ek  , находим вектор контурных токов:

> Ik := linsolve (  (Zk),  (Ek) );

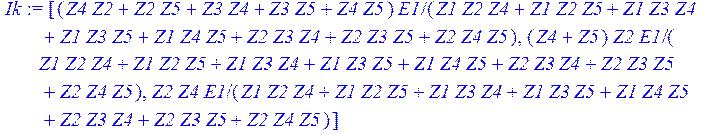
Далее находим вектора  токов и  напряжений в ветвях о общем виде:

> Ib := multiply (At, Ik);

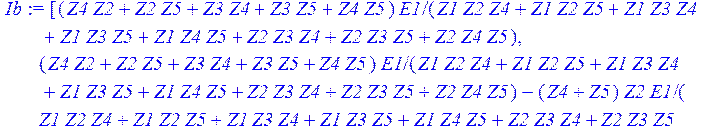
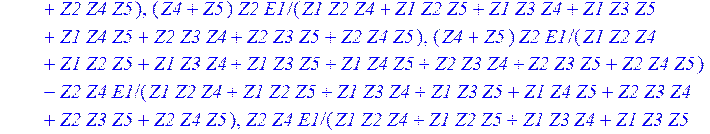
> Ic := matadd (Ib , J) ; 

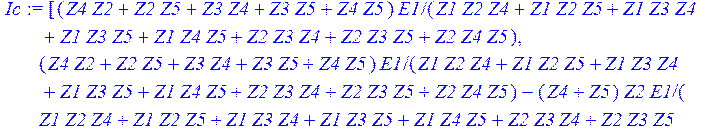
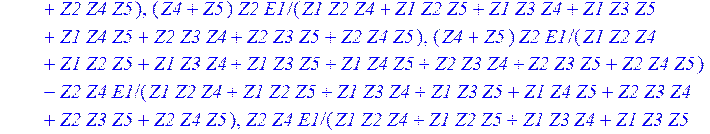
> Ub := matadd ( multiply (Z , Ic) ,  -E);

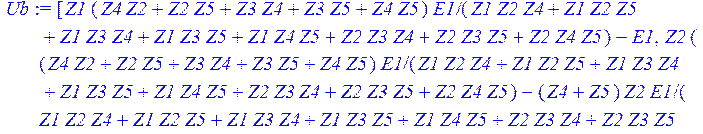
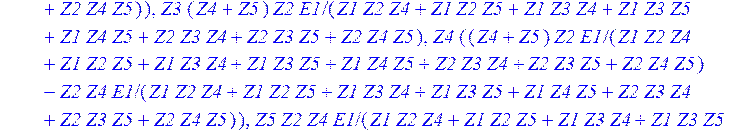
Теперь можно  найти передаточную функцию по напряжению, задать значения комплексных сопротивлений в операторной и частотной форме и построить АЧХ схемы.

Для нашей схемы передаточная функция по напряжению формируется как отношение напряжения в пятой ветви (напряжение на выходном резисторе) к напряжению источника сигнала.

> K := simplify (Ub[5]/E1);

Зададим  элементы схемы в операторном виде и получим выражение для передаточной функции в общем виде:

> Z1 := RL: Z2 := R1 + 1/(p*C1): Z3 := R3 + p*L1: Z4 := R2 + 1/ (p*C2):

> Z5 := RS + L2*p:

> K := simplify ( sort (expand(K) ) );

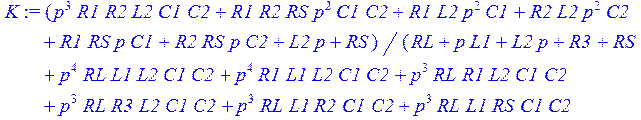
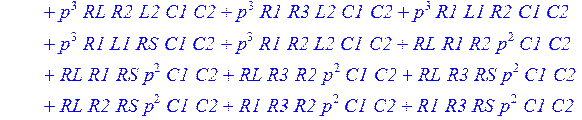
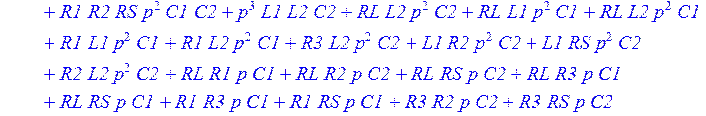
Зададим значения параметров элементов и источника сигнала (единичный импульс) в операторной форме:

> RL := 54: R1 := 4: R2 := 1: R3 := 0: RS := 80:

> L1 := 16*10^(-3): L2 := 6.0*10^(-3):

> C1 := 2.0*10^(-6): C2 := 5.3*10^(-6):

> E1 := laplace (Uvh, t, p);

Теперь выражение для передаточной функции примет следующий вид:

> K;

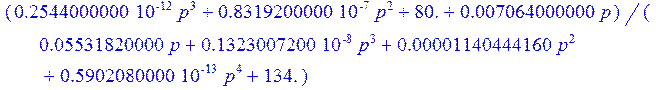
> Utt := simplify (invlaplace (K, p, t));

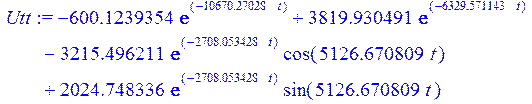
> plot (Utt, t = 0 .. 0.0025);

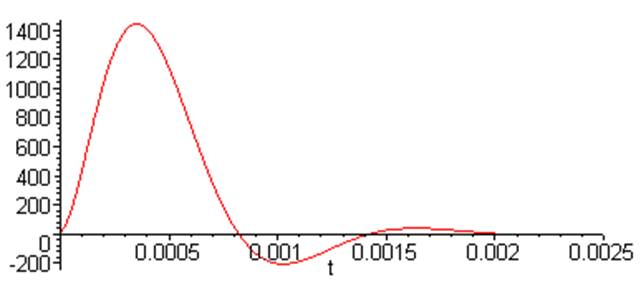
> Ub[5] := simplify (Ub [5]);

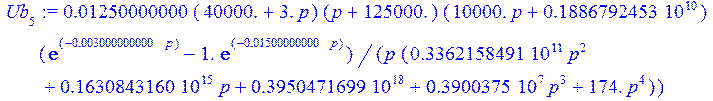
> Ubt [5] := simplify (invlaplace (Ub[5], p, t) );

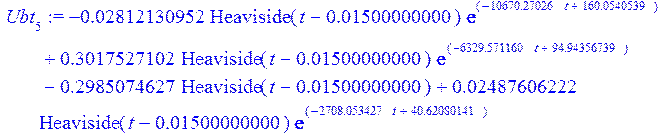
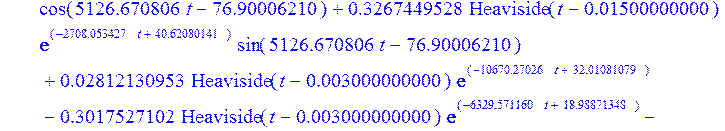
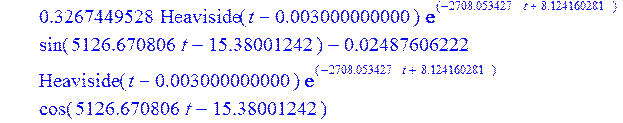
> plot (Ubt[5], t = -0.00001 .. 0.02);

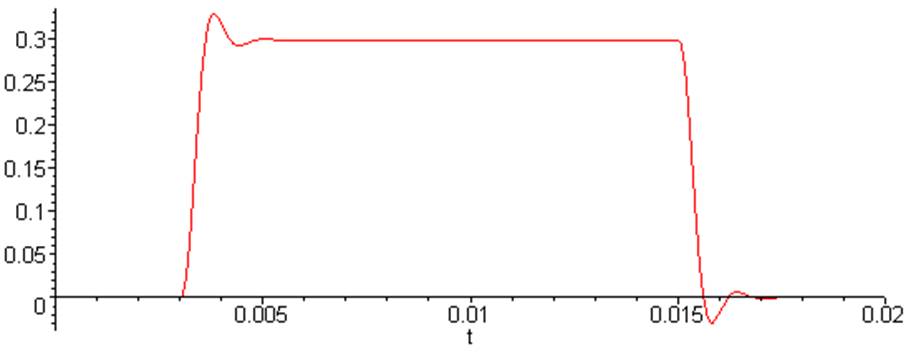
> Ubtt5 := diff (Ubt[5] , t );

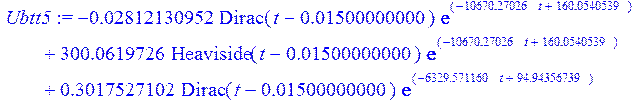
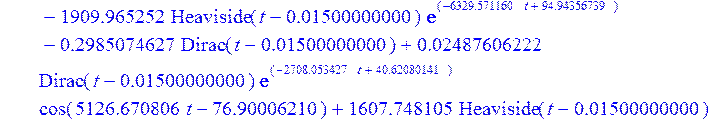
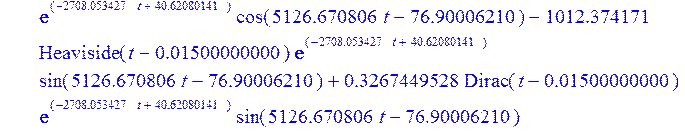
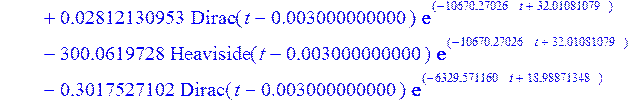
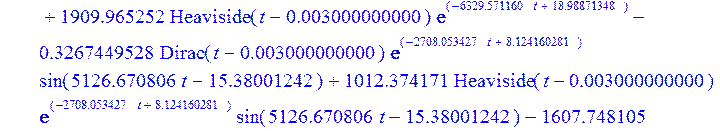
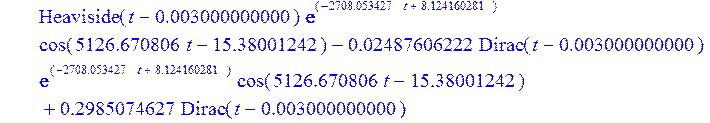
> plot (Ubtt5, t = -0.00001 .. 0.02);

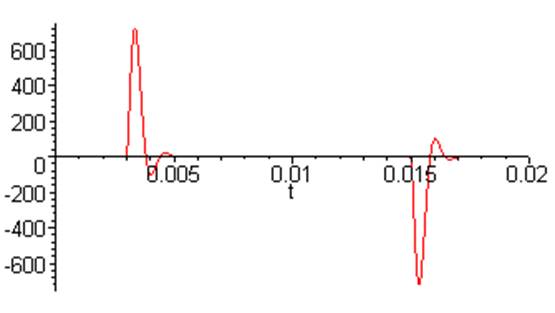
Упорядочим выражение и приведём различные его формы представления:

> K :=  sort( K );

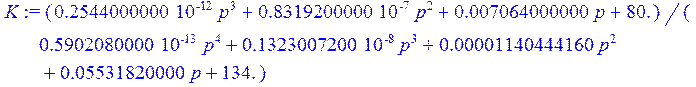
> factor( sort (K) );

Выделим числитель и знаменатель передаточной функции и запишем выражение для передаточной функции в виде отношения полиномов в переменную  RH:

> CH := sort (expand ( numer (K) ) );

> ZN :=  sort (expand (denom (K) ) );

> RH := CH / ZN;

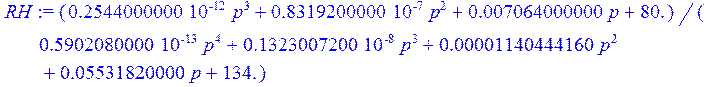
Выполним разложение выражения для передаточной функции на сумму дробно-рациональных функций:

> convert (RH , parfrac, p);

Найдём  корни характеристического полинома, значение которых позволяет оценить асимптотическую  устойчивость системы (по начальным данным):

> fsolve (ZN, p, complex);

Для примера распечатаем выражение для напряжения в 4-й ветви в операторной форме. Далее перейдём из операторной формы во временную и таким образом получим реакцию напряжения в 4-й ветви  на единичный импульс на входе системы (т.е. переходную функцию), запишем её в 4-й элемент вектора Ubt  и построим её график:

> Ub [4]  := simplify (Ub [4] );

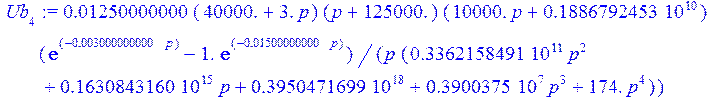
> Ubt [4] := simplify (invlaplace (Ub [4], p, t));

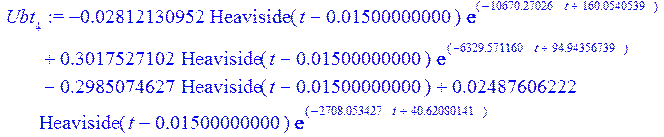
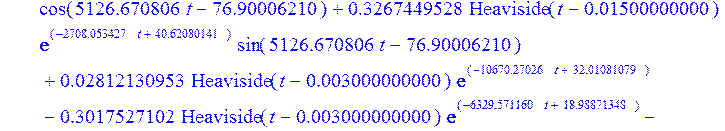
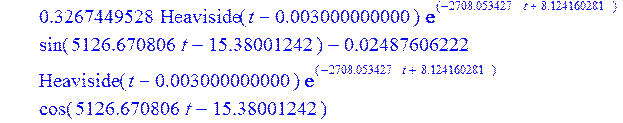
> plot (Ubt[4], t = 0.0035 .. 0.018);

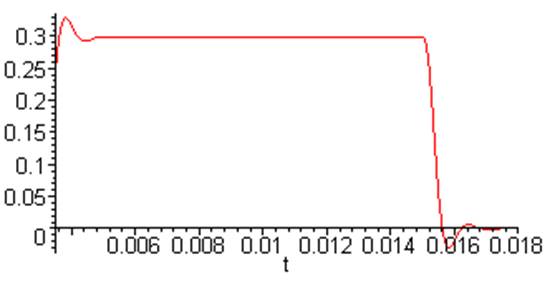
Выполним замену оператора p на jw после чего получим и построим график АЧХ системы:

> p := I*w: Kw := abs (evalf ( factor (K)) );

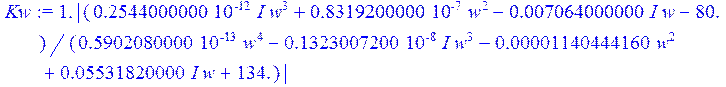
> plot (Kw , w = 1 .. 3000);

>

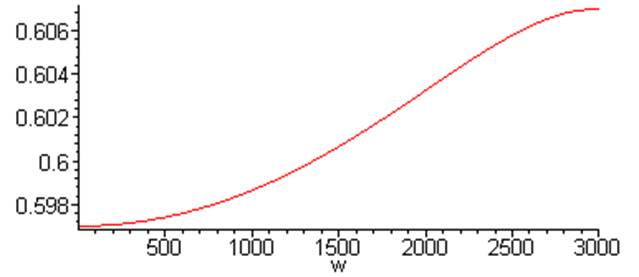
Вывод : Овладела навыками создания автоматизированных электронных документов синтеза систем уравнений, передаточных функций  и анализа динамических систем.