Получение статики модели по данным пассивного эксперимента. Формирование экспериментов с параллельными опытами

1.  Получение статики модели по  данным пассивного эксперимента

Исходные данные:

Пассивный эксперимент основан на регистрации контролируемых переменных в установившемся режиме эксплуатации объекта.

Изобразим объект с указанием всех переменных:

Х1,Х2 – входные переменные

Y – выходная переменная, зависящие от Х

Y_f – неконтролируемые входные факторы;

Y обусловлено действием всех входных переменных, т.е.

Статическая модель объекта устанавливает соответствие между входными и выходными переменными объекта в установившемся режиме.

№	Х1	Х2	Y
1	0,723	2,112	15,198
2	1,075	2,579	17,180
3	0,704	0,027	12,424
4	0,939	1,114	14,750
5	0,341	0,833	12,049
6	0,450	1,959	13,936
7	1,054	1,313	15,459
8	0,803	0,434	13,336
9	0,032	0,870	10,889
10	1,516	2,207	18,419
11	1,030	1,140	15,138
12	0,322	1,749	13,163
13	1,218	0,359	14,863
14	0,131	0,146	10,341
15	0,071	1,961	12,455
16	0,485	0,796	12,563
17	0,595	1,765	14,252
18	0,594	0,276	12,319
19	1,120	1,744	16,274
20	0,020	0,199	9,976
21	0,329	1,093	12,341
22	0,158	0,337	10,694
23	1,097	1,493	15,858
24	0,152	0,830	11,309
25	0,124	0,448	10,703

Формирование экспериментов с параллельными опытами

Результаты первого эксперимента:

Результаты второго эксперимента:

Пассивный эксперимент основан на регистрации контролируемых переменных в установившемся режиме работы  Регистрация происходит через длительные моменты времени, чтобы не было влияния измерений друг на друга.

Для обработки данных необходимо из каждого эксперимента учитывать только один опыт, поэтому из исходных данных  нужно убрать 1 измерение из первого эксперимента и 1 измерение из второго.

Оценка точности экспериментальных данных.

Расчёт математического ожидания и  выборочной дисперсии для каждого эксперимента

Для каждого эксперимента необходимо рассчитать σ²выб – выборочную дисперсию и mвыб – выборочное математическое ожидание, как оценку точности.

Выборочное мат. ожидание:

                                

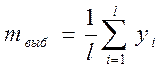
Выборочная дисперсия:

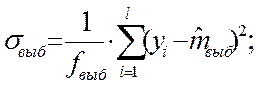
Для первого эксперимента:

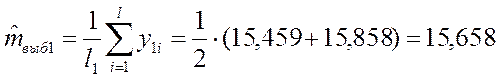
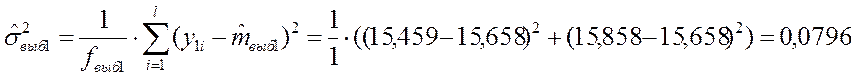
где  – число параллельных опытов в первом эксперименте;

         – число степеней свободы

Для второго эксперимента:

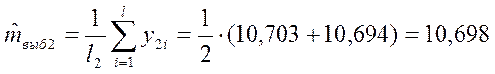
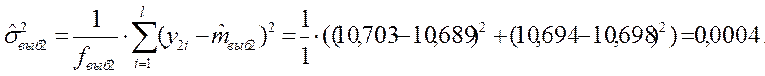
где  – число параллельных опытов во втором эксперименте;

             – число степеней свободы

Оценка однородности выборочных дисперсий

При проведении параллельных опытов необходимо определить являются ли результаты измерений в первом и во втором эксперименте статистически однородные (т.е. принадлежат ли все эти измерения одной генеральной совокупности случайных величин).

Первый эксперимент имеет генеральную дисперсию , а второй .

Выдвигается нулевая гипотеза : полагается, что обе выборки представляют собой совокупность независимых случайных величин и имеющие нормальный закон распределения

Нулевая гипотеза:

.

Выборочные дисперсии – это случайные оценки этой генеральной дисперсии, поэтому выдвигается альтернативная гипотеза .

Задаемся уровнем ошибки первого рода .

Для проверки такой нулевой гипотезы воспользуемся критерием Фишера   статистикой, которая зависит от  и двух  показателей степеней свободы  и . Причём всегда .

Кривая распределения Фишера.

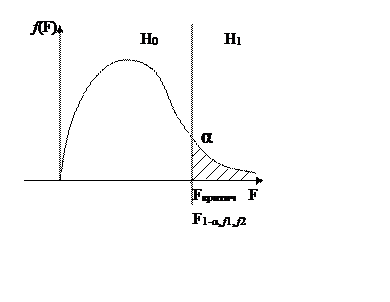
F_критич = F_{1-α, f1, f2}

Проверить нулевую гипотезу, означает найти одну границу. Для этого надо найти расчётное значение F_расч и посмотреть в какую область она попадает.

 

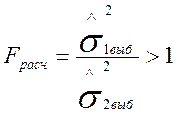
    - число степеней свободы числителя,

     - число степеней свободы знаменателя.

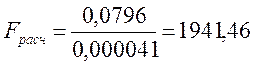
По таблице Фишера нахожу

Вывод:

Т.к.  отклоняем  нулевую гипотезу  и принимаем H1, выборочные дисперсии статистически неоднородные их различие не случайно, и принципиально у них разные параметры, принадлежат к разным генеральным совокупностям с вероятностью ошибки .

Т.к. принимаем альтернативную гипотезу, то надо данные одного эксперимента исключить из последующего эксперимента.

По указанию преподавателя не выкидываем и считаем, что обе выборки принадлежат одной совокупности

Для дальнейшего исследования берем по одному опыту из каждого эксперимента и определяем общую оценку точности данных эксперимента в виде дисперсии воспроизводимости.

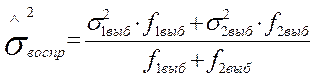
Статистический анализ регрессионной модели статики

3 направления:

-  Регрессионный анализ

-  Корреляционный анализ

-  Дисперсионный анализ

-   Основные этапы регрессионного анализа:

1.  Оценка значимости полученной модели;

2.  Оценка адекватности модели данного эксперимента.

Оценка значимости коэффициента

Все численные значения параметров  случайной модели являются случайными величинами . Они имеют нормальный закон распределения и характеризуются двумя параметрами генеральным матаматическим ожиданием и дисперсией .

, где      – генеральное математическое ожидание,

     – генеральная дисперсия.

Для каждого из коэффициентов модели необходимо выяснить равно ли нулю генеральное математическое ожидание, если , такой коэффициент называется незначимым и в нашей модели он случайно отличается от нуля. Его надо убрать из модели и модель пересчитать снова без него.

Для каждого коэффициента первой и второй модели формируется нулевая гипотеза и альтернативная.

.

,   т.е.  или .

Задаемся уровнем ошибки первого рода .

Для проверки гипотезы применяется статистика Стьюдента (t-статистика)

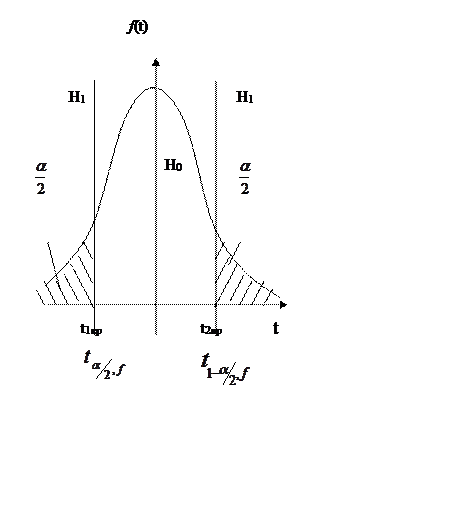
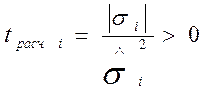
 - число степеней свободы.

f =23-4=19

Т.к.    всегда, то попасть в левую полуплоскость мы не можем. Поэтому сравниваем его только со 2-ой границей.

Если   ,  то мы отвергаем нулевую гипотезу с вероятностью ошибки 5%. Значит у данного коэффициента генеральное математическое ожидание , т.е. коэффициент значим.

Если , то  принимаем нулевую гипотезу с вероятностью ошибки 5%. Коэффициент не значим, его нужно убрать из модели.

По таблице Стьюдента:

Для первой модели t_кр1 = 2,11

Для второй модели t_кр2 = 2,10

По полученным данным лабораторной работы  уже имеем t-статистику для каждого из коэффициентов, поэтому  сравниваем уже имеющиеся данные.

Полученные результаты заношу в таблицы 1 и 2.

Для первой модели                                           для второй модели

4,710	значим
1,548	незначим
0,5192	незначим
2,132	значим
1,136	незначим
0,000122	незначим

7,940	значим
2,431	значим
0,6747	незначим
3,274	значим
0,0004212	незначим

Таблица1                                                                           Таблица2

Оценка адекватности модели данного эксперимента

Сравнивается точность модели относительно данных эксперимента и точность экспериментальных данных по параллельным опытам (по критерию Фишера).

Точность экспериментальных данных одна и та же , .

Необходимо определить точность модели , .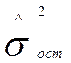

, где     N – число опытов;

l – число параметров, которые рассчитываются в данной модели.

Для первой модели:     

Для второй модели:     

Значения остаточной дисперсии для каждой модели известны и расчетных