Получение математической модели по данным пассивного эксперимента. Выборка эксперимента с параллельными опытами

сняты при одних и тех же условиях и должны иметь общую генеральную дисперсию

4. точность модели, которая оценивается ошибкой  (l_i) имеет случайный характер и все эти ошибки l₁,l₂,…,l_n тоже д.б. независимы друг от друга.

Метод МНК позволяет:

- определить несмещенное генеральное математическое ожидание,

- дает минимальное значение генеральной дисперсии.

Оценка точности экспериментальных данных

Пассивный эксперимент основан на регистрации контролируемых переменных в установившемся режиме работы . Регистрация происходит через длительные моменты времени, чтобы не было взаимного влияния измерений друг на друга.

Результаты первого эксперимента:

Х1	Х2	Y
0,893	0,09	12,266
0,934	0,086	12,476

Результаты второго эксперимента:

Х1	Х2	Y
1,181	1,268	12,973
1,253	1,245	13,312

Где  -  число параллельных опытов в первом эксперименте;

 - число степеней свободы

Где  -  число параллельных опытов во втором эксперименте;

 - число степеней свободы

Для каждого эксперимента необходимо рассчитать  и , как оценку точности.

Для обработки данных необходимо из каждого эксперимента учитывать только один выделенный опыт, поэтому из исходных данных в нашем случае нужно убрать 1 измерение из первого эксперимента и 1 измерение из второго.

Расчёт выборочного математического ожидания и дисперсии для каждого эксперимента

Выборочное мат. ожидание:

Выборочная дисперсия:

Для первого эксперимента:

m_1выб=1/2(12.266+12.476)=12.371

σ₁²_выб=1/1((12.266-12.371)²+(12.476-12.371)²)=0.02205

Для второго эксперимента:

m₂выб=1/2(13,312+12,973)=13,1425

σ₂²выб=1/1((13,312-13,1425)²+(12,973-13,1425)²)=0,0575

Оценка однородности выборочных дисперсий по критерию Фишера

При проведении параллельных опытов необходимо определить являются ли результаты измерений в первом и во втором эксперименте статистически одинаковыми (т.е. принадлежат ли эти все измерения одной генеральной совокупности, а именно имеют одни и те же генеральные параметры).

Допустим, что первый эксперимент характеризуется генеральным значением, а второй .

Выдвигается нулевая гипотеза :  полагается, что обе выборки принадлежат одной и той же генеральной совокупности, т.е. у них одно и то же значение генеральной дисперсии   . А выборочные дисперсии – это случайные оценки этой генеральной дисперсии; , поэтому выдвигается альтернативная гипотеза H₁:σ₁²>σ₂².

Задаемся уровнем ошибки первого рода .

Для проверки такой нулевой гипотезы используется статистика Фишера , которая зависит от  и двух некоторых показателей степеней свободы  и . Причём всегда .

Кривая распределения Фишера.

 

                                    

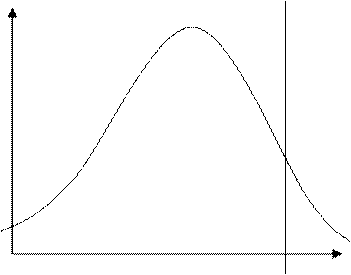_,f1,f2    S

t_1-α, _f1,f2

Проверить нулевую гипотезу, означает найти одну границу. Для этого надо найти расчётное значение  и посмотреть в какую область попадём.

  причём  - число степеней свободы числителя, а  - число степеней свободы знаменателя.

F_расч=0,0575/0,02205=2,61

По таблице нахожу критическое значение F_кр=19,00.

Получаю, что F_расч < F_кр, т.е. попадаю в область нулевой гипотезы. Вывод:  выборочные дисперсии статистически однородны, их различие случайно и генеральное значение одинаково.

Оценка значимости полученных коэффициентов модели

Все численные значения коэффициентов модели – случайные величины, они имеют нормальный закон распределения bi → N(β_i,σ_i²), где β_i – генеральное мат. Ожидание.

Y=b₀+Σb_iX_i+Σb_iiX_i²+Σb_ijX_iX_j

Для каждого b_i модели нужно определить: равно ли нулю генеральное мат. ожидание.

Если β_i =0, такой коэффициент называется незначительным и он случайно отличается от 0 , его надо из модели убрать, модель пересчитать снова.

Для каждого кожффициента модели формулируются нулевая и альтернативная гипотизы:

Н₀: β_i = 0

Н₁: β_i ≠ 0→ β_i>0

→ β_i<0

Задаемся уравнением ошибки 1-го рода:α = 0,05

Применяется Т-статистика.

t_расчi =(/b_i/:σ_i²)>0

Т.к. t_расчi>0,попасть в левую часть плоскости не можем, сравниваем

t_расчi с t_кр, отвергаем Н₀, значит β_i≠0, коэффициент значим, в противном случае принимаем Н₀, коэффициент незначим.

Для полной модели:

	Коэф. модели	Т-статистика	tкр	значимость
1	18,66	4,013	2,11	зн.
2	3,444	1,161	2,11	не зн.
3	6,393	1,574	2,11	не зн.
4	1,129	0,3611	2,11	не зн.
5	2,198	0,6137	2,11	не зн.
6	0,0001051	0,00002705	2,11	не зн.

Для выборочной модели:

	Коэф. модели	Т-статистика	tкр	значимость
1	16,97	5,683	2,09	зн.
2	0,3333	0,1673	2,09	не зн.
3	5,499	1,96	2,09	не зн.
4	0,0003328	0,0001348	2,09	не зн.

Расчёт дисперсии воспроизводимости

Сравнивается погрешность модели относительно данных эксперимента и точность экспериментальных данных по параллельным опытам.

Точность экспериментальных данных оценивается дисперсией воспроизводимости  и числом степеней свободы .

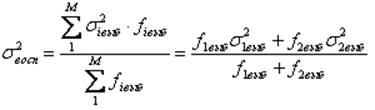
=(1*0,02205+1*0,0575)/(1+1)= 0.0398

Точность модели оценивается остаточной дисперсией:

значения известны из расчетных данных.

Для первой модели (полной):σ₁²_ост=146.8

Для второй модели (выборочной): σ₂²_ост=76,83.

Генеральная дисперсия экспериментальных данных σ_y²  и генеральная дисперсия модели .

Полная модель:

Нулевая гипотеза  .

Альтернативная гипотеза : , тогда Н₁: .

Задаемся уровнем ошибки первого рода .

Для проверки такой нулевой гипотезы используем статистику Фишера.    

Проверить нулевую гипотезу, значит найти одну границу. Для этого надо найти расчётное значение  и посмотреть в какую область попадём.

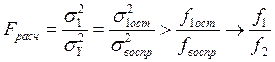  причём  - число степеней свободы числителя, а  - число степеней свободы знаменателя.

F_расч=146.8/0.0398=3688.4

По таблице критическое значение F_кр= 19,43.

Вывод:F_расч > F_кр . Модель неадекватна экспериментальным данным, отвергаю H₀, предлагаю