Имитационное моделирование линейной дискретной одноконтурной системы

Министерство  образования  Российской Федерации

Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров

Кафедра АТЭП

Лабораторная работа:

Имитационное моделирование линейной дискретной одноконтурной системы.

Часть I.  Изучение «Автоматизированной системы имитационного моделирования» - ASIM_LIN

Выполнил:                                                                                студенты группы 544                                                                                           

    

Проверил:                                                                      

Санкт-Петербург

2008г.

В данной лабораторной работе рассматривается система автоматического управления концентрации бумажной массы по заданным критериям качества.

Цель: изучение структуры и возможностей стандартного программного обеспечения   (ASIM) решения ряда вопросов синтеза и анализа линейных одноконтурных дискретных систем регулирования, использующих  амплитудно-импульсную модуляцию сигналов.

Исходные данные:

1. Объект регулирования:

Канал управления: «Изменение расхода оборотной воды - изменение концентрации массы»  

K₀*exp(-Tau*P)

Математическая модель:         W_об(P) =

1+T*P           ,            где  T   =  70      [c]-постоянная времени объекта по каналу управления;

K₀ = -0,015 [%конц./л/с]-коэффициент передачи объекта по каналу управления;

Tau = 10      [c]-запаздывание по каналу управления.

2. Датчик с преобразователем:

W_дат(P) = К_дат,          где К_дат = 0,2 [кг/см²возд/%конц]

3. Регулирующий блок:

K₁z-K₂

Дискретный регулятор Д(z) =                             , [1]  ,   где К₁ и К₂-настройки дискретного ПИ-регулятора.                                        z-1

Исполнительный механизм  W_им(P) = K_им  , где  K_им = 125 [%откр.клап./кг/см²возд.]

Регулирующий орган   W_ро(P) = K_ро  ,где К_ро = 0,3 [л/с/%откр.клап.]

4.Канал возмущения по управляемому входу объекта: «изменение уровня массы в массном бассейне -изменение расходом массы»

K_f2

Математическая модель:         W_f2(P) =

1+T_f2*P                  , где  K_f2 = 1,3[л/с/см]-коэффициент передачи канала возмущения;

T_f2 = 40[с]-постоянная времени канала возмущения.

5. Период дискретности работы системы:

T₀ = 5 [c]

6.Модели типовых входных воздействий:

Изменение задающего воздействия  Δg(t) [%конц.]:

Δg(t)=a*1[t] ,где а = 0,4.

Изменение уровня массы в бассейне Δη₂(t) [см]:

Δη₂(t)=a*1[t] ,где а = 8

Δη₂(t)=a*exp(α*t) ,где а = 5 и α = 0,001

Δη₂(t)=a*sinw*t , где а = 3 и w = 0,002.

Изменение концентрации оборотной воды Δη₁(t)[ [%концен]:

Δη₁(t)=a*1[t] ,где а = 1

Δη₁(t)=a*exp(α-t) ,где а = 2,7 и α = 0,01

Δη₁(t)=a*sinw*t , где а = 1,7 и w = 0,05

7. Требования к качеству управления:

·  Точность поддержания значения концентрации: Е = ±0,15 [%конц.];

·  Степень колебательности: m = 0,9.

Расчет конечного значения регулируемого параметра для варьируемых значений задающего воздействия.

Передаточная функция для замкнутой дискретной системы:

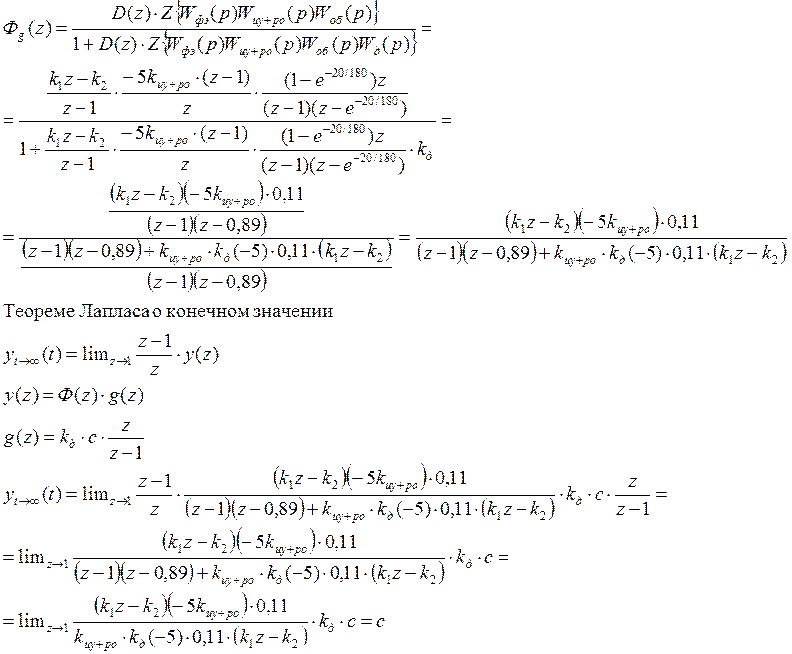
Оценка качества систем управления

1. Оценка точности:

Задача работы системы управления заключается в том, чтобы в любой момент времени Δy(t)=Δg(t).

Но это равенство нарушается вследствие наличия в системе статической ошибки ΔE(t).

Для нахождения конечного значения статической ошибки и для канала управления ,и для канала возмущения используем формулу:        ΔE∞ = Δg∞-Δy∞ , где Δg∞-изменение задающего воздействия;

Δy∞-новое установившееся значение.

Оценка качества по каналу управления и по каналу возмущения будет разная, так как мы оцениваем их по-разному.

2. Запас устойчивости системы управления:

Запас устойчивости определяет степень удаленности системы от колебательной границы.

По каналу управления:

Δy_мах- Δy∞

Перерегулирование:  σ =                             [%] , где  Δy_мах - максимальное значение;

Δy∞                                Δy∞ - новое установившееся состояние.

у_1мах - у_2мах

Затухание  за период:  ξ =                              [%] , где   y_1мах -первое максимальное значение;

у_1мах                                            y_2мах - второе максимальное значение;

По каналу возмущения:

y₂

Перерегулирование:  σ =                        [%] ,    где      y₂-второе максимальное значение;

y₃                                    y₃-третье максимальное значение.

у₁ – у₃

Затухание  за период:  ξ =                              [%] ,     где   y₁-первое максимальное значение;

у                                        y₃-третье максимальное значение.

3.Быстродействие:

По каналу управления:

Быстродействие системы определяется временем от момента подачи входного воздействия до момента, когда регулируемая величина будет равна заданному значению. Теоретически это время равно бесконечности. Поэтому время прекращения движения необходимо выбрать до момента, когда отклонение выходной величины от ее нового установившегося значения  станет меньше некоторой определенной малой величины (Δ=3-5% от Δy∞).

Δ=׀Δy∞- Δy(t) ׀=5 % от Δy∞.

По каналу возмущения:

По каналу возмущения за величину Δ берут величину допустимой ошибки