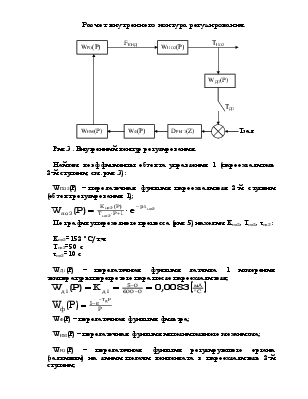
Расчет внутреннего контура регулирования. Внутренний контур регулирования. Дискретная передаточная функция НЧС с учетом выражения

Расчет внутреннего контура регулирования.

 

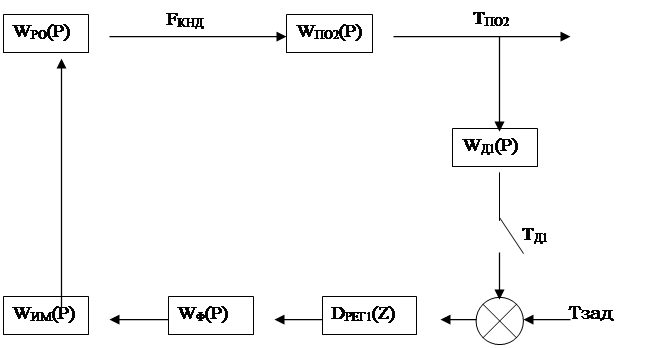Рис.3. Внутренний контур регулирования.

Найдем коэффициенты объекта управления 1 (пароохладитель 2-й ступени, см. рис.3):

W_ПО2(P) – передаточная функция пароохладителя 2-й ступени (объект регулирования 1);

По графику переходного процесса (рис.5) находим К_по2, Т_по2, τ_по2:

К_по2=152 ºС/т_/ч

Т_по2=50 с

τ_по2=10 с

W_Д1(Р) – передаточная функция датчика 1 измерения температуры перегретого пара после пароохладителя;

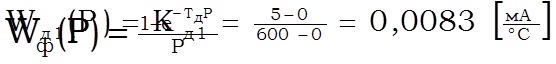W_Ф(Р) – передаточная функция фильтра;

W_ИМ(Р) – передаточная функция исполнительного механизма;

W_РО(Р) – передаточная функция регулирующего органа (задвижки) на линии подачи конденсата в пароохладитель 2-й ступени;

Для исполнительного механизма и регулирующего органа объединим передаточные функции W_ИМ(Р) и W_РО(Р) в одну передаточную функцию W_ИМ+РО(Р):

D_РЕГ1(Z) – передаточная функция регулятора 1:

Для регулирования внутреннего контура применяем ПИ-закон регулирования. Это позволит увеличить точность регулирования, уменьшить время отработки задающего воздействия, свести статическую ошибку к 0 (нулю).

Расчет производится по следующим уравнениям [9]:

определим дискретную передаточную функцию непрерывной части (НЧС) цифровой САУ:

D_НЧС(Z)=Z{W_Ф(P)·W_ИУ(Р) ·W_ИМ+РО(Р) ·W_ПО2(Р) ·W_Д(Р)}          (1)

Передаточную функцию формирующего элемента объединяем с передаточной функцией объекта управления:

где m= τ_по2/Т_д.

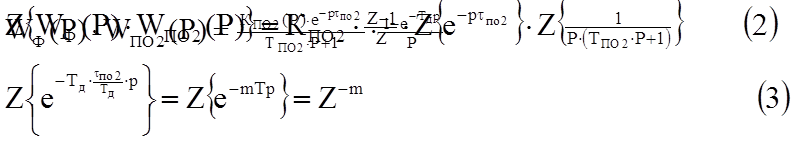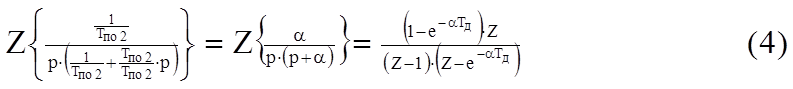где α=1/Т_ПО2.

После подстановки выражений (3) и (4) в выражение (2), получим:

После замены

получим окончательно:

Дискретная передаточная функция НЧС с учетом выражения (6) будет:

Известно, что дискретная передаточная функция цифрового регулятора с ПИ-законом регулирования имеет следующее выражение: где С1 и С2 – параметры настройки цифрового ПИ-алгоритма управления.

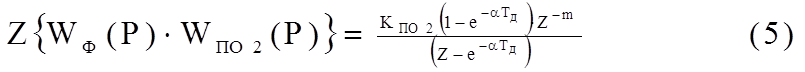Дискретная передаточная функция цифрового регулятора с ПИ- алгоритмом управления будет следующая:

D(Z)=D_НЧС(Z)·D_P(Z)                                                                        (9)

После подстановки и ряда преобразований получим:

где К_С=К_ПО2·К_Д·К_ИУ.

Заменив в выражении (10) К_С·(1-d)=К_D, получим:

С помощью метода расширенных АФЧХ разомкнутой САУ производим построение границы колебательной устойчивости и линии равной колебательности.

Полагаем, что 1+D(Z) = 0.

После некоторых преобразований, группировки и решения системы относительно С1 и С2, получим уравнения для их нахождения  [9].

Используя программу В1 рассчитываем на ПЭВМ границу колебательной устойчивости (М=0) и линию равной колебательности (М=0,8) (таблица 6 и 7).

а) определение границы колебательной устойчивости (М=0) – см. рис.7.

б) определение линии равной колебательности (М=0,8) – см. рис.8: находим оптимальные настройки регулятора 1:

С1=0,849 ; С2=0,640 .

Используя программу В2 [9] производим построение переходного процесса по управляющему воздействию (единичному) (см. рис.9) при разных настройках С1 и С2:

а) при С1=0,849 и С2=0,640

перерегулирование составляет 23%, что в переводе на градусы ºС =2,3 ºС (таб.8).

б) при других настройках: С1=0,801 и С2=0,677

перерегулирование составляет 3,4%, что в переводе на градусы ºС =0,3 ºС (таб.9).

в) С1=0,821 и С2=0,601

перерегулирование составляет 26%, что в переводе на градусы ºС =2,6 ºС (таб.10).

При построении графика переходного процесса с разными настройками С1 и С2 (рис.9) видно, что минимальное перерегулирование будет при С1=0,801 и С2=0,677 (не более 3,4%).